11 A Game of Probability
Most people are familiar with the game of dice. If played with a fair set of dice then each player has an equal chance of winning. Over a sufficient number of throws, the expected outcome is zero, assuming there are no costs to playing the game such as a casino operator’s cut. There is no strategy that can be employed fairly to alter this outcome – such as favouring one hand over the other, or saying something during the throw, or insisting on going first or second – so the outcome of each throw is randomly distributed as is the outcome of each game. If a player wins it is purely a matter of luck and so their performance in one session provides no insight in relation to their likely performance in the next session or over the longer term.
At first glance, trading in a market such as Forex or commodity futures might appear to be a bit like this. After all, any security will eventually either go up or go down and so, leaving aside the market maker’s commission, the expected outcome would appear to be zero, in the absence of a strategy. In fact, this is not the case for a private trader with limited funds because of the importance of controlling risk. This requirement actually moves the odds against you on any trade, even though it increases the long term possibility of success.
A strategy makes all the difference – even in a game of dice once we change any of the underlying rules. A story is told that Warren Buffet once challenged Bill Gates to a game of dice{1}. When he looked at the 3 pairs of dice offered by Buffet, Gates noticed that the numbering on each had been changed from the usual 1 to 6 with opposite sides equaling 7, but Buffet assured him that the dice were otherwise fair and that Gates could choose which pair he wished to use. Gates hesitated, knowing that Buffet liked to play games but that he seldom entered a game, anymore than he would enter an investment, without a strategy that would tilt the pay-off in his favour. However, he also knew that Buffet would not lie to him about the fact that the dice where normal other than the numbering that he could see.
There were 3 pairs of dice which we will label A, B, and C. Each die in each pair had the same numbering. The numbering on the dice was as follows. Set A had 2 sides with the number 5 on each and 4 sides with the number 2 on each. Set B had 4 sides with the number 4 on each and 2 sides with the number 1 on each. Set C had the number 3 on each side. The dice appear equal since the sum of all sides on each is 18, irrespective of the pair that is chosen.
Gates considered the situation for a while and said that he would be happy to play the game with the sets of dice Buffet offered but only if Buffet made his choice of which set he would play with first, and only then would he choose his set. Buffet decided not to accept the revised rule.
So, what was going on here? If Gates was willing to play he must have considered that the game was not inherently loaded against him, but why would he insist on giving up the opportunity to choose between the 3 sets? After all, if one set was preferable then surely Buffet would know this and would gain an advantage by having the first choice and using this set. This would leave Gates with a choice between only 2 inferior sets. But then Buffet also refused this apparent advantage.
To see what is going on here we need to calculate the percentage of games we should expect to win using each set of dice over a series of games. The data we need are shown below in Table 1. What emerges is that these sets of dice were what mathematicians would describe as ‘non-transitive’, in other words, no set beats both of the other two sets.
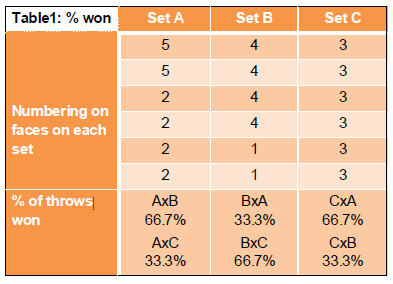
For example, let’s say that Gates did not spot the implications of the numbering on the dice and had agreed to go first and chose set B. Buffet would immediately know to choose set A and so would win 4 out of 6 times the dice are thrown i.e. 66.7% of the time. Seeing this and thinking he had learned something, Gates would want to play again and this time would probably take set A. Buffet would immediately choose set C and would easily win the game since C beats A 2 times out of 3, or 66.7% of the time. If he still had not copped on, Gates might decide to try his luck with set C. Buffet would then simply choose set B and again win 66.7% of the time.
So, no matter which set the first player chooses in this game the second player will always win. Agreeing to go first, while seeming to give you a better choice, is like trying to play rock-paper-scissors and showing your hand first. By agreeing to go first you are not gaining an advantage but, rather, you are providing the key piece of information to your competitor that they require to make their strategy successful.
This type of outcome is also often seen in business when the first firm to bring a new, genuinely innovative product to market does not get the greatest market share. Instead, this often goes to a second firm which mostly copies the first, usually with some minor innovations, but learns from any mistakes made by the first firm thereby greatly reducing its risks and, therefore, its costs.
So, what has this to do with trading? For simplicity we will now assume that the game is played by each player only throwing 1 die each time from the set they have chosen. Let’s also assume that rather than the simple win/lose outcome that is used in a game of dice, you still win if you throw a larger number than the other player, but your winnings are equal to the number you throw. If you throw a smaller number than your opponent then your loss is equal to the number thrown by the other player. For example, if you are playing with a die from set A and you throw a 2 while your opponent is playing with set B and throws a 1, then you win 2 points (or Euro or $). However, if the other player throws a 4, then you lose 4.
Consider the information shown in Table 2. It summarises the outcomes that would be produced for all possible decisions by the players in relation to which set they wish to use, assuming that they play 36 throws each and that each possible outcome appears just once.
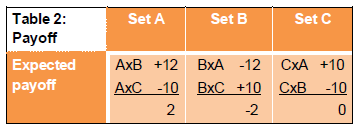
The relative ordering is unaffected so Buffet’s attempted trick on Gates would still work i.e. B beats C and A beats B, but C beats A. However, only A has a positive payoff overall. Importantly, this arises because set A’s potential losses are smaller than the potential gains, while the reverse is true for set B.
Obviously, the series of numbering on the dice as described here was chosen to achieve this outcome and is only one of many options that would bring about non-transitive sets of dice. However, it illustrates a very important lesson in relation to trading and the correct strategy to employ.
The set of dice C with the number 3 on every side can be considered as equivalent to a risk-free investment on every throw. There is no doubt about the outcome of the throw, you will get a 3, and while some alternative investment might have provided a larger return on any particular throw, they win exactly 50% of the time with 24 wins against A, out of the 36 possible outcomes, and 12 against B.
Set B is akin to the strategies that are employed by hedge funds, among others. Compared to risk free investments they win more often in terms of returns. Against A they will win on 16 of the 36 possible outcomes and against C they will win on 24 of the 36 possible outcomes giving a total of 40. i.e. 55.6% of the time. However, many of the wins are small and there are some relatively large losses. But the important issue for these hedge funds is that most of the time they are providing superior returns and then they need only to ensure that the losses are rare and do not destroy their capital base.
Set A looks unpromising in terms of the number of trades that are won. It wins 20 out of 36 against B and only 12 against C for a total of 32 i.e. it wins only 44.4% of the throws. And yet, because the losing trades are relatively small compared to the losing trades, this strategy produces a positive payoff.
There are three very important lessons here, apart from not playing dice with Warren Buffet, or Bill Gates for that matter. The first is that the individual trader, particularly if they are trading on margin, must approach the market with a strategy that will shift the odds in their favour. They must know and understand their strategy and must follow its rules.
Second, the trader must focus on controlling losses. Once in a trade, the only thing you can control is exposure to risk, the ultimate control being to exit the trade and eliminate the risk. So, your only strategy is to manage the trade in terms of its associated risk. As the example of the dice shows, this is a vital element in a strategy where you have no control over the outcome, be it how the dice will land or where the market will go.
Third, in assessing any strategy, whether during the development stage or when it is employed and records are kept and monitored, the percentage of wins is not the only, and perhaps not even the most important, measure of performance. Set A above had the lowest expected number of wins, but it represented the only strategy that provided a positive pay-off. In trading, the ratio of wins to losers is the key.
This final point might not be as simple for an active trader to monitor as might first appear. For example, the trader might enter and get stopped out for a loss on one currency pair and leave it at that. He or she might then enter a trade in a different pair and exit with a small profit for some good reason and re-enter later. This can happen a number of times over the course of a trend. In effect, all these trades are the one trade so the comparison is between the cumulative gains on these trades and the loss initially. This can be very difficult to monitor so the best approach is to set the stop and target before entering.
A stop must always be an absolute: the trade ends if it is hit. The target is somewhat more notional in the sense that it represents a level that, it can reasonably be argued, the security has a good chance of reaching, but it does not mean that the trade will be kept opened until this level is reached. It can also be extended. A trader will very often decide to exit and re-enter before this target is reached. However, by setting both the stop and the target at the same time and using a similar type of analysis, the trader can ensure that the potential gain in any tradable set-up is a sufficient multiple of the appropriate risk before entering the trade.





