Chapter 6
Fruitful methods
6.1
Return values
Some of the methods we have used, like the Math functions, produce results.
That is, the effect of invoking the method is to generate a new value, which
we usually assign to a variable or use as part of an expression. For example:
double e = Math.exp(1.0);
double height = radius * Math.sin(angle);
But so far all our methods have been void; that is, methods that return no
value. When you invoke a void method, it is typically on a line by itself, with
no assignment:
countdown(3);
nLines(3);
In this chapter we write methods that return things, which I call fruitful
methods. The first example is area, which takes a double as a parameter,
and returns the area of a circle with the given radius:
public static double area(double radius) {
double area = Math.PI * radius * radius;
return area;
}
The first thing you should notice is that the beginning of the method defi-
nition is different. Instead of public static void, which indicates a void
56
Chapter 6. Fruitful methods
method, we see public static double, which means that the return value
from this method is a double. I still haven’t explained what public static
means, but be patient.
The last line is a new form of the return statement that includes a return
value. This statement means, “return immediately from this method and
use the following expression as a return value.” The expression you provide
can be arbitrarily complicated, so we could have written this method more
concisely:
public static double area(double radius) {
return Math.PI * radius * radius;
}
On the other hand, temporary variables like area often make debugging
easier. In either case, the type of the expression in the return statement must
match the return type of the method. In other words, when you declare that
the return type is double, you are making a promise that this method will
eventually produce a double. If you try to return with no expression, or an
expression with the wrong type, the compiler will take you to task.
Sometimes it is useful to have multiple return statements, one in each branch
of a conditional:
public static double absoluteValue(double x) {
if (x < 0) {
return -x;
} else {
return x;
}
}
Since these return statements are in an alternative conditional, only one will
be executed. Although it is legal to have more than one return statement
in a method, you should keep in mind that as soon as one is executed, the
method terminates without executing any subsequent statements.
Code that appears after a return statement, or any place else where it can
never be executed, is called dead code. Some compilers warn you if part of
your code is dead.
If you put return statements inside a conditional, then you have to guarantee
that every possible path through the program hits a return statement. For
6.2. Program development
57
example:
public static double absoluteValue(double x) {
if (x < 0) {
return -x;
} else if (x > 0) {
return x;
}
// WRONG!!
}
This program is not legal because if x is 0, neither condition is true and the
method ends without hitting a return statement. A typical compiler message
would be “return statement required in absoluteValue,” which is a confusing
message since there are already two of them.
6.2
Program development
At this point you should be able to look at complete Java methods and tell
what they do. But it may not be clear yet how to go about writing them. I
am going to suggest a method called incremental development.
As an example, imagine you want to find the distance between two points,
given by the coordinates (x1, y1) and (x2, y2). By the usual definition,
distance =
(x2 − x1)2 + (y2 − y1)2
(6.1)
The first step is to consider what a distance method should look like in
Java. In other words, what are the inputs (parameters) and what is the
output (return value)?
In this case, the two points are the parameters, and it is natural to represent
them using four doubles, although we will see later that there is a Point
object in Java that we could use. The return value is the distance, which
will have type double.
Already we can write an outline of the method:
public static double distance
(double x1, double y1, double x2, double y2) {
return 0.0;
}
58
Chapter 6. Fruitful methods
The statement return 0.0; is a place-keeper that is necessary to compile the
program. Obviously, at this stage the program doesn’t do anything useful,
but it is worthwhile to try compiling it so we can identify any syntax errors
before we add more code.
To test the new method, we have to invoke it with sample values. Somewhere
in main I would add:
double dist = distance(1.0, 2.0, 4.0, 6.0);
I chose these values so that the horizontal distance is 3 and the vertical dis-
tance is 4; that way, the result will be 5 (the hypotenuse of a 3-4-5 triangle).
When you are testing a method, it is useful to know the right answer.
Once we have checked the syntax of the method definition, we can start
adding lines of code one at a time. After each incremental change, we recom-
pile and run the program. If there is an error at any point, we have a good
idea where to look: in the last line we added.
The next step is to find the differences x2 − x1 and y2 − y1. I store those
values in temporary variables named dx and dy.
public static double distance
(double x1, double y1, double x2, double y2) {
double dx = x2 - x1;
double dy = y2 - y1;
System.out.println("dx is " + dx);
System.out.println("dy is " + dy);
return 0.0;
}
I added print statements so we can check the intermediate values before
proceeding. They should be 3.0 and 4.0.
When the method is finished I remove the print statements. Code like that
is called scaffolding, because it is helpful for building the program, but it
is not part of the final product.
The next step is to square dx and dy. We could use the Math.pow method,
but it is simpler to multiply each term by itself.
public static double distance
(double x1, double y1, double x2, double y2) {
6.2. Program development
59
double dx = x2 - x1;
double dy = y2 - y1;
double dsquared = dx*dx + dy*dy;
System.out.println("dsquared is " + dsquared);
return 0.0;
}
Again, I would compile and run the program at this stage and check the
intermediate value (which should be 25.0).
Finally, we can use Math.sqrt to compute and return the result.
public static double distance
(double x1, double y1, double x2, double y2) {
double dx = x2 - x1;
double dy = y2 - y1;
double dsquared = dx*dx + dy*dy;
double result = Math.sqrt(dsquared);
return result;
}
In main, we can print and check the value of the result.
As you gain more experience programming, you might write and debug more
than one line at a time. Nevertheless, incremental development can save you
a lot of time.
The key aspects of the process are:
❼ Start with a working program and make small, incremental changes.
At any point, if there is an error, you will know exactly where it is.
❼ Use temporary variables to hold intermediate values so you can print
and check them.
❼ Once the program is working, you can remove scaffolding and consoli-
date multiple statements into compound expressions, but only if it does
not make the program difficult to read.
60
Chapter 6. Fruitful methods
6.3
Composition
Once you define a new method, you can use it as part of an expression, and
you can build new methods using existing methods. For example, what if
someone gave you two points, the center of the circle and a point on the
perimeter, and asked for the area of the circle?
Let’s say the center point is stored in the variables xc and yc, and the
perimeter point is in xp and yp. The first step is to find the radius of the
circle, which is the distance between the two points. Fortunately, we have a
method, distance that does that.
double radius = distance(xc, yc, xp, yp);
The second step is to find the area of a circle with that radius, and return it.
double area = area(radius);
return area;
Wrapping that all up in a method, we get:
public static double circleArea
(double xc, double yc, double xp, double yp) {
double radius = distance(xc, yc, xp, yp);
double area = area(radius);
return area;
}
The temporary variables radius and area are useful for development and
debugging, but once the program is working we can make it more concise by
composing the method invocations:
public static double circleArea
(double xc, double yc, double xp, double yp) {
return area(distance(xc, yc, xp, yp));
}
6.4
Overloading
You might have noticed that circleArea and area perform similar
functions—finding the area of a circle—but take different parameters. For
area, we have to provide the radius; for circleArea we provide two points.
6.4. Overloading
61
If two methods do the same thing, it is natural to give them the same name.
Having more than one method with the same name, which is called over-
loading, is legal in Java as long as each version takes different parameters.
So we could rename circleArea:
public static double area
(double x1, double y1, double x2, double y2) {
return area(distance(xc, yc, xp, yp));
}
When you invoke an overloaded method, Java knows which version you want
by looking at the arguments that you provide. If you write:
double x = area(3.0);
Java goes looking for a method named area that takes one double as an
argument, and so it uses the first version, which interprets the argument as
a radius. If you write:
double x = area(1.0, 2.0, 4.0, 6.0);
Java uses the second version of area. And notice that the second version of
area actually invokes the first.
Many Java methods are overloaded, meaning that there are different versions
that accept different numbers or types of parameters. For example, there are
versions of print and println that accept a single parameter of any type.
In the Math class, there is a version of abs that works on doubles, and there
is also a version for ints.
Although overloading is a useful feature, it should be used with caution. You
might get yourself nicely confused if you are trying to debug one version of
a method while accidently invoking a different one.
And that reminds me of one of the cardinal rules of debugging: make sure
that the version of the program you are looking at is the version
of the program that is running!
Some day you may find yourself making one change after another in your
program, and seeing the same thing every time you run it. This is a warning
sign that you are not running the version of the program you think you are.
To check, add a print statement (it doesn’t matter what you print) and
make sure the behavior of the program changes accordingly.
62
Chapter 6. Fruitful methods
6.5
Boolean expressions
Most of the operations we have seen produce results that are the same type
as their operands. For example, the + operator takes two ints and produces
an int, or two doubles and produces a double, etc.
The exceptions we have seen are the relational operators, which compare
ints and floats and return either true or false. true and false are special
values in Java, and together they make up a type called boolean. You might
recall that when I defined a type, I said it was a set of values. In the case of
ints, doubles and Strings, those sets are pretty big. For booleans, not so
big.
Boolean expressions and variables work just like other types of expressions
and variables:
boolean bob;
bob = true;
boolean testResult = false;
The first example is a simple variable declaration; the second example is an
assignment, and the third example is an initialization.
The values true and false are keywords in Java, so they may appear in a
different color, depending on your development environment.
The result of a conditional operator is a boolean, so you can store the result
of a comparison in a variable:
boolean evenFlag = (n%2 == 0);
// true if n is even
boolean positiveFlag = (x > 0);
// true if x is positive
and then use it as part of a conditional statement later:
if (evenFlag) {
System.out.println("n was even when I checked it");
}
A variable used in this way is called a flag because it flags the presence or
absence of some condition.
6.6. Logical operators
63
6.6
Logical operators
There are three logical operators in Java: AND, OR and NOT, which are
denoted by the symbols &&, || and !. The semantics of these operators is
similar to their meaning in English. For example x > 0 && x < 10 is true
only if x is greater than zero AND less than 10.
evenFlag || n%3 == 0 is true if either of the conditions is true, that is, if
evenFlag is true OR the number is divisible by 3.
Finally, the NOT operator inverts a boolean expression, so !evenFlag is true
if evenFlag is false—if the number is odd.
Logical operators can simplify nested conditional statements. For example,
can you re-write this code using a single conditional?
if (x > 0) {
if (x < 10) {
System.out.println("x is a positive single digit.");
}
}
6.7
Boolean methods
Methods can return boolean values just like any other type, which is often
convenient for hiding tests inside methods. For example:
public static boolean isSingleDigit(int x) {
if (x >= 0 && x < 10) {
return true;
} else {
return false;
}
}
The name of this method is isSingleDigit. It is common to give boolean
methods names that sound like yes/no questions. The return type is boolean,
which means that every return statement has to provide a boolean expression.
The code itself is straightforward, although it is longer than it needs to be.
Remember that the expression x >= 0 && x < 10 has type boolean, so there
64
Chapter 6. Fruitful methods
is nothing wrong with returning it directly and avoiding the if statement
altogether:
public static boolean isSingleDigit(int x) {
return (x >= 0 && x < 10);
}
In main you can invoke this method in the usual ways:
boolean bigFlag = !isSingleDigit(17);
System.out.println(isSingleDigit(2));
The first line sets bigFlag to true only if 17 is not a single-digit number.
The second line prints true because 2 is a single-digit number.
The most common use of boolean methods is inside conditional statements
if (isSingleDigit(x)) {
System.out.println("x is little");
} else {
System.out.println("x is big");
}
6.8
More recursion
Now that we have methods that return values, we have a Turing com-
plete programming language, which means that we can compute anything
computable, for any reasonable definition of “computable.”
This idea was developed by Alonzo Church and Alan Turing, so it is known
as the Church-Turing thesis. You can read more about it at http://en.
wikipedia.org/wiki/Turing_thesis.
To give you an idea of what you can do with the tools we have learned,
let’s look at some methods for evaluating recursively-defined mathematical
functions. A recursive definition is similar to a circular definition, in the
sense that the definition contains a reference to the thing being defined. A
truly circular definition is not very useful:
recursive: an adjective used to describe a method that is recursive.
6.8. More recursion
65
If you saw that definition in the dictionary, you might be annoyed. On the
other hand, if you looked up the definition of the mathematical function
factorial, you might get something like:
0! = 1
n! = n · (n − 1)!
(Factorial is usually denoted with the symbol !, which is not to be confused
with the logical operator ! which means NOT.) This definition says that the
factorial of 0 is 1, and the factorial of any other value, n, is n multiplied by
the factorial of n − 1. So 3! is 3 times 2!, which is 2 times 1!, which is 1
times 0!. Putting it all together, we get 3! equal to 3 times 2 times 1 times
1, which is 6.
If you can write a recursive definition of something, you can usually write a
Java method to evaluate it. The first step is to decide what the parameters
are and what the return type is. Since factorial is defined for integers, the
method takes an integer as a parameter and returns an integer:
public static int factorial(int n) {
}
If the argument happens to be zero, return 1:
public static int factorial(int n) {
if (n == 0) {
return 1;
}
}
That’s the base case.
Otherwise, and this is the interesting part, we have to make a recursive call
to find the factorial of n − 1, and then multiply it by n.
public static int factorial(int n) {
if (n == 0) {
return 1;
} else {
int recurse = factorial(n-1);
int result = n * recurse;
return result;
66
Chapter 6. Fruitful methods
}
}
The flow of execution for this program is similar to countdown from Sec-
tion 4.8. If we invoke factorial with the value 3:
Since 3 is not zero, we take the second branch and calculate the factorial of
n − 1...
Since 2 is not zero, we take the second branch and calculate the
factorial of n − 1...
Since 1 is not zero, we take the second branch and
calculate the factorial of n − 1...
Since 0 is zero, we take the first branch and re-
turn the value 1 immediately without making
any more recursive invocations.
The return value (1) gets multiplied by n, which is 1,
and the result is returned.
The return value (1) gets multiplied by n, which is 2, and the
result is returned.
The return value (2) gets multiplied by n, which is 3, and the result, 6, is
returned to main, or whoever invoked factorial(3).
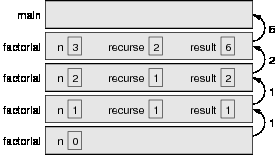
Here is what the stack diagram looks like for this sequence of method invo-
cations:
6.9. Leap of faith
67
The return values are shown being passed back up the stack.
Notice that in the last frame recurse and result do not exist because when
n=0 the branch that creates them does not execute.
6.9
Leap of faith
Following the flow of execution is one way to read programs it can quickly
become labarynthine. An alternative is what I call the “leap of faith.” When
you come to a method invocation, instead of following the flow of execution,
you assume that the method works correctly and returns the appropriate
value.
In fact, you are already practicing this leap of faith when you use Java
methods. When you invoke Math.cos or System.out.println, you don’t
examine the implementations of those methods. You just assume that they
work.
You can apply the same logic to your own methods. For example, in Sec-
tion 6.7 we wrote a method called isSingleDigit that determines whether
a number is between 0 and 9. Once we convince ourselves that this method
is correct—by testing and examination of the code—we can use the method
without ever looking at the code again.
The same is true of recursive programs.
When you get to the recursive
invocation, instead of following the flow of execution, you should assume
that the recursive invocation works, and then ask yourself, “Assuming that
I can find the factorial of n − 1, can I compute the factorial of n?” Yes, you
can, by multiplying by n.
Of course, it is strange to assume that the method works correctly when you
have not even finished writing it, but that’s why it’s called a leap of faith!
68
Chapter 6. Fruitful methods
6.10
One more example
The second most common example of a recursively-defined mathematical
function is fibonacci, which has the following definition:
f ibonacci(0) = 1
f ibonacci(1) = 1
f ibonacci(n) = f ibonacci(n − 1) + f ibonacci(n − 2);
Translated into Java, this is
public static int fibonacci(int n) {
if (n == 0 || n == 1) {
return 1;
} else {
return fibonacci(n-1) + fibonacci(n-2);
}
}
If you try to follow the flow of execution here, even for small values of n,
your head explodes. But according to the leap of faith, if we assume that
the two recursive invocations work correctly, then it is clear that we get the
right result by adding them together.
6.11
Glossary
return type: The part of a method declaration that indicates what type of
value the method returns.
return value: The value provided as the result of a method invocation.
dead code: Part of a program that can never be executed, often because it
appears after a return statement.
scaffolding: Code that is used during program development but is not part
of the final version.
void: A special return type that indicates a void method; that is, one that
does not return a value.
6.12. Exercises
69
overloading: Having more than one method with the same name but differ-
ent parameters. When you invoke an overloaded method, Java knows
which version to use by looking at the arguments you provide.
boolean: A type of variable that can contain only the two values true and
false.
flag: A variable(usually boolean) that records a condition or status infor-
mation.
conditional operator: An operator that compares two values and produces
a boolean that indicates the relationship between the operands.
logical operator: An operator that combines boolean values and produces
boolean values.
6.12
Exercises
Exercise 6.1. Write a method named isDivisible that takes two integers,
n and m and that returns true if n is divisible by m and false otherwise.
Exercise 6.2. Many computations can be expressed concisely using the “mul-
tadd” operation, which takes three operands and computes a*b + c. Some
processors even provid




