Chapter 9
Mutable objects
9.1
Points and Rectangles
Strings are objects, but they are atypical objects because
❼ They are immutable.
❼ They have no attributes.
❼ You don’t have to use new to create one.
In this chapter, we use two objects from Java libraries, Point and Rectangle.
But first, I want to make it clear that these points and rectangles are not
graphical objects that appear on the screen. They are values that contain
data, just like ints and doubles. Like other values, they are used internally
to perform computations.
9.2
Packages
The Java libraries are divided into packages, including java.lang, which
contains most of the classes we have used so far, and java.awt, the Ab-
stract Window Toolkit (AWT), which contains classes for windows, but-
tons, graphics, etc.
108
Chapter 9. Mutable objects
To use a class defined in another package, you have to import it. Point and
Rectangle are in the java.awt package, so to import them like this:
import java.awt.Point;
import java.awt.Rectangle;
All import statements appear at the beginning of the program, outside the
class definition.
The classes in java.lang, like Math and String, are imported automatically,
which is why we haven’t needed the import statement yet.
9.3
Point objects
A point is two numbers (coordinates) that we treat collectively as a single
object. In mathematical notation, points are often written in parentheses,
with a comma separating the coordinates. For example, (0, 0) indicates the
origin, and (x, y) indicates the point x units to the right and y units up from
the origin.
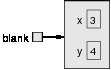
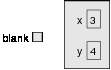
In Java, a point is represented by a Point object. To create a new point,
you have to use new:
Point blank;
blank = new Point(3, 4);
The first line is a conventional variable declaration: blank has type Point.
The second line invokes new, specifies the type of the new object, and provides
arguments. The arguments are the coordinates of the new point, (3, 4).
The result of new is a reference to the new point, so blank contains a
reference to the newly-created object. There is a standard way to diagram
this assignment, shown in the figure.
As usual, the name of the variable blank appears outside the box and its
value appears inside the box. In this case, that value is a reference, which
9.4. Instance variables
109
is shown graphically with an arrow. The arrow points to the object we’re
referring to.
The big box shows the newly-created object with the two values in it. The
names x and y are the names of the instance variables.
Taken together, all the variables, values, and objects in a program are called
the state. Diagrams like this that show the state of the program are called
state diagrams. As the program runs, the state changes, so you should
think of a state diagram as a snapshot of a particular point in the execution.
9.4
Instance variables
The pieces of data that make up an object are called instance variables
because each object, which is an instance of its type, has its own copy of
the instance variables.
It’s like the glove compartment of a car. Each car is an instance of the type
“car,” and each car has its own glove compartment. If you ask me to get
something from the glove compartment of your car, you have to tell me which
car is yours.
Similarly, if you want to read a value from an instance variable, you have to
specify the object you want to get it from. In Java this is done using “dot
notation.”
int x = blank.x;
The expression blank.x means “go to the object blank refers to, and get
the value of x.” In this case we assign that value to a local variable named
x. There is no conflict between the local variable named x and the instance
variable named x. The purpose of dot notation is to identify which variable
you are referring to unambiguously.
You can use dot notation as part of any Java expression, so the following are
legal.
System.out.println(blank.x + ", " + blank.y);
int distance = blank.x * blank.x + blank.y * blank.y;
The first line prints 3, 4; the second line calculates the value 25.
110
Chapter 9. Mutable objects
9.5
Objects as parameters
You can pass objects as parameters in the usual way. For example:
public static void printPoint(Point p) {
System.out.println("(" + p.x + ", " + p.y + ")");
}
This method takes a point as an argument and prints it in the stan-
dard format.
If you invoke printPoint(blank), it prints (3, 4).
Ac-
tually, Java already has a method for printing Points.
If you invoke
System.out.println(blank), you get
java.awt.Point[x=3,y=4]
This is a standard format Java uses for printing objects. It prints the name
of the type, followed by the names and values of the instance variables.
As a second example, we can rewrite the distance method from Section 6.2
so that it takes two Points as parameters instead of four doubles.
public static double distance(Point p1, Point p2) {
double dx = (double)(p2.x - p1.x);
double dy = (double)(p2.y - p1.y);
return Math.sqrt(dx*dx + dy*dy);
}
The typecasts are not really necessary; I added them as a reminder that the
instance variables in a Point are integers.
9.6
Rectangles
Rectangles are similar to points, except that they have four instance vari-
ables: x, y, width and height. Other than that, everything is pretty much
the same.
This example creates a Rectangle object and makes box refer to it.
Rectangle box = new Rectangle(0, 0, 100, 200);
This figure shows the effect of this assignment.

9.7. Objects as return types
111
If you print box, you get
java.awt.Rectangle[x=0,y=0,width=100,height=200]
Again, this is the result of a Java method that knows how to print Rectangle
objects.
9.7
Objects as return types
You can write methods that return objects. For example, findCenter takes a
Rectangle as an argument and returns a Point that contains the coordinates
of the center of the Rectangle:
public static Point findCenter(Rectangle box) {
int x = box.x + box.width/2;
int y = box.y + box.height/2;
return new Point(x, y);
}
Notice that you can use new to create a new object, and then immediately
use the result as a return value.
9.8
Objects are mutable
You can change the contents of an object by making an assignment to one of
its instance variables. For example, to “move” a rectangle without changing
its size, you can modify the x and y values:
box.x = box.x + 50;
box.y = box.y + 100;
The result is shown in the figure:

112
Chapter 9. Mutable objects
We can encapsulate this code in a method and generalize it to move the
rectangle by any amount:
public static void moveRect(Rectangle box, int dx, int dy) {
box.x = box.x + dx;
box.y = box.y + dy;
}
The variables dx and dy indicate how far to move the rectangle in each
direction. Invoking this method has the effect of modifying the Rectangle
that is passed as an argument.
Rectangle box = new Rectangle(0, 0, 100, 200);
moveRect(box, 50, 100);
System.out.println(box);
prints java.awt.Rectangle[x=50,y=100,width=100,height=200].
Modifying objects by passing them as arguments to methods can be useful,
but it can also make debugging more difficult because it is not always clear
which method invocations do or do not modify their arguments. Later, I
discuss some pros and cons of this programming style.
Java provides methods that operate on Points and Rectangles. You can
read the documentation at http://download.oracle.com/javase/6/docs/
api/java/awt/Point.html and http://download.oracle.com/javase/6/
docs/api/java/awt/Rectangle.html.
For example, translate has the same effect as moveRect, but instead of
passing the Rectangle as an argument, you use dot notation:
box.translate(50, 100);
The effect is the same.


9.9. Aliasing
113
9.9
Aliasing
Remember that when you assign an object to a variable, you are assigning a
reference to an object. It is possible to have multiple variables that refer to
the same object. For example, this code:
Rectangle box1 = new Rectangle(0, 0, 100, 200);
Rectangle box2 = box1;
generates a state diagram that looks like this:
box1 and box2 refer to the same object. In other words, this object has two
names, box1 and box2. When a person uses two names, it’s called aliasing.
Same thing with objects.
When two variables are aliased, any changes that affect one variable also
affect the other. For example:
System.out.println(box2.width);
box1.grow(50, 50);
System.out.println(box2.width);
The first line prints 100, which is the width of the Rectangle referred to by
box2. The second line invokes the grow method on box1, which expands the
Rectangle by 50 pixels in every direction (see the documentation for more
details). The effect is shown in the figure:
Whatever changes are made to box1 also apply to box2. Thus, the value
printed by the third line is 200, the width of the expanded rectangle. (As an
aside, it is perfectly legal for the coordinates of a Rectangle to be negative.)

114
Chapter 9. Mutable objects
As you can tell even from this simple example, code that involves aliasing
can get confusing fast, and can be difficult to debug. In general, aliasing
should be avoided or used with care.
9.10
null
When you create an object variable, remember that you are creating a refer-
ence to an object. Until you make the variable point to an object, the value
of the variable is null. null is a special value (and a Java keyword) that
means “no object.”
The declaration Point blank; is equivalent to this initialization
Point blank = null;
and is shown in the following state diagram:
The value null is represented by a small square with no arrow.
If you try to use a null object, either by accessing an instance variable or
invoking a method, Java throws a NullPointerException, prints an error
message and terminates the program.
Point blank = null;
int x = blank.x;
// NullPointerException
blank.translate(50, 50);
// NullPointerException
On the other hand, it is legal to pass a null object as an argument or receive
one as a return value. In fact, it is common to do so, for example to represent
an empty set or indicate an error condition.
9.11
Garbage collection
In Section 9.9 we talked about what happens when more than one variable
refers to the same object. What happens when no variable refers to an
object? For example:
Point blank = new Point(3, 4);
blank = null;
9.12. Objects and primitives
115
The first line creates a new Point object and makes blank refer to it. The
second line changes blank so that instead of referring to the object, it refers
to nothing (the null object).
If no one refers to an object, then no one can read or write any of its values,
or invoke a method on it. In effect, it ceases to exist. We could keep the
object in memory, but it would only waste space, so periodically as your
program runs, the system looks for stranded objects and reclaims them, in
a process called garbage collection. Later, the memory space occupied by
the object will be available to be used as part of a new object.
You don’t have to do anything to make garbage collection work, and in
general you will not be aware of it. But I thought you should know.
9.12
Objects and primitives
There are two kinds of types in Java, primitive types and object types. Prim-
itives, like int and boolean begin with lower-case letters; object types begin
with upper-case letters. This distinction is useful because it reminds us of
some of the differences between them:
❼ When you declare a primitive variable, you get storage space for a
primitive value. When you declare an object variable, you get a space
for a reference to an object. to get space for the object itself, you have
to use new.
❼ If you don’t initialize a primitive type, it is given a default value that
depends on the type. For example, 0 for ints and true for booleans.
The default value for object types is null, which indicates no object.
❼ Primitive variables are well isolated in the sense that there is nothing
you can do in one method that will affect a variable in another method.
116
Chapter 9. Mutable objects
Object variables can be tricky to work with because they are not as
well isolated. If you pass a reference to an object as an argument, the
method you invoke might modify the object, in which case you will see
the effect. Of course, that can be a good thing, but you have to be
aware of it.
There is one other difference between primitives and object types. You can-
not add new primitives to Java (unless you get yourself on the standards
committee), but you can create new object types! We’ll see how in the next
chapter.
9.13
Glossary
package: A collection of classes. Java classes are organized in packages.
AWT: The Abstract Window Toolkit, one of the biggest and most
commonly-used Java packages.
instance: An example from a category. My cat is an instance of the category
“feline things.” Every object is an instance of some class.
instance variable: One of the named data items that make up an object.
Each object (instance) has its own copy of the instance variables for its
class.
reference: A value that indicates an object. In a state diagram, a reference
appears as an arrow.
aliasing: The condition when two or more variables refer to the same object.
garbage collection: The process of finding objects that have no references
and reclaiming their storage space.
state: A complete description of all the variables and objects and their val-
ues, at a given point during the execution of a program.
state diagram: A snapshot of the state of a program, shown graphically.
9.14. Exercises
117
9.14
Exercises
Exercise 9.1.
1. For the following program, draw a stack diagram show-
ing the local variables and parameters of main and riddle, and show
any objects those variables refer to.
2. What is the output of this program?
public static void main(String[] args)
{
int x = 5;
Point blank = new Point(1, 2);
System.out.println(riddle(x, blank));
System.out.println(x);
System.out.println(blank.x);
System.out.println(blank.y);
}
public static int riddle(int x, Point p)
{
x = x + 7;
return x + p.x + p.y;
}
The point of this exercise is to make sure you understand the mechanism for
passing Objects as parameters.
Exercise 9.2.
1. For the following program, draw a stack diagram show-
ing the state of the program just before distance returns. Include all
variables and parameters and the objects those variables refer to.
2. What is the output of this program?
public static double distance(Point p1, Point p2) {
int dx = p1.x - p2.x;
int dy = p1.y - p2.y;
return Math.sqrt(dx*dx + dy*dy);
}
public static Point findCenter(Rectangle box) {
118
Chapter 9. Mutable objects
int x = box.x + box.width/2;
int y = box.y + box.height/2;
return new Point(x, y);
}
public static void main(String[] args) {
Point blank = new Point(5, 8);
Rectangle rect = new Rectangle(0, 2, 4, 4);
Point center = findCenter(rect);
double dist = distance(center, blank);
System.out.println(dist);
}
Exercise 9.3. The method grow is part of the Rectangle class.
Read
the documentation at http: // download. oracle. com/ javase/ 6/ docs/
api/ java/ awt/ Rectangle. html# grow( int,int) .
1. What is the output of the following program?
2. Draw a state diagram that shows the state of the program just before
the end of main. Include all local variables and the objects they refer
to.
3. At the end of main, are p1 and p2 aliased? Why or why not?
public static void printPoint(Point p) {
System.out.println("(" + p.x + ", " + p.y + ")");
}
public static Point findCenter(Rectangle box) {
int x = box.x + box.width/2;
int y = box.y + box.height/2;
return new Point(x, y);
}
public static void main(String[] args) {
9.14. Exercises
119
Rectangle box1 = new Rectangle(2, 4, 7, 9);
Point p1 = findCenter(box1);
printPoint(p1);
box1.grow(1, 1);
Point p2 = findCenter(box1);
printPoint(p2);
}
Exercise 9.4. You might be sick of the factorial method by now, but we’re
going to do one more version.
1. Create a new program called Big.java and write an iterative version
of factorial.
2. Print a table of the integers from 0 to 30 along with their factorials. At
some point around 15, you will probably see that the answers are not
right any more. Why not?
3. BigIntegers are Java objects that can represent arbitrarily big in-
tegers.
There is no upper bound except the limitations of mem-
ory size and processing speed.
Read the documentation of Big-
Integers at http: // download. oracle. com/ javase/ 6/ docs/ api/
java/ math/ BigInteger. html .
4. To use BigIntegers, you have to add import java.math.BigInteger
to the beginning of your program.
5. There are several ways to create a BigInteger, but the one I recommend
uses valueOf. The following code converts an integer to a BigInteger:
int x = 17;
BigInteger big = BigInteger.valueOf(x);
Type in this code and try it out. Try printing a BigInteger.
6. Because BigIntegers are not primitive types, the usual math operators
don’t work. Instead we have to use methods like add. To add two
BigIntegers, invoke add on one and pass the other as an argument.
For example:
120
Chapter 9. Mutable objects
BigInteger small = BigInteger.valueOf(17);
BigInteger big = BigInteger.valueOf(1700000000);
BigInteger total = small.add(big);
Try out some of the other methods, like multiply and pow.
7. Convert factorial so that it performs its calculation using BigIntegers
and returns a BigInteger as a result.
You can leave the parameter
alone—it will still be an integer.
8. Try printing the table again with your modified factorial method. Is
it correct up to 30? How high can you make it go? I calculated the
factorial of all the numbers from 0 to 999, but my machine is pretty
slow, so it took a while. The last number, 999!, has 2565 digits.
Exercise 9.5. Many encryption techniques depend on the ability to raise
large integers to an integer power. Here is a method that implements a (rea-
sonably) fast technique for integer exponentiation:
public static int pow(int x, int n) {
if (n==0) return 1;
// find x to the n/2 recursively
int t = pow(x, n/2);
// if n is even, the result is t squared
// if n is odd, the result is t squared times x
if (n%2 == 0) {
return t*t;
} else {
return t*t*x;
}
}
The problem with this method is that it only works if the result is smaller
than 2 billion. Rewrite it so that the result is a BigInteger. The parameters
should still be integers, though.
You can use the BigInteger methods add and multiply, but don’t use pow,
which would spoil the fun.
9.14. Exercises
121
Exercise 9.6. If you are interested in graphics, now is a good time to read
Appendix A and do the exercises there.
122
Chapter 9. Mutable objects










