Aiming radio antennas to target a particular area of the world requires calculation of the great circle bearing between your location and the other stations’ location. That bearing is calculated from some simple spherical trigonometry using a hand-held calculator or a computer program. Before talking about the maths, however, we need to establish a frame of reference that makes the system work.
The need for navigation on the surface of the Earth caused the creation of a grid system uniquely to locate points on the surface of our globe. Longitude lines run from the north pole to the south pole, i.e. from north to south.
The reference point (longitude zero), called the prime meridian, runs through Greenwich, England. The longitude of the prime meridian is 0 degrees. Longitudes west of the prime meridian are given a plus sign (+), while longitudes east of the prime are given a minus (−) sign. If you continue the prime meridian through the poles to the other side of the Earth it has a longitude of 180 degrees. Thus, the longitude values run from −180 degrees to +180 degrees, with ±180 degrees being the same line.
The observatory at Greenwich is also the point against which relative time is measured. Every 15 degree change of longitude is equivalent to a one hour difference with the Greenwich time. To the west, subtract one hour for each 15 degrees and to the east add one
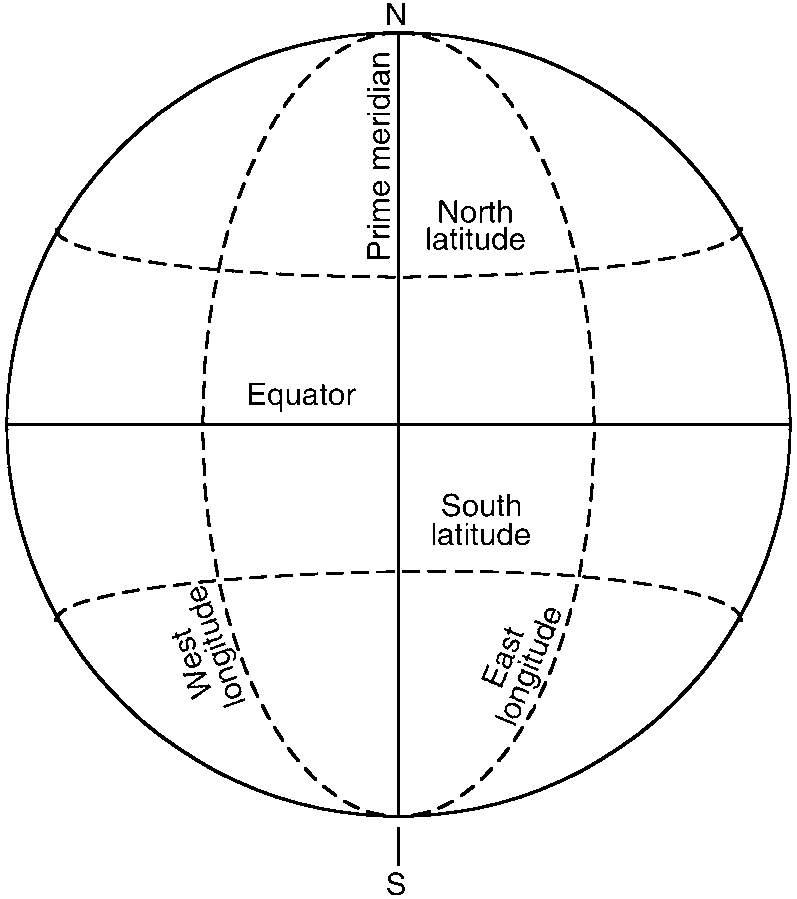Figure 24.1 Lines of longitude and latitude
hour for each 15 degrees. Thus, the time on the East Coast of the United States is −5 hours relative to Greenwich time. At one time, we called time along the prime meridian Greenwich mean time (GMT), also called Zulu time to simplify matters for CW operators.
Latitude lines are measured against the equator, with distances north of the equator being taken as positive, and distances south of the equator being negative. The equator is 0 degrees latitude, while the north pole is +90 degrees latitude and the south pole is −90 degrees latitude.
Long ago navigators learned that the latitude can be measured by ‘shooting’ the stars and consulting a special atlas to compare the angle of certain stars with tables that translate to latitude numbers. The longitude measurement, however, is a bit different. For centuries sailors could measure latitude, but had to guess longitude (often with tragic results). In the early eighteenth century, the British government offered a large cash prize to anyone who could design a chronometer that could be taken to sea. By keeping the chronometer set accurately to Greenwich mean time, and comparing GMT against local time (i.e. at a time like high noon when the position of the sun is easy to judge), the longitude could be calculated. If you are interested in this subject, then most decent libraries have books on celestial navigation.
Consider two points on a globe: ‘A’ is your location, while ‘B’ is the other station’s location. The distance ‘D’ is the great circle path between ‘A’ and ‘B’.
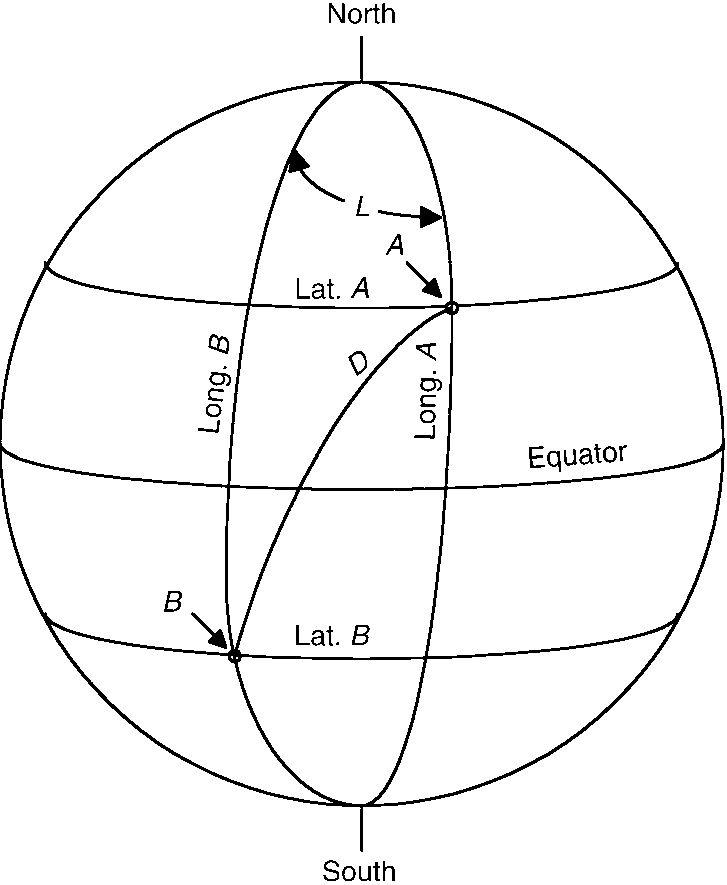Figure 24.2 Great circle path
The great circle path length can be expressed in either degrees or distance (e.g. miles, nautical miles or kilometres). To calculate the distance, it is necessary to find the difference in longitude (L) between your longitude (LA) and the other station’s longitude (LB): L = LA−LB. Keep the signs straight. For example, if your longitude (LA) is 40 degrees, and the other station’s longitude (LB)is −120 degrees, then L = 40−(−120) = 40+ 120 = 160. The equation for distance (D)is:
cosD = (sinA× sinB)+(cosA× cosB × cosL)where:
D is the angular great circle distance
A is your latitude
B is the other station’s latitude.
To find the actual angle, take the arccos of the above equation, i.e.
In the next equation you will want to use D in angular measure, but later on will want to convert D to miles. To do this, multiply D in degrees by 69.4. Or, if you prefer metric measures, then D × 111.2 yields kilometres. This is the approximate distance in statute miles between ‘A’ and ‘B’.
To find the bearing from true north, work the equation below:C
=
arccos
sinB −(sinA× cosD) (cosA× sinD) However, this equation won’t always give you the right answer unless you make some corrections.
The first problem is the ‘same longitude error’, i.e. when both stations are on the same longitude line. In this case, L = LA−LB = 0. If LATA> LAT B,then C = 180 degrees, but if LATA< LAT B, then C = 0 degrees. If LAT A = LAT B, then what’s the point of all these calculations?
The next problem is found when the condition −180æ ≤ L≤+180æ is not met, i.e. when the absolute value of L is greater than 180æ, ABS(L) > 180æ. In this case, either add or subtract 360 in order to make the value between ±180æ:
IfL> +180,then L = L− 360 IfL< −180,then L = L+ 360One problem seen while calculating these values on a computer or hand calculator is the fact that the sin(X)and cos(X) cover different ranges. The sin(X) function returns values from 0æ to 360æ, while the cos(X) function returns values only over 0æ to 180æ.If L is positive, then the result bearing C is accurate, but if L is negative then the actual value of C = 360−C. The following test is necessary:
If L<0then L = 360−L Else L = L End if
Another problem is seen whenever either station is in a high latitude near either pole (±90æ), or where both locations are very close together, or where the two locations are antipodal (i.e. on opposite points on the Earth’s surface). The best way to handle these problems is to use a different equation that multiplies by the cosecant of D (i.e. cosec(D)), rather than dividing by sine of D (i.e. sin(D)).