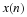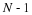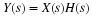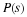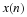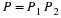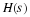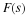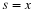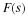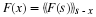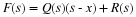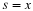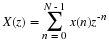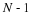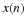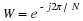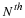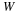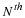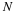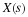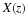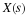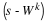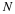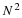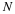One of the main applications of the FFT is to do convolution more efficiently than the direct calculation from the definition which is:
which, with a change of variables, can also be written as:
This is often used to filter a signal x(n) with a filter whose impulse response is h(n). Each output value y(n) requires N multiplications and N–1 additions if y(n) and h(n) have N terms. So, for N output values, on the order of N2 arithmetic operations are required.
Because the DFT converts convolution to multiplication:
can be calculated with the FFT and bring the order of arithmetic operations down to Nlog(N) which can be significant for large N.
This approach, which is called “fast convolutions", is a form of block processing since a whole block or segment of x(n) must be available to calculate even one output value, y(n). So, a time delay of one block length is always required. Another problem is the filtering use of convolution is usually non-cyclic and the convolution implemented with the DFT is cyclic. This is dealt with by appending zeros to x(n) and h(n) such that the output of the cyclic convolution gives one block of the output of the desired non-cyclic convolution.
For filtering and some other applications, one wants “on going" convolution where the filter response h(n) may be finite in length or duration, but the input x(n) is of arbitrary length. Two methods have traditionally used to break the input into blocks and use the FFT to convolve the block so that the output that would have been calculated by directly implementing Equation 13.1 or Equation 13.2 can be constructed efficiently. These are called “overlap-add" and “over-lap save".
In order to use the FFT to convolve (or filter) a long input sequence x(n) with a finite length-M impulse response, h(n), we partition the input sequence in segments or blocks of length L. Because convolution (or filtering) is linear, the output is a linear sum of the result of convolving the first block with h(n) plus the result of convolving the second block with h(n), plus the rest. Each of these block convolutions can be calculated by using the FFT. The output is the inverse FFT of the product of the FFT of x(n) and the FFT of h(n). Since the number of arithmetic operation to calculate the convolution directly is on the order of M2 and, if done with the FFT, is on the order of Mlog(M), there can be a great savings by using the FFT for large M.
The reason this procedure is not totally straightforward, is the length of the output of convolving a length-L block with a length-M filter is of length L+M–1. This means the output blocks cannot simply be concatenated but must be overlapped and added, hence the name for this algorithm is “Overlap-Add".
The second issue that must be taken into account is the fact that the overlap-add steps need non-cyclic convolution and convolution by the FFT is cyclic. This is easily handled by appending L–1 zeros to the impulse response and M–1 zeros to each input block so that all FFTs are of length M+L–1. This means there is no aliasing and the implemented cyclic convolution gives the same output as the desired non-cyclic convolution.
The savings in arithmetic can be considerable when implementing convolution or performing FIR digital filtering. However, there are two penalties. The use of blocks introduces a delay of one block length. None of the first block of output can be calculated until all of the first block of input is available. This is not a problem for “off line" or “batch" processing but can be serious for real-time processing. The second penalty is the memory required to store and process the blocks. The continuing reduction of memory cost often removes this problem.
The efficiency in terms of number of arithmetic operations per output point increases for large blocks because of the Mlog(M) requirements of the FFT. However, the blocks become very large (L>>M), much of the input block will be the appended zeros and efficiency is lost. For any particular application, taking the particular filter and FFT algorithm being used and the particular hardware being used, a plot of efficiency vs. block length, L should be made and L chosen to maximize efficiency given any other constraints that are applicable.
Usually, the block convolutions are done by the FFT, but they could be done by any efficient, finite length method. One could use “rectangular transforms" or “number-theoretic transforms". A generalization of this method is presented later in the notes.
An alternative approach to the Overlap-Add can be developed by starting with segmenting the output rather than the input. If one considers the calculation of a block of output, it is seen that not only the corresponding input block is needed, but part of the preceding input block also needed. Indeed, one can show that a length M+L–1 segment of the input is needed for each output block. So, one saves the last part of the preceding block and concatenates it with the current input block, then convolves that with h(n) to calculate the current output
Convolution is intimately related to the DFT. It was shown in The DFT as Convolution or Filtering that a prime length DFT could be converted to cyclic convolution. It has been long known 48 that convolution can be calculated by multiplying the DFTs of signals.
An important question is what is the fastest method for calculating digital convolution. There are several methods that each have some advantage. The earliest method for fast convolution was the use of sectioning with overlap-add or overlap-save and the FFT 48, 53, 10. In most cases the convolution is of real data and, therefore, real-data FFTs should be used. That approach is still probably the fastest method for longer convolution on a general purpose computer or microprocessor. The shorter convolutions should simply be calculated directly.
The partitioning of long or infinite strings of data into shorter sections or blocks has been used to allow application of the FFT to realize on-going or continuous convolution 57, 30. This section develops the idea of block processing and shows that it is a generalization of the overlap-add and overlap-save methods 57, 26. They further generalize the idea to a multidimensional formulation of convolution 3, 15. Moving in the opposite direction, it is shown that, rather than partitioning a string of scalars into blocks and then into blocks of blocks, one can partition a scalar number into blocks of bits and then include the operation of multiplication in the signal processing formulation. This is called distributed arithmetic 14 and, since it describes operations at the bit level, is completely general. These notes try to present a coherent development of these ideas.
In this section the usual convolution and recursion that implements FIR
and IIR discrete-time filters are reformulated in terms of vectors and
matrices. Because the same data is partitioned and grouped in a variety
of ways, it is important to have a consistent notation in order to be
clear. The nth element of a data sequence is expressed h(n) or, in
some cases to simplify, hn. A block or finite length column vector is
denoted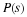 
with n indicating the nth block or
section of a longer vector. A matrix, square or rectangular, is indicated
by an upper case letter such as H with a subscript if appropriate.
The operation of a finite impulse response (FIR) filter is described by a finite convolution as
where x(n) is causal, h(n) is causal and of length L, and the time index n goes from zero to infinity or some large value. With a change of index variables this becomes
which can be expressed as a matrix operation by
The H matrix of impulse response values is partitioned into N by N square sub matrices and the X and Y vectors are partitioned into length-N blocks or sections. This is illustrated for N=3 by
Substituting these definitions into Equation 13.6 gives
The general expression for the nth output block is
which is a vector or block convolution. Since the matrix-vector multiplication within the block convolution is itself a convolution, Equation 13.10 is a sort of convolution of convolutions and the finite length matrix-vector multiplication can be carried out using the FFT or other fast convolution methods.
The equation for one output block can be written as the product
and the effects of one input block can be written
These are generalize statements of overlap save and overlap add 57, 26. The block length can be longer, shorter, or equal to the filter length.
Although less well-known, IIR filters can also be implemented with block processing 24, 18, 59, 12, 13. The block form of an IIR filter is developed in much the same way as for the block convolution implementation of the FIR filter. The general constant coefficient difference equation which describes an IIR filter with recursive coefficients al, convolution coefficients bk, input signal x(n), and output signal y(n) is given by
using both functional notation and subscripts, depending on which is easier and clearer. The impulse response h(n) is
which can be written in matrix operator form
In terms of N by N submatrices and length-N blocks, this becomes
From this formulation, a block recursive equation can be written that will generate the impulse response block by block.
with initial conditions given by
This can also be written to generate the square partitions of the impulse response matrix by
with initial conditions given by
ane K=–A0–1A1. This recursively generates square submatrices of H similar to those defined in Equation 13.7 and Equation 13.9 and shows the basic structure of the dynamic system.
Next, we develop the recursive formulation for a general input as described by the scalar difference equation Equation 13.14 and in matrix operator form by
which, after substituting the definitions of the sub matrices and assuming the block length is larger than the order of the numerator or denominator, becomes
From the partitioned rows of Equation 13.24, one can write the block recursive relation
Solving for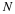 
gives
which is a first order vector difference equation 12, 13. This is the fundamental block recursive algorithm that implements the original scalar difference equation in Equation 13.14. It has several important characteristics.
The block recursive formulation is similar to a state variable equation but the states are blocks or sections of the output 13, 34, 63, 64.
The eigenvalues of K are the poles of the original scalar problem raised to the N power plus others that are zero. The longer the block length, the “more stable" the filter is, i.e. the further the poles are from the unit circle 12, 13, 63, 8, 11.
If the block length were shorter than the denominator, the vector difference equation would be higher than first order. There would be a non zero A2. If the block length were shorter than the numerator, there would be a non zero B2 and a higher order block convolution operation. If the block length were one, the order of the vector equation would be the same as the scalar equation. They would be the same equation.
The actual arithmetic that goes into the calculation of the output is partly recursive and partly convolution. The longer the block, the more the output is calculated by convolution and, the more arithmetic is required.
It is possible to remove the zero eigenvalues in K by making K rectangular or square and N by N This results in a form even more similar to a state variable formulation 42,