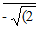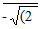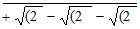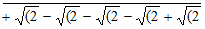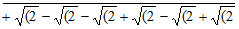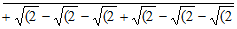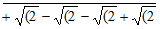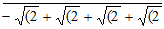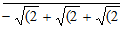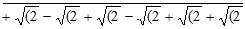In the above sub –chapter we observed exact value of integer angles. In this sub –chapter, we shall discuss the exact length of few of the polygons using Precise –Rewritten method. Guru Euclid is father of polygonal geometry. No one Himafter developed such huge contribution on polygon yet. This sub –chapter is in His respect.
For any regular polygon, there is pattern for chord or length of a side. If quotient on dividing 360 by the given angle is an integer, that is regular polygon for this purpose. For example
360°/1 °= 360 (this is 360 –gon, 1° has exact value in pattern)
360°/18.94737°= 19 (this is 19 –gon, 18.94737° has exact value in pattern)
=360°/0.125874125874126°= 2860 (this is 2860 –gon, 0.125874125874126° has exact value in pattern)
As a result, angle which is 360°/n [where n is a natural] has exact value of trigonometry. Following is the length of a side of regular polygon up to n= 24.
[Closing brackets have collapsed for easy.]
N –gon Each side exact length
3 √(2 + √(2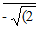 
]
4 √2
5 √(2 – √(2 
]
6 √(2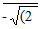 
]
7 √(2 –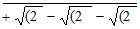 
]
8 √(2 – √2]
9 √(2 – √(2 + √(2 – √(2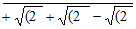 
]
10 √(2 ]
11 √(2 – √(2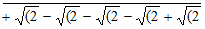 
]
12 √(2 – √(2 + √(2 ]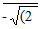
13 √(2 – √(2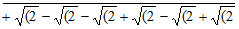 
]
14 √(2 – √(2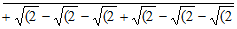 
]
15 √(2 – √(2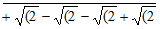 
]
16 √(2 – √(2 + √(2]
17 √(2 – √(2 + √(2 + √(2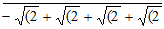 
]
18 √(2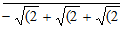 
]
19 √(2 – √(2 + √(2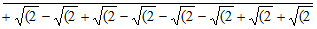 
]
20 √(2 – √(2 + √(2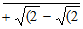 
]
21 √(2 – √(2 + √(2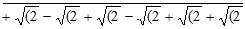 
]
22 √(2 – √(2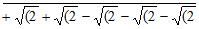 
]
23 √(2 – √(2 
24 √(2 – √(2 + √(2 + √(2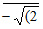 
]
[Closing brackets have collapsed for easy.]