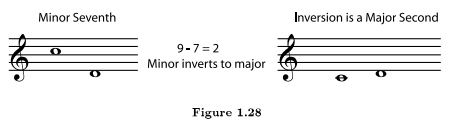Pitch and Interval
Musical notes, like all sounds, are made of sound waves. The sound waves that make musical notes are very evenly-spaced waves, and the qualities of these regular waves - for example how big they are or how far apart they are - affect the sound of the note. A note can be high or low, depending on how often (how frequently) one of its waves arrives at your ear. When scientists and engineers talk about how high or low a sound is, they talk about its frequency2. The higher the frequency of a note, the higher it sounds. They can measure the frequency of notes, and like most measurements, these will be numbers, like "440 vibrations per second."
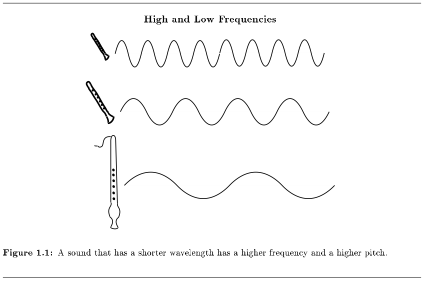
But people have been making music and talking about music since long before we knew that sounds were waves with frequencies. So when musicians talk about how high or low a note sounds, they usually don't talk about frequency; they talk about the note's pitch3. And instead of numbers, they give the notes names, like "C". (For example, musicians call the note with frequency "440 vibrations per second" an "A".) But to see where octaves come from, let's talk about frequencies a little more. Imagine a few men are singing a song together. Nobody is singing harmony; they are all singing the same pitch - the same frequency - for each note.
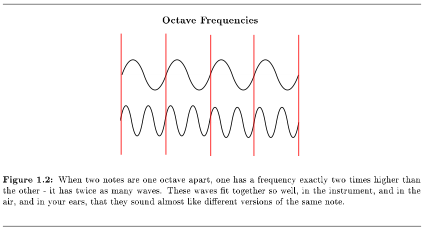
Now some women join in the song. They can't sing where the men are singing; that's too low for their voices. Instead they sing notes that are exactly double the frequency that the men are singing. That means their note has exactly two waves for each one wave that the men's note has. These two frequencies t so well together that it sounds like the women are singing the same notes as the men, in the same key (Section 2.1). They are just singing them one octave higher. Any note that is twice the frequency of another note is one octave higher.
Notes that are one octave apart are so closely related to each other that musicians give them the same name. A note that is an octave higher or lower than a note named "C natural" will also be named "C natural". A note that is one (or more) octaves higher or lower than an "F sharp" will also be an "F sharp". (For more discussion of how notes are related because of their frequencies, see The Harmonic Series4, Standing Waves and Musical Instruments5, and Standing Waves and Wind Instruments6.)
The notes in different octaves are so closely related that when musicians talk about a note, a "G" for example, it often doesn't matter which G they are talking about. We can talk about the "F sharp" in a G major scale (Section 2.1) without mentioning which octave the scale or the F sharp are in, because the scale is the same in every octave. Because of this, many discussions of music theory don't bother naming octaves. Informally, musicians often speak of "the B on the staff" or the "A above the staff", if it's clear which staff7 they're talking about.
But there are also two formal systems for naming the notes in a particular octave. Many musicians use Helmholtz notation. Others prefer scientific pitch notation, which simply labels the octaves with numbers, starting with C1 for the lowest C on a full-sized keyboard. Figure 3 shows the names of the octaves most commonly used in music.
The octave below contra can be labelled CCC or Co; higher octaves can be labelled with higher numbers or more lines. Octaves are named from one C to the next higher C. For example, all the notes between "great C" and "small C" are "great". One-line c is also often called "middle C". No other notes are called "middle", only the C.
Example 1.1
Exercise 1.1.1
(Solution on p. 25.)
Give the correct octave name for each note.
The word "octave" comes from a Latin root meaning "eight". It seems an odd name for a frequency that is two times, not eight times, higher. The octave was named by musicians who were more interested in how octaves are divided into scales, than in how their frequencies are related. Octaves aren't the only notes that sound good together. The people in different musical traditions have different ideas about what notes they think sound best together. In the Western8 musical tradition - which includes most familiar music from Europe and the Americas - the octave is divided up into twelve equally spaced notes. If you play all twelve of these notes within one octave you are playing a chromatic scale (p. 7). Other musical traditions - traditional Chinese music for example - have divided the octave differently and so they use different scales. (Please see Major Keys and Scales (Section 2.1), Minor Keys and Scales (Section 2.2), and Scales that aren't Major or Minor9 for more about this.)
You may be thinking "OK, that's twelve notes; that still has nothing to do with the number eight", but out of those twelve notes, only seven are used in any particular major (Section 2.1) or minor (Section 2.2) scale. Add the first note of the next octave, so that you have that a "complete"-sounding scale ("do-remi-fa-so-la-ti" and then "do" again), and you have the eight notes of the octave. These are the diatonic scales, and they are the basis of most Western10 music.
Now take a look at the piano keyboard. Only seven letter names are used to name notes: A, B, C, D, E, F, and G. The eighth note would, of course, be the next A, beginning the next octave. To name the other notes, the notes on the black piano keys, you have to use a sharp or flat11 sign.
Whether it is a popular song, a classical symphony, or an old folk tune, most of the music that feels comfortable and familiar (to Western listeners) is based on either a major or minor scale. It is tonal music that mostly uses only seven of the notes within an octave: only one of the possible A's (A sharp, A natural, or A at), one of the possible B's (B sharp, B natural, or B at), and so on. The other notes in the chromatic scale are (usually) used sparingly to add interest or to (temporarily) change the key in the middle of the music. For more on the keys and scales that are the basis of tonal music, see Major Keys and Scales (Section 2.1) and Minor Keys and Scales (Section 2.2).
The pitch of a note is how high or low it sounds. Musicians often find it useful to talk about how much higher or lower one note is than another. This distance between two pitches is called the interval between them. In Western music13, the small interval from one note to the next closest note higher or lower is called a half step or semitone.
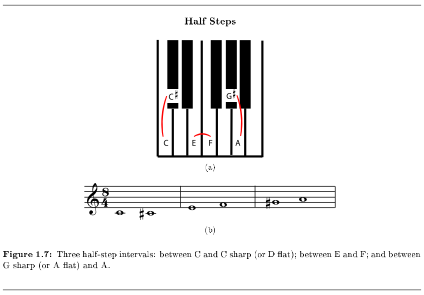
Listen14 to the half steps in Figure 1.7 (Half Steps).
The intervals in Figure 1.7 (Half Steps) look different on a staff15; sometimes they are on the same line, sometimes not. But it is clear at the keyboard that in each case there is no note in between them.
So a scale (Section 2.1) that goes up or down by half steps, a chromatic scale, plays all the notes on both the white and black keys of a piano. It also plays all the notes easily available on most Western16 instruments. (A few instruments, like trombone17 and violin18, can easily play pitches that aren't in the chromatic scale, but even they usually don't.)
Listen19 to a chromatic scale.
If you go up or down two half steps from one note to another, then those notes are a whole step, or whole tone apart.
A whole tone scale, a scale made only of whole steps, sounds very different from a chromatic scale.
Listen20 to a whole tone scale.
You can count any number of whole steps or half steps between notes; just remember to count all sharp or at notes (the black keys on a keyboard) as well as all the natural notes (the white keys) that are in between.
Example 1.2
The interval between C and the F above it is 5 half steps, or two and a half steps.
Exercise 1.2.1
(Solution on p. 25.)
Identify the intervals below in terms of half steps and whole steps. If you have trouble keeping track of the notes, use a piano keyboard, a written chromatic scale, or the chromatic fingerings for your instrument to count half steps.
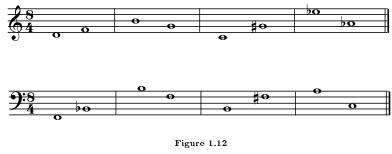
Exercise 1.2.2
(Solution on p. 25.)
Fill in the second note of the interval indicated in each measure. If you need staff paper for this exercise, you can print out this staff paper21 PDF file.
The interval between two notes is the distance between the two pitches23 - in other words, how much higher or lower one note is than the other. This concept is so important that it is almost impossible to talk about scales (Section 2.1), chords24, harmonic progression25, cadence (Section 3.4), or dissonance (Section 3.5) without referring to intervals. So if you want to learn music theory, it would be a good idea to spend some time getting comfortable with the concepts below and practicing identifying intervals.
Scientists usually describe the distance between two pitches in terms of the difference between their frequencies26. Musicians find it more useful to talk about interval. Intervals can be described using half steps and whole steps (Section 1.2). For example, you can say "B natural is a half step below C natural", or "E at is a step and a half above C natural". But when we talk about larger intervals in the major/minor system (Section 1.1), there is a more convenient and descriptive way to name them.
The first step in naming the interval is to find the distance between the notes as they are written on the staff. Count every line and every space in between the notes, as well as the lines or spaces that the notes are on. This gives you the number for the interval.
Example 1.3
To find the interval, count the lines or spaces that the two notes are on as well as all the lines or spaces in between. The interval between B and D is a third. The interval between A and F is a sixth. Note that, at this stage, key signature27, clef28, and accidentals29 do not matter at all.
The simple intervals are one octave or smaller.
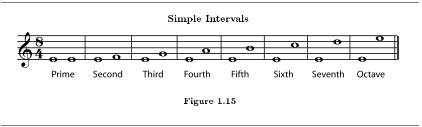
If you like you can listen to each interval as written in Figure 1.15 (Simple Intervals): prime30, second31, third32, fourth33, fth34, sixth35, seventh36, octave37.
Compound intervals are larger than an octave.
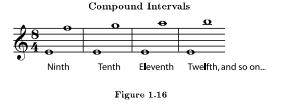
Listen to the compound intervals in Figure 1.16 (Compound Intervals): ninth38, tenth39, eleventh40.
(Solution on p. 26.)
Exercise 1.3.1
Name the intervals.
Exercise 1.3.2
(Solution on p. 26.)
Write a note that will give the named interval.
So far, the actual distance, in half-steps, between the two notes has not mattered. But a third made up of three half-steps sounds different from a third made up of four half-steps. And a fifth made up of seven half steps sounds very different from one of only six half-steps. So in the second step of identifying an interval, clef41, key signature42, and accidentals43 become important.
Listen to the differences in the thirds44 and the fifths45 in Figure 1.19.
So the second step to naming an interval is to classify it based on the number of half steps (Section 1.2) in the interval. Familiarity with the chromatic scale (p. 7) is necessary to do this accurately.
1.3.3.1 Perfect Intervals
Primes, octaves, fourths, and fifths can be perfect intervals.
NOTE: These intervals are never classified as major or minor, although they can be augmented or diminished (see below (Section 1.3.3.3: Augmented and Diminished Intervals)).
What makes these particular intervals perfect? The physics of sound waves (acoustics) shows us that the notes of a perfect interval are very closely related to each other. (For more information on this, see Frequency, Wavelength, and Pitch46 and Harmonic Series47.) Because they are so closely related, they sound particularly good together, a fact that has been noticed since at least the times of classical Greece, and probably even longer. (Both the octave and the perfect fifth have prominent positions in most of the world's musical traditions.) Because they sound so closely related to each other, they have been given the name "perfect" intervals.
NOTE: Actually, modern equal temperament48 tuning does not give the harmonic-series-based pure49 perfect fourths and fifths. For the music-theory purpose of identifying intervals, this does not matter. To learn more about how tuning affects intervals as they are actually played, see Tuning Systems50.
A perfect prime is also called a unison. It is two notes that are the same pitch51. A perfect octave is the "same" note an octave (Section 1.1) - 12 half-steps - higher or lower. A perfect 5th is 7 half-steps. A perfect fourth is 5 half-steps.
Example 1.4
Listen to the octave52, perfect fourth53, and perfect fifth54.
1.3.3.2 Major and Minor Intervals
Seconds, thirds, sixths, and sevenths can be major intervals or minor intervals. The minor interval is always a half-step smaller than the major interval.
Major and Minor Intervals
Listen to the minor second55, major second56, minor third57, major third58, minor sixth59, major sixth60, minor seventh61, and major seventh62.
Exercise 1.3.3
(Solution on p. 26.)
Give the complete name for each interval.
Exercise 1.3.4
(Solution on p. 27.)
Fill in the second note of the interval given.
1.3.3.3 Augmented and Diminished Intervals
If an interval is a half-step larger than a perfect or a major interval, it is called augmented. An interval that is a half-step smaller than a perfect or a minor interval is called diminished. A double sharp63 or double flat64 is sometimes needed to write an augmented or diminished interval correctly. Always remember, though, that it is the actual distance in half steps between the notes that determines the type of interval, not whether the notes are written as natural, sharp, or double-sharp.
Example 1.6
Listen to the augmented prime65, diminished second66, augmented third67, diminished sixth68, augmented seventh69, diminished octave70, augmented fourth71, and diminished fifth72. Are you surprised that the augmented fourth and diminished fifth sound the same?
Exercise 1.3.5
(Solution on p. 27.)
Write a note that will give the named interval.
As mentioned above, the diminished fifth and augmented fourth sound the same. Both are six half-steps, or three whole tones, so another term for this interval is a tritone. In Western Music73, this unique interval, which cannot be spelled as a major, minor, or perfect interval, is considered unusually dissonant (Section 3.5) and unstable (tending to want to resolve (p. 70) to another interval).
You have probably noticed by now that the tritone is not the only interval that can be "spelled" in more than one way. In fact, because of enharmonic spellings74, the interval for any two pitches can be written in various ways. A major third could be written as a diminished fourth, for example, or a minor second as an augmented prime. Always classify the interval as it is written; the composer had a reason for writing it that way. That reason sometimes has to do with subtle differences in the way different written notes will be interpreted by performers, but it is mostly a matter of placing the notes correctly in the context of the key (Section 2.1), the chord75, and the evolving harmony76. (Please see Beginning Harmonic Analysis (Section 3.3) for more on that subject.)
To invert any interval, simply imagine that one of the notes has moved one octave, so that the higher note has become the lower and vice-versa. Because inverting an interval only involves moving one note by an octave (it is still essentially the "same" note in the tonal system), intervals that are inversions of each other have a very close relationship in the tonal (Section 1.1) system.
To find the inversion of an interval
1. To name the new interval, subtract the name of the old interval from 9.
2. The inversion of a perfect interval is still perfect.
3. The inversion of a major interval is minor, and of a minor interval is major.
4. The inversion of an augmented interval is diminished and of a diminished interval is augmented.
Example 1.7
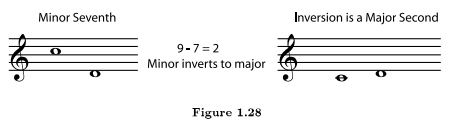
Exercise 1.3.6
(Solution on p. 28.)
What are the inversions of the following intervals?
1. Augmented third
2. Perfect fifth
3. Diminished fifth
4. Major seventh
5. Minor sixth
Here is a quick summary of the above information, for reference.
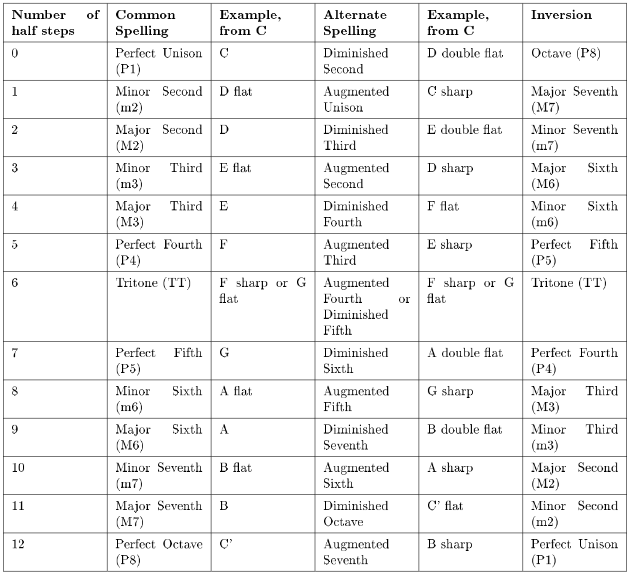
Table 1.1: The examples given name the note reached if one starts on C, and goes up the named interval.
Summary Notes: Perfect Intervals
Summary Notes: Augmented and Diminished Intervals
Summary Notes: Inversions of Intervals
When musicians talk about ear, they don't mean the sense organ itself so much as the brain's ability to perceive, distinguish, and understand what the ear has heard. The term ear training refers to teaching musicians to recognize information about notes79 and chords80 just by hearing them.
A few people have what is called perfect pitch or absolute pitch. These people, when they hear music, can tell you exactly what they are hearing: the G above middle C (p. 4), for example, or the first inversion (Section 3.1.2: First and Second Inversions) of an F minor chord (Section 3.2.1: Major and Minor Chords). A few musicians with particularly perceptive ears can even tell you that a piano is tuned a few cents81 higher than the one that they play at home. This is an unusual skill that even most trained musicians do not have, and research seems to suggest that if you don't have it at a very early age, you cannot develop it. (For more on this subject, you may want to look up Robert Jourdain's Music, the Brain, and Ecstasy: How Music Captures our Imagination.)
However, most musicians can be trained to recognize relative pitch. In other words, if you play two notes, they can tell you that one of them is a major third (Major and Minor Intervals, p. 14) higher than the other. If you play four chords82 in a row, they can tell you that you played a tonic-subdominant-dominant seventh-tonic (I-IV-V7-I) chord progression83.
Fortunately, having relative pitch is good enough, and for many musicians may even be more useful than perfect pitch, because of the way Western84 music is conceived. Since all major keys (Section 2.1) are so similar, a piece in a major key will sound almost exactly the same whether you play it in C major or D major. The thing that matters is not what note you start on, but how all the notes are related to each other and to the "home" note (the tonic (p. 30)) of the key. If someone really wants the piece to be in a different key (because it's easier to sing or play in that key, or just because they want it to sound higher or lower), the whole thing can be transposed85, but the only difference that would make (in the sound) is that the entire piece will sound higher or lower. Most listeners would not even notice the difference, unless you played it in both keys, one right after the other.
NOTE: All minor keys (Section 2.2) are also heard by most listeners as interchangeable, but there are important differences between major keys and minor keys. In fact, the differences in sound between a major key and a minor key is one of the first differences that a musician should be able to hear. If you would like to see whether your "ear" can recognize the difference between major and minor keys, please try the listening exercise (Exercise 2.1.1) in Major Keys and Scales (Exercise 2.1.1).
So, you often don't need to know exactly what notes or chords are being played. Simply having an ear well-trained in "relative pitch" is extremely useful in many ways. Guitar and piano players can figure out chord progressions86 just by listening to them, and then play the progressions in their favorite keys. Other instrumentalists can play a favorite tune without a written copy of it, just by knowing what the interval to the next note must be. Composers and music arrangers can jot down a piece of music without having to "pick it out" on an instrument to find the notes and chords they want. And of course, ear training is crucial to any musician who wants to play jazz or any type of improvisation. Given a well-trained "ear", any musical idea that you "hear" in your head, you can play. And ear training is also crucial for those interested in music theory, musicology, or just being able to write down a tune accurately.
As with all other musical skills, there are many different levels and kinds of proficiency. One musician may be very good at "playing by ear", but may not even read music and cannot name intervals (Section 1.3) or write the music down. Another may be very good at "taking dictation" (writing down the music they hear), and yet feel unable to do jazz improvisation. As always, the key is to practice the particular skills that you want to develop.
1.4.2.1 Tuning
This is the most basic ear training skill, crucial to being able to play music that people will want to hear.
Suggestions
1.4.2.2 Playing Chords By Ear
For instruments that play chordal accompaniments, this is an incredibly useful skill.
Suggestions