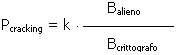Firma Forte Avanzata e Autenticata
firma forte avanzata la cui apposizione viene autenticata da un notaio o da altro pubblico ufficiale autorizzato. L’autenticazione della sottoscrizione consiste nella dichiarazione del pubblico ufficiale che la sottoscrizione è stata apposta in sua presenza. Il documento sottoscritto con questo tipo di firma ha la stessa valenza probatoria della scrittura privata autenticata. L’efficacia probatoria è limitata all’elemento intrinseco della sottoscrizione (la provenienza del documento), senza alcuna interferenza sul contenuto della scrittura (la provenienza della dichiarazione).
2 Al momento il massimo grado di validità legale è quella europea (direttiva 1999/93/CE), che a livello nazionale è stata recepita da tutte le norme emanate dall’anno 2000 in poi.
3 Il termine ‘credenziali di firma’ indica l’insieme delle informazioni di identità e di calcolo necessarie a eseguire il meccanismo di firma digitale (vedi capitolo successivo).
7
Firma Digitale e Non
Crittografia, Riservatezza e Spudoratezza
Crittografia: l'arte della riservatezza
Crittografare un documento significa codificarlo in modo tale che risulti illeggibile a chi non conosce il meccanismo di codifica.
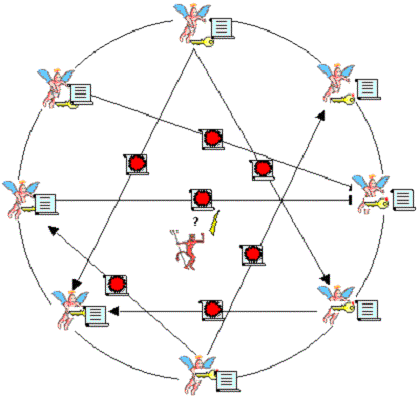
Lo scenario tipico è rappresentato da un gruppo di persone (entità) che vogliono comunicare tra di loro in modo riservato, senza che entità terze (aliene) possano capire il significato dei messaggi scambiati all'interno del gruppo.
Tenuto conto che ogni messaggio è una sequenza di caratteri, e che ogni carattere è rappresentabile in un numero compreso tra 0 e 255 (ovvero un byte), un meccanismo di codifica (crittografia) altro non è che una funzione matematica che permette di convertire la sequenza di caratteri che compone un messaggio (ovvero una sequenza di numeri) in una sequenza di caratteri (numeri) modificati. Il risultato è un nuovo messaggio che risulta incomprensibile a chiunque lo legga.
Ovviamente un meccanismo di semplice codifica non serve a nulla senza un meccanismo complementare di decodifica, ovvero una funzione matematica che permette di convertire il messaggio codificato nel messaggio originale.
Cosa distingue il meccanismo di codifica dal meccanismo di decodifica?
8
Firma Digitale e Non
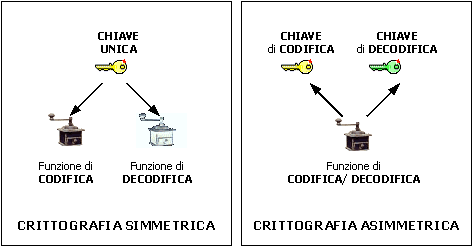
Su questo punto i matematici offrono, al momento, due possibili risposte: 1. l'utilizzo di due funzioni matematiche differenti, ma complementari, associate a un solo parametro numerico, detto chiave di codifica/decodifica;
2. l'utilizzo di una sola funzione matematica associata a due parametri numerici differenti ma complementari, detti rispettivamente chiave di codifica e chiave di decodifica.
In entrambi i casi i matematici ci offrono una soluzione con componenti di due tipi: funzione matematica
parametro numerico (chiave)
in due possibili combinazioni:
due funzioni e una chiave
una funzione e due chiavi.
Poiché il vero problema non sono le funzioni matematiche in gioco, ma le chiavi: 1. nel primo caso si parla di crittografia simmetrica (o a chiavi simmetriche – una sola chiave), 2. nel secondo caso si parla di crittografia asimmetrica (o a chiavi asimmetriche - due chiavi differenti).
Crittografia: le chiavi
Perché il vero problema è rappresentato dalle chiavi e non dalle funzioni?
La risposta è di tipo economico.
Creare nuove chiavi è un processo poco costoso, che può essere ripetuto più e più volte senza particolari problemi. Per contro sviluppare una funzione di crittografia è un processo costoso, e non è ipotizzabile lo sviluppo di una nuova funzione per ogni messaggio che deve essere trasmesso.
Ora nel primo caso (crittografia simmetrica), sia le chiavi che le funzioni utilizzate devono essere conosciute a tutte le entità del gruppo. Purtroppo quando si trasmettono le chiavi a tutte le entità si corre il rischio che entità terze (aliene) intercettino la chiave, vanificando lo sforzo di rendere sicura e riservata la comunicazione.
9
Firma Digitale e Non
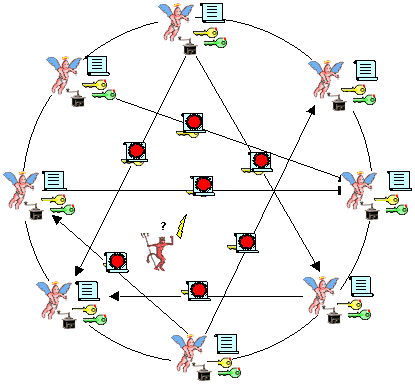
Nel secondo caso (crittografia asimmetrica), questo problema non si pone, in quanto ogni entità del gruppo crea due chiavi: una viene comunicata a tutte le altre entità, e una viene mantenuta rigorosamente segreta. La chiave trasmessa a tutti è di fatto pubblica. In virtù di questo fatto la crittografia asimmetrica viene anche detta crittografia a chiavi pubbliche.
L'uovo di Colombo!
Non proprio.
Quando una entità trasmette a tutte le altre la propria chiave pubblica, deve corredarla di alcune informazioni relative alla propria identità (nominativo). Ora se una entità aliena si maschera da entità del gruppo e trasmette una chiave pubblica falsa dotata di un nominativo vero, le altre entità del gruppo possono essere tratte in inganno, ed essere convinte di parlare con una entità buona invece che con l'aliena.
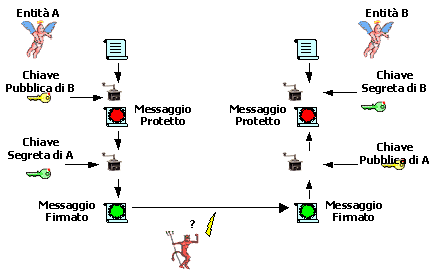
Tuttavia la crittografia asimmetrica ci offre una possibilità in più rispetto alla crittografia simmetrica. Se al momento di trasmettere un messaggio, dopo aver codificato il messaggio con la chiave pubblica del destinatario (in modo tale che solo lui possa decodificarlo con la propria chiave segreta), codifichiamo ulteriormente il messaggio con la nostra chiave segreta, il destinatario non solo ha la ragionevole certezza che nessun altro ha letto il messaggio durante la trasmissione, ma ha anche la ragionevole certezza che ad inviarlo siamo stati proprio noi, in quanto riesce a decodificarlo con la nostra chiave pubblica (che lui possiede) solo se lo abbiamo codificato noi con la nostra chiave segreta (che solo noi possediamo).
Questo piccolo (!) accorgimento è di fatto una firma, la nostra firma.
10
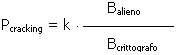
Firma Digitale e Non
Cracking: l'arte della spudoratezza
Le entità aliene, pur di leggere il contenuto dei messaggi scambiati in modo protetto tra le entità di un gruppo, possono adottare vari stratagemmi matematici, per capire il tipo di crittografia utilizzato, e possibilmente le chiavi utilizzate. Questi stratagemmi sono noti come meccanismi di cracking.
La probabilità di successo di un meccanismo di cracking è:
direttamente proporzionale alla bravura matematica dell'entità aliena
inversamente proporzionale alla bravura matematica di chi ha studiato la funzione di crittografia (ovvero il crittografo).
Se vogliamo esprimere la cosa matematicamente:
dove 'k' è una costante.
Per quanto riguarda la crittografia simmetrica bisogna considerare che l'entità aliena può sproteggere i messaggi codificati catturando le chiavi al momento della loro trasmissione tra le varie entità del gruppo. A questo riguardo bisogna dire che nel corso degli anni sono stati sviluppati e messi a punto vari meccanismi di distribuzione delle chiavi, ma tutti con una dose di rischio non nulla.
Nel caso della crittografia asimmetrica invece il problema della distribuzione delle chiavi non si pone, ma purtroppo i matematici sono come il diavolo: fanno le pentole ma non sempre si ricordano di fare anche i coperchi.
Le funzioni per la crittografia asimmetrica si basano sulla teoria dei numeri primi, e l'unico tentativo di cracking che si può mettere in atto è quello di operare con tecniche di fattorizzazione (che permettono di trovare tutti i numeri primi per cui è divisibile la chiave pubblica).
11
Firma Digitale e Non
La fattorizzazione è un processo la cui efficienza diminuisce molto rapidamente al crescere della dimensione della chiave, e poiché sinora nessuno ha messo a punto un algoritmo di fattorizzazione efficiente per grandi numeri il trucco (!) è quello di utilizzare chiavi di grandi dimensioni.
Agli albori della crittografia asimmetrica (inizio degli anni '80) i numeri decimali di cento e più cifre erano praticamente non fattorizzabili con i computer di allora. Cento cifre decimali corrispondono, grosso modo, a 512
bit, per cui inizialmente si utilizzavano chiavi a 512 bit. Con l'aumentare della potenza di calcolo dei computer, e con la diffusione di personal computer sempre più potenti, il fattore di rischio è aumentato, e si è così passati a chiavi da 1024, 2048 e 4096 bit.
Ovviamente non tutte le entità aliene sono così brave matematicamente da cimentarsi in laboriosi tentativi di fattorizzazione. Ma sproteggere il contenuto dei messaggi trasmessi non è l'unico modo di turbare il processo comunicativo di un gruppo. Anche alterare il normale scambio di messaggi, riuscendo a farsi passare per una entità amica, è un modo efficace di violare il normale scambio di messaggi.
Poiché la crittografia asimmetrica richiede che le chiavi pubbliche siano effettivamente tali, e quindi conosciute a tutti, il problema si sposta sul piano della certificazione, ovvero di meccanismi che permettono di distribuire le chiavi pubbliche associate in modo sicuro al nominativo dell'entità che le ha generate e a cui corrispondono.
Qui, per fortuna, ci vengono in aiuto gli standard di comunicazione, e in particolare gli standard della cosidetta pila ISO/OSI. In particolare il gruppo di standard denominato X.500, che copre le problematiche dello scambio di messaggi in una rete. Il nono standard di questa serie (X.509) definisce una sorta di certificato di identità elettronico, ovvero un file costituito da un certo numero di campi, che permettono di conoscere con ragionevole certezza l'identità di una entità e la relativa chiave pubblica: il tutto certificato da una entità super-partes che svolge una funzione di notaio, ovvero attesta che quanto riportato nel certificato corrisponde a verità, una entità che chiamiamo Autorità Certificante (o più comunemente, con il termine inglese Certification Authority).
Cosa garantisce che è stata proprio la nostra Certification Authority a rilasciare il certificato di un'altra entità? Il fatto che la Certification Authority ha firmato il certificato con la propria chiave segreta, e ha accluso al certificato il proprio nominativo e la propria chiave pubblica (in parole povere il proprio certificato, ovvero un documento elettronico in cui la Certification Authority attesta di essere proprio lei - un inizio ci dovrà pur essere!).
Ovviamente il certificato della Certification Authority dovrà essere distribuito a tutti (reso pubblico) in modo certo e garantito. Ma chi garantisce tutto ciò? Un'altra autorità? Ma allora non si finisce più.
Come diceva il buon vecchio Shannon la sicurezza assoluta non esiste, a meno di non utilizzare una quantità infinita di informazione ridondante per certificare il tutto. Ma ahimè, noi siamo finiti ...4
4 Almeno per ora!
12





Firma Digitale e Non