ate value. We will return to the topic of dispatch functions several times throughout this chapter.
The point of exhibiting the functional representation of a pair is not that Python actually works this way (tuples
are implemented more directly, for efficiency reasons) but that it could work this way. The functional representa-
tion, although obscure, is a perfectly adequate way to represent pairs, since it fulfills the only conditions that pairs
need to fulfill. This example also demonstrates that the ability to manipulate functions as values automatically
provides us the ability to represent compound data.
2.3 Sequences
A sequence is an ordered collection of data values. Unlike a pair, which has exactly two elements, a sequence can
have an arbitrary (but finite) number of ordered elements.
The sequence is a powerful, fundamental abstraction in computer science. For example, if we have sequences,
we can list every student at Berkeley, or every university in the world, or every student in every university. We can
8


list every class ever taken, every assignment ever completed, every grade ever received. The sequence abstraction
enables the thousands of data-driven programs that impact our lives every day.
A sequence is not a particular abstract data type, but instead a collection of behaviors that different types share.
That is, there are many kinds of sequences, but they all share certain properties. In particular,
Length. A sequence has a finite length.
Element selection. A sequence has an element corresponding to any non-negative integer index less than its
length, starting at 0 for the first element.
Unlike an abstract data type, we have not stated how to construct a sequence. The sequence abstraction is a
collection of behaviors that does not fully specify a type (i.e., with constructors and selectors), but may be shared
among several types. Sequences provide a layer of abstraction that may hide the details of exactly which sequence
type is being manipulated by a particular program.
In this section, we develop a particular abstract data type that can implement the sequence abstraction. We
then introduce built-in Python types that also implement the same abstraction.
2.3.1 Nested Pairs
For rational numbers, we paired together two integer objects using a two-element tuple, then showed that we could
implement pairs just as well using functions. In that case, the elements of each pair we constructed were integers.
However, like expressions, tuples can nest. Either element of a pair can itself be a pair, a property that holds true
for either method of implementing a pair that we have seen: as a tuple or as a dispatch function.
A standard way to visualize a pair --- in this case, the pair (1,2) --- is called box-and-pointer notation.
Each value, compound or primitive, is depicted as a pointer to a box. The box for a primitive value contains a
representation of that value. For example, the box for a number contains a numeral. The box for a pair is actually
a double box: the left part contains (an arrow to) the first element of the pair and the right part contains the second.
This Python expression for a nested tuple,
>>> ((1, 2), (3, 4))
((1, 2), (3, 4))
would have the following structure.
Our ability to use tuples as the elements of other tuples provides a new means of combination in our program-
ming language. We call the ability for tuples to nest in this way a closure property of the tuple data type. In
general, a method for combining data values satisfies the closure property if the result of combination can itself
be combined using the same method. Closure is the key to power in any means of combination because it permits
us to create hierarchical structures --- structures made up of parts, which themselves are made up of parts, and so
on. We will explore a range of hierarchical structures in Chapter 3. For now, we consider a particularly important
structure.
9

2.3.2 Recursive Lists
We can use nested pairs to form lists of elements of arbitrary length, which will allow us to implement the sequence
abstraction. The figure below illustrates the structure of the recursive representation of a four-element list: 1, 2,
3, 4.
The list is represented by a chain of pairs. The first element of each pair is an element in the list, while the
second is a pair that represents the rest of the list. The second element of the final pair is None, which indicates
that the list has ended. We can construct this structure using a nested tuple literal:
>>> (1, (2, (3, (4, None))))
(1, (2, (3, (4, None))))
This nested structure corresponds to a very useful way of thinking about sequences in general, which we have
seen before in the execution rules of the Python interpreter. A non-empty sequence can be decomposed into:
• its first element, and
• the rest of the sequence.
The rest of a sequence is itself a (possibly empty) sequence. We call this view of sequences recursive, because
sequences contain other sequences as their second component.
Since our list representation is recursive, we will call it an rlist in our implementation, so as not to confuse
it with the built-in list type in Python that we will introduce later in this chapter. A recursive list can be
constructed from a first element and the rest of the list. The value None represents an empty recursive list.
>>> empty_rlist = None
>>> def make_rlist(first, rest):
"""Make a recursive list from its first element and the rest."""
return (first, rest)
>>> def first(s):
"""Return the first element of a recursive list s."""
return s[0]
>>> def rest(s):
"""Return the rest of the elements of a recursive list s."""
return s[1]
These two selectors, one constructor, and one constant together implement the recursive list abstract data
type. The single behavior condition for a recursive list is that, like a pair, its constructor and selectors are inverse
functions.
• If a recursive list s was constructed from element f and list r, then first(s) returns f, and rest(s)
returns r.
We can use the constructor and selectors to manipulate recursive lists.
>>> counts = make_rlist(1, make_rlist(2, make_rlist(3, make_rlist(4, empty_rlist))))
>>> first(counts)
1
>>> rest(counts)
(2, (3, (4, None)))
10

Recall that we were able to represent pairs using functions, and therefore we can represent recursive lists using
functions as well.
The recursive list can store a sequence of values in order, but it does not yet implement the sequence ab-
straction. Using the abstract data type we have defined, we can implement the two behaviors that characterize a
sequence: length and element selection.
>>> def len_rlist(s):
"""Return the length of recursive list s."""
length = 0
while s != empty_rlist:
s, length = rest(s), length + 1
return length
>>> def getitem_rlist(s, i):
"""Return the element at index i of recursive list s."""
while i > 0:
s, i = rest(s), i - 1
return first(s)
Now, we can manipulate a recursive list as a sequence:
>>> len_rlist(counts)
4
>>> getitem_rlist(counts, 1)
# The second item has index 1
2
Both of these implementations are iterative. They peel away each layer of nested pair until the end of the list
(in len_rlist) or the desired element (in getitem_rlist) is reached.
The series of environment diagrams below illustrate the iterative process by which getitem_rlist finds
the element 2 at index 1 in the recursive list. First, the function getitem_rlist is called, creating a local
frame.
The expression in the while header evaluates to true, which causes the assignment statement in the while
suite to be executed.
11
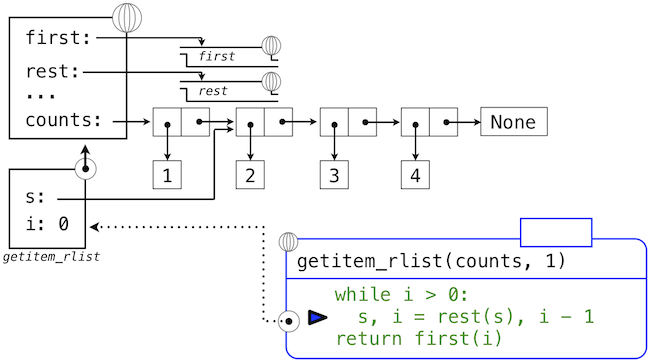

In this case, the local name s now refers to the sub-list that begins with the second element of the original list.
Evaluating the while header expression now yields a false value, and so Python evaluates the expression in the
return statement on the final line of getitem_rlist.
This final environment diagram shows the local frame for the call to first, which contains the name s
bound to that same sub-list. The first function selects the value 2 and returns it, completing the call to
getitem_rlist.
This example demonstrates a common pattern of computation with recursive lists, where each step in an
iteration operates on an increasingly shorter suffix of the original list. This incremental processing to find the
length and elements of a recursive list does take some time to compute. (In Chapter 3, we will learn to characterize
the computation time of iterative functions like these.) Python’s built-in sequence types are implemented in a
different way that does not have a large computational cost for computing the length of a sequence or retrieving
its elements.
The way in which we construct recursive lists is rather verbose. Fortunately, Python provides a variety of built-
in sequence types that provide both the versatility of the sequence abstraction, as well as convenient notation.
2.3.3 Tuples II
In fact, the tuple type that we introduced to form primitive pairs is itself a full sequence type. Tuples provide
substantially more functionality than the pair abstract data type that we implemented functionally.
12
Tuples can have arbitrary length, and they exhibit the two principal behaviors of the sequence abstraction:
length and element selection. Below, digits is a tuple with four elements.
>>> digits = (1, 8, 2, 8)
>>> len(digits)
4
>>> digits[3]
8
Additionally, tuples can be added together and multiplied by integers. For tuples, addition and multiplication
do not add or multiply elements, but instead combine and replicate the tuples themselves. That is, the add function
in the operator module (and the + operator) returns a new tuple that is the conjunction of the added arguments.
The mul function in operator (and the * operator) can take an integer k and a tuple and return a new tuple that
consists of k copies of the tuple argument.
>>> (2, 7) + digits * 2
(2, 7, 1, 8, 2, 8, 1, 8, 2, 8)
Mapping. A powerful method of transforming one tuple into another is by applying a function to each element
and collecting the results. This general form of computation is called mapping a function over a sequence, and
corresponds to the built-in function map. The result of map is an object that is not itself a sequence, but can be
converted into a sequence by calling tuple, the constructor function for tuples.
>>> alternates = (-1, 2, -3, 4, -5)
>>> tuple(map(abs, alternates))
(1, 2, 3, 4, 5)
The map function is important because it relies on the sequence abstraction: we do not need to be concerned
about the structure of the underlying tuple; only that we can access each one of its elements individually in order
to pass it as an argument to the mapped function (abs, in this case).
2.3.4 Sequence Iteration
Mapping is itself an instance of a general pattern of computation: iterating over all elements in a sequence. To
map a function over a sequence, we do not just select a particular element, but each element in turn. This pattern
is so common that Python has an additional control statement to process sequential data: the for statement.
Consider the problem of counting how many times a value appears in a sequence. We can implement a function
to compute this count using a while loop.
>>> def count(s, value):
"""Count the number of occurrences of value in sequence s."""
total, index = 0, 0
while index < len(s):
if s[index] == value:
total = total + 1
index = index + 1
return total
>>> count(digits, 8)
2
The Python for statement can simplify this function body by iterating over the element values directly, with-
out introducing the name index at all. For example (pun intended), we can write:
>>> def count(s, value):
"""Count the number of occurrences of value in sequence s."""
total = 0
for elem in s:
if elem == value:
total = total + 1
return total
13
>>> count(digits, 8)
2
A for statement consists of a single clause with the form:
for <name> in <expression>:
<suite>
A for statement is executed by the following procedure:
1. Evaluate the header <expression>, which must yield an iterable value.
2. For each element value in that sequence, in order:
A. Bind <name> to that value in the local environment.
B. Execute the <suite>.
Step 1 refers to an iterable value. Sequences are iterable, and their elements are considered in their sequential
order. Python does include other iterable types, but we will focus on sequences for now; the general definition of
the term “iterable” appears in the section on iterators in Chapter 4.
An important consequence of this evaluation procedure is that <name> will be bound to the last element of
the sequence after the for statement is executed. The for loop introduces yet another way in which the local
environment can be updated by a statement.
Sequence unpacking. A common pattern in programs is to have a sequence of elements that are themselves
sequences, but all of a fixed length. For statements may include multiple names in their header to “unpack” each
element sequence into its respective elements. For example, we may have a sequence of pairs (that is, two-element
tuples),
>>> pairs = ((1, 2), (2, 2), (2, 3), (4, 4))
and wish to find the number of pairs that have the same first and second element.
>>> same_count = 0
The following for statement with two names in its header will bind each name x and y to the first and second
elements in each pair, respectively.
>>> for x, y in pairs:
if x == y:
same_count = same_count + 1
>>> same_count
2
This pattern of binding multiple names to multiple values in a fixed-length sequence is called sequence un-
packing; it is the same pattern that we see in assignment statements that bind multiple names to multiple values.
Ranges. A range is another built-in type of sequence in Python, which represents a range of integers. Ranges
are created with the range function, which takes two integer arguments: the first number and one beyond the last
number in the desired range.
>>> range(1, 10)
# Includes 1, but not 10
range(1, 10)
Calling the tuple constructor on a range will create a tuple with the same elements as the range, so that the
elements can be easily inspected.
>>> tuple(range(5, 8))
(5, 6, 7)
If only one argument is given, it is interpreted as one beyond the last value for a range that starts at 0.
>>> tuple(range(4))
(0, 1, 2, 3)
14
Ranges commonly appear as the expression in a for header to specify the number of times that the suite
should be executed:
>>> total = 0
>>> for k in range(5, 8):
total = total + k
>>> total
18
A common convention is to use a single underscore character for the name in the for header if the name is
unused in the suite:
>>> for _ in range(3):
print(’Go Bears!’)
Go Bears!
Go Bears!
Go Bears!
Note that an underscore is just another name in the environment as far as the interpreter is concerned, but has
a conventional meaning among programmers that indicates the name will not appear in any expressions.
2.3.5 Sequence Abstraction
We have now introduced two types of native data types that implement the sequence abstraction: tuples and ranges.
Both satisfy the conditions with which we began this section: length and element selection. Python includes two
more behaviors of sequence types that extend the sequence abstraction.
Membership. A value can be tested for membership in a sequence. Python has two operators in and not
in that evaluate to True or False depending on whether an element appears in a sequence.
>>> digits
(1, 8, 2, 8)
>>> 2 in digits
True
>>> 1828 not in digits
True
All sequences also have methods called index and count, which return the index of (or count of) a value in
a sequence.
Slicing. Sequences contain smaller sequences within them. We observed this property when developing our
nested pairs implementation, which decomposed a sequence into its first element and the rest. A slice of a sequence
is any span of the original sequence, designated by a pair of integers. As with the range constructor, the first
integer indicates the starting index of the slice and the second indicates one beyond the ending index.
In Python, sequence slicing is expressed similarly to element selection, using square brackets. A colon sep-
arates the starting and ending indices. Any bound that is omitted is assumed to be an extreme value: 0 for the
starting index, and the length of the sequence for the ending index.
>>> digits[0:2]
(1, 8)
>>> digits[1:]
(8, 2, 8)
Enumerating these additional behaviors of the Python sequence abstraction gives us an opportunity to reflect
upon what constitutes a useful data abstraction in general. The richness of an abstraction (that is, how many
behaviors it includes) has consequences. For users of an abstraction, additional behaviors can be helpful. On the
other hand, satisfying the requirements of a rich abstraction with a new data type can be challenging. To ensure
that our implementation of recursive lists supported these additional behaviors would require some work. Another
negative consequence of rich abstractions is that they take longer for users to learn.
15
Sequences have a rich abstraction because they are so ubiquitous in computing that learning a few complex
behaviors is justified. In general, most user-defined abstractions should be kept as simple as possible.
Further reading. Slice notation admits a variety of special cases, such as negative starting values, ending
values, and step sizes. A complete description appears in the subsection called slicing a list in Dive Into Python 3.
In this chapter, we will only use the basic features described above.
2.3.6 Strings
Text values are perhaps more fundamental to computer science than even numbers. As a case in point, Python
programs are written and stored as text. The native data type for text in Python is called a string, and corresponds
to the constructor str.
There are many details of how strings are represented, expressed, and manipulated in Python. Strings are
another example of a rich abstraction, one which requires a substantial commitment on the part of the programmer
to master. This section serves as a condensed introduction to essential string behaviors.
String literals can express arbitrary text, surrounded by either single or double quotation marks.
>>> ’I am string!’
’I am string!’
>>> "I’ve got an apostrophe"
"I’ve got an apostrophe"
>>> ’??’
’??’
We have seen strings already in our code, as docstrings, in calls to print, and as error messages in assert
statements.
Strings satisfy the two basic conditions of a sequence that we introduced at the beginning of this section: they
have a length and they support element selection.
>>> city = ’Berkeley’
>>> len(city)
8
>>> city[3]
’k’
The elements of a string are themselves strings that have only a single character. A character is any single letter
of the alphabet, punctuation mark, or other symbol. Unlike many other programming languages, Python does not
have a separate character type; any text is a string, and strings that represent single characters have a length of 1.
Like tuples, strings can also be combined via addition and multiplication.
>>> ’Berkeley’ + ’, CA’
’Berkeley, CA’
>>> ’Shabu ’ * 2
’Shabu Shabu ’
Membership. The behavior of strings diverges from other sequence types in Python. The string abstraction
does not conform to the full sequence abstraction that we described for tuples and ranges. In particular, the mem-
bership operator in applies to strings, but has an entirely different behavior than when it is applied to sequences.
It matches substrings rather than elements.
>>> ’here’ in "Where’s Waldo?"
True
Likewise, the count and index methods on strings take substrings as arguments, rather than single-character
elements. The behavior of count is particularly nuanced; it counts the number of non-overlapping occurrences
of a substring in a string.
>>> ’Mississippi’.count(’i’)
4
>>> ’Mississippi’.count(’issi’)
1
16
Multiline Literals. Strings aren’t limited to a single line. Triple quotes delimit string literals that span multiple
lines. We have used this triple quoting extensively already for docstrings.
>>> """The Zen of Python
claims, Readability counts.
Read more: import this."""
’The Zen of Python\nclaims, "Readability counts."\nRead more: import this.’
In the printed result above, the \n (pronounced “backslash en”) is a single element that represents a new line.
Although it appears as two characters (backslash and “n”), it is considered a single character for the purposes of
length and element selection.
String Coercion. A string can be created from any object in Python by calling the str constructor function
with an object value as its argument. This feature of strings is useful for constructing descriptive strings from
objects of various types.
>>> str(2) + ’ is an element of ’ + str(digits)
’2 is an element of (1, 8, 2, 8)’
The mechanism by which a single str function can apply to any type of argument and return an appropriate
value is the subject of the later section on generic functions.
Methods. The behavior of strings in Python is extremely productive because of a rich set of methods for
returning string variants and searching for contents. A few of these methods are introduced below by example.
>>> ’1234’.isnumeric()
True
>>> ’rOBERT dE nIRO’.swapcase()
’Robert De Niro’
>>> ’snakeyes’.upper().endswith(’YES’)
True
Further reading. Encoding text in computers is a complex topic. In this chapter, we will abstract away the
details of how strings are represented. However, for many applications, the particular details of how strings are
encoded by computers is essential knowledge. Sections 4.1-4.3 of Dive Into Python 3 provides a description of character encodings and Unicode.
2.3.7 Conventional Interfaces
In working with compound data, we’ve stressed how data abstraction permits us to design programs without
becoming enmeshed in the details of data representations, and how abstraction preserves for us the flexibility to
experiment with alternative representations. In this section, we introduce another powerful design principle for
working with data structures --- the use of conventional interfaces.
A conventional interface is a data format that is shared across many modular components, which can be mixed
and matched to perform data processing. For example, if we have several functions that all take a sequence as
an argument and return a sequence as a value, then we can apply each to the output of the next in any order we
choose. In t









