Parallel Manipulators Towards New Applications by Huapeng Wu - HTML preview

!

KndNKffector

C

B

A

x

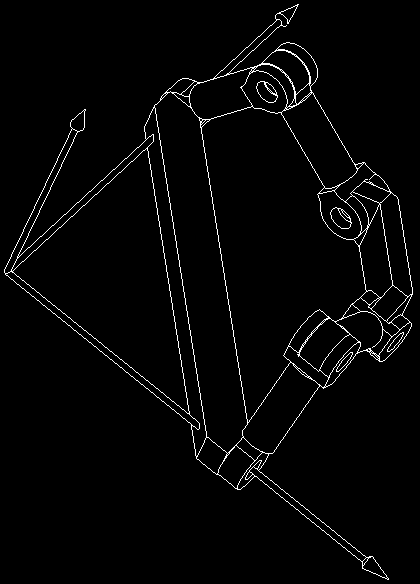
Fig. 10 a Spatial Six-Link Mechanism with a Straight line Translational End-Effector

From the above analysis, it is not difficult to find that the two kinematic chains ,0+ and

4#D can surely guarantee the pure straight line translation of the end-effector +D so long

as $,0+ and $4#D do not descend in ranks. To analyze the sensitivity of the structure stability to the angle @ , one should turn to the equations (37) and (38) and investigate the

resultant terminal constraints, which can be expressed with:

)1 cos@

0

0 0&

'

$

'0 sin@

0

0 0$

+

'0

0

0

0 0$

+D

$

!@"# '

$

(47)

'0

0

sin@

0 0$

'

$

0

0

2

@

'

cos

1 0$

'(0

0

0

0 1$%

'

.

where cos@ #

and sin@ #

.

2

2

2

2

' 6 .

' 6 .

If the terminal constraints denoted by +

+D

$

!@" are well conditioned, the mechanism will

have fine structure stability. From equations (29) and (47), one can find that the end-effector

will have one straight line translation along

+

3 -axis so long as

1

!'$( $+D !@ ",.

/

# 5 , which can

0

-

be immediately transformed to investigate the following sub matrix of +

+D

$

!@":

490

Parallel Manipulators, Towards New Applications

)1 cos@

0

0 0&

'

$

'0 sin@

0

0 0$

!

, @ " # '0

0

sin@

0 0$

'

$

'0

0

2 cos@ 1 0$

'

$

(0

0

0

0 1%

Letting 467! !

, @ " # 0 , one immediately obtains @ # 0 or @ # G . Therefore, in order to keep

the end-effector +D have one straight line translation along 3 -axis, there will be @ 3 0 and

@ 3 G . So, the rigid guidance mechanism synthesized in this chapter has a wider adaptation

of angle between the planes of its two kinematic chains. Now, the sensitivity of the structure

stability to the angle @ of the mechanism can be judged by the condition number of matrix

!

, @ " (Kelley, 1995). Let

1 " .

Hm89/ , , ,

-H$)! , "

1

0

-

#

2

,

,

#

1

2

#

(48)

2

2

1 " .

min

H

/ , , ,

0

-

where -H$)! , "2 indicates the condition number of matrix , , , indicates the 2-norm of

2

matrix

"

"

, , and 1

H , , ,.

/

indicates the eigenvalues of matrix , , .

0

-

y

K

z

F

D

KndNKffector

o

C

B

A

x

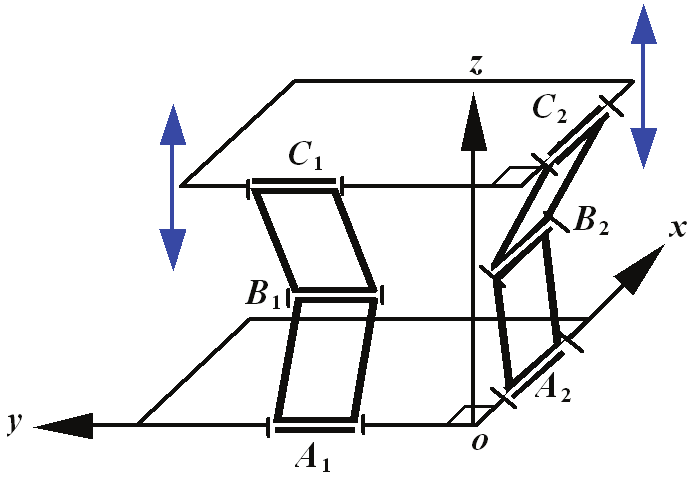
Fig. 11 a Spatial Six-Link Mechanism with the Best Structure Stability

The solution of equation (48) is:

G

@ #

(49)

2

Mo9ility of <patial Paral el Manipulators

491

Equation (49) indicates that the mechanism will have the best structure stability when

G

@ # , which is shown in Fig. 11. Compared with Peaucellier-Lipkin eight-link linkage, the

2

spatial six-link mechanism synthesized in this chapter has the least links and revolute joints,

and the whole end-effector +D can make an exact straight line translation while Peaucellier-

Lipkin eight-link linkage can only allow one specified point to make such a motion.

As a matter of fact, the mechanism shown in Fig. 11 is a Sarrus linkage. However, the

mechanism proposed here does not necessarily require that the two kinematic chains must

within two orthogonal planes which are needed for Sarrus linkage. The so-called Sarrus

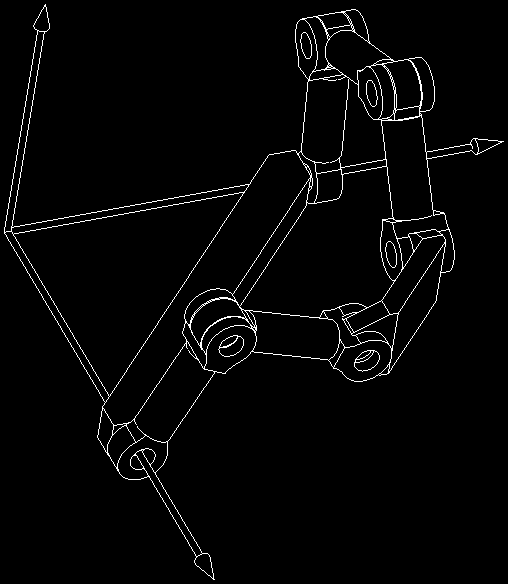
linkage, which is shown in Fig. 12, is a linkage that converts circular motion to linear motion

by using hinged squares. The square end-effector 1

+ + 2 can make an exact straight line

translation along 3 -axis which shows better properties both in mechanical structure and in

kinematics than those of Peaucellier-Lipkin eight-link linkage. However, because of the

limited workspace and the uneconomic mechanism architecture, the restrictions of Sarrus

linkage shown in Fig. 12 compared with the one shown in Fig. 11 are obvious.

Fig. 12 the Structure of Sarrus Linkage

z

K

D

F

y

o

G

KndNKffector

B

C

A

x

Fig. 13 Configuration of the Spatial Seven-Link Mechanism

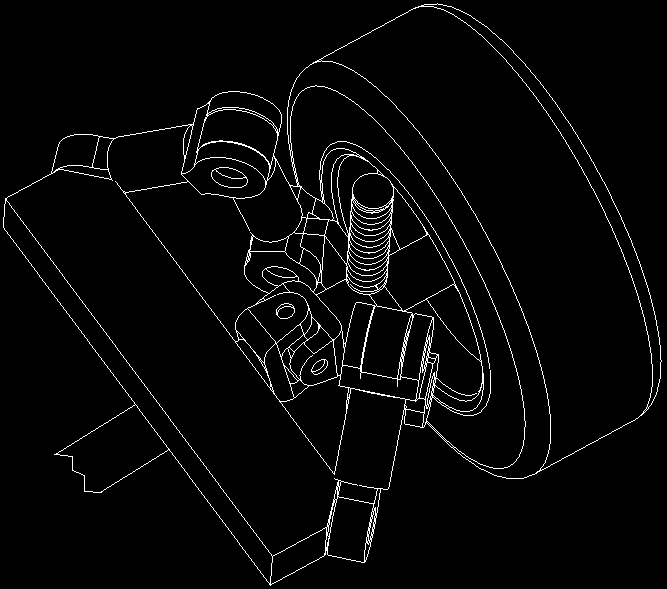
492

Parallel Manipulators, Towards New Applications

As mentioned in step 6, in order to keep the twists of the chain to be equivalent to the twist

basis, the rank of the twists of each kinematic chain synthesized through equation (34)

should equal the dimension of its twist basis. Therefore, if one or more such twists are

added to each kinematic chain, the free motions of the end-effector will not be changed. As

an example, the mechanism shown in Fig. 13 is the derivative form of that in Fig. 10 by

adding one twist 1

I

$ to the kinematic chain 4#D . Where

$ # 0 1 0 2 3

0 2

I

!

I

" "

I

The two kinematic chains of the end-effector +D are now changed to be ,0+ and 4#I D

1

.

The twists of them two are:

; $

# $

$

$

,0+

B ,4 04 +4

1

1

1

C

:

9 $

# $

$

$

$

4#ID

B 44 #4 I4 D4

2

2

2

2

C

It is not difficult to find that the terminal constraints of kinematic chains ,0+ and 4#I D

1

are still expressed by equation (36). And therefore, the free motion of the end-effector +D is

still a straight line translation along 3 -axis shown in Fig. 13. As a result, the free motions of

the end-effector will not be changed if one or more revolute joints whose Pl cker

coordinates have the form of equation (44) are added in the second kinematic chain.

Similarly, the free motions of the end-effector will not be changed either if one or more

revolute joints whose Pl cker coordinates have the form of equation (41) are added to the

first kinematic chain.

Steering rod

KndNKffector

Aehicle Body

:heel

:heel

Transmission Axles

Left: Front Suspension Right: Rear Suspension

Fig. 14 a Front Suspension and a Rear Suspension

Mo9ility of <patial Paral el Manipulators

493

For engineering applications, the end-effector +D in Fig. 11 or Fig. 13 can be utilized as the

guiding equipment of a mechanism that requires a precise linear translation, such as the

independent suspension of automobile. Because the end-effector of the rigid guidance

mechanism can make an exact straight line translation, the front and rear suspensions made

up of such a mechanism shown in Fig. 14 allow the orientation and position parameters of

the wheels such as kingpin, caster, camber, and axes distance and wheel track to be

constant. These merits not only enhance the ride and handling of the vehicles, but also

reduce the wearing of the tires during jounce and rebound.

D5#E%28(34'%2#

This chapter focuses on the mobility analysis and synthesis of spatial parallel manipulators.

It focuses on developing an analytical methodology to investigate the instantaneous DOF of

the end-effector of a parallel manipulator and the instantaneous controllability of the end-

effector from the viewpoint of the possible actuation schemes for the parallel manipulator.

Via comparing the differences and essential mobility of a set of underactuated, over

actuated and equally actuated manipulators, this chapter demonstrates that the

underactuated, over actuated and fully actuated manipulators are all substantially equally

actuated mechanisms. This work is significantly important for a designer to contrive his or

her manipulators with underactuated or over actuated structures. Based on the analytical

model of the DOF of a spatial parallel manipulator, this chapter also investigates a general

process to synthesize the manipulators with specified mobility. The outstanding

characteristics of the synthesis method are that the whole process is also analytical and each

step can be programmed at a computer. Because of the restrictions of the traditional general

mobility formulas for spatial mechanisms, a lot of mechanisms that might not be

synthesized directly with the general mobility formulas could be synthesized with this

analytical theory of degrees of freedom for spatial mechanisms.

F5#G8H2%C(17;1<12)4#

This research was supported by FANEDD under Grant 200741 and the National Natural

Science Foundation of China under Grant 50425516. The authors gratefully acknowledge

these support agencies.

I5#J1+1012814#

Arsenault, M. & Boudreau, R. (2006). Synthesis of Planar Parallel Mechanisms While

Considering Workspace, Dexterity, Stiffness and Singularity Avoidance, ASME

Journal of Mechanical Design, Vol. 128, No. 1, (January, 2006)69-78 ISSN: 1050-0472

Ball, R. S. (First Published 1900, Reprinted 1998). a Treatise on the Theory of Screws,

Cambridge University Press, ISBN 0-521-63650-7, Cambridge

Birglen, L. & Gosselin, C. M. (2006a). Geometric Design of Three-Phalanx Underactuated

Fingers, ASME Journal of Mechanical Design, Vol. 128, No. 2, (March 2006)356-364,

ISSN: 1050-0472

494

Parallel Manipulators, Towards New Applications

Birglen, L. & Gosselin, C. M. (2006b). Grasp-state plane analysis of two-phalanx

underactuated fingers, Mechanism and Machine Theory, Vol. 41, No. 7, (July

2006)807-822, ISSN: 0094-114n

Chakraborty, N. & Ghosal, A. (2004). Kinematics of Wheeled Mobile Robots on Uneven

Terrain, Mechanism and Machine Theory, Vol. 39, No. 12, (December 2004)1273-

1287, ISSN: 0094-114n

Dai, J. S. & Jones, J. Rees. (1999). Mobility in Metamorphic Mechanisms of

Foldable/Erectable Kinds, ASME Journal of Mechanical Design, Vol. 121, No. 3,

(1999)375-382, ISSN: 1050-0472

Gogu, G. (2005a). Mobility of Mechanisms: a Critical Review. Mechanism and Machine

Theory, Vol. 40, No. 9, (September 2005) 1068-1097, ISSN: 0094-114n

Gogu, G. (2005b). Mobility and Spatiality of Parallel Robots Revisited via Theory of Linear

Transformations, European Journal of Mechanics A/Solids, Vol. 24, No. 4, (July-

August 2005) 690-711, ISSN: 0997-7538

Gosselin, C. M. & Lalibertd, C. T. (1998). Underactuated Mechanical Finger with Return

Actuation , Patent Number: 5762390, Date of Patent: June 9, 1998,

http://robot.gmc.ulaval.ca/en/publi/patents.html.

Huang, *.; Kong, L. F. & Fang, Y. F. (1997). Theory of Mechanism of Parallel Robotics and

Control, Machinery Industry Press, ISBN: 7-111-05812-7, Beijing

Huang, *.; *hao, Y. S. & *hao, T. S. (2006). Advanced Spatial Mechanism, Advanced

Educational Press of China, ISBN:7-04-019265-9, Beijing

Hunt, K. H. (1978). Kinematic Geometry of Mechanisms, Oxford University Press, ISBN 0-

19-856124-5, Oxford

Jain, A. & Rodriguez, G. (1993) An Analysis of the Kinematics and Dynamics of

Underactuated Manipulators, IEEE Transactions on Robotics and Automation, Vol.

9, No. 4, (August 1993)411-422, ISSN: 1042-296n

Kelley, C. T. (1995). Iterative Methods for Linear and Nonlinear Equations, North Carolina

State University, Society for Industrial and Applied Mathematics, ISBN:

0898713528(pbk.), Philadelphia

Kempe, A. B. (1877). How to Draw a Straight Line, London: Macmillan. Cited by Henderson,

D. W. & Taimina, D., http://kmoddl.library.cornell.edu/tutorials/11/.

Kumar, V. (1992). Instantaneous Kinematics of Parallel-Chain Robotic Mechanisms, ASME

Journal of Mechanical Design, Vol. 114, (September 1992)349-358, ISSN: 0738-0666

Lalibertd, T. & Gosselin, C. M. (1998). Simulation and Design of Underactuated Mechanical

Hands, Mechanism and Machine Theory, Vol. 33, No. 1-2, (January-February

1998)39-57, ISSN: 0094-114n

Murakami, T. et al. (1989). Development of a new multi-link front suspension, SAE 890179.

Phillips, J. (1984). Freedom in Machinery, Vol. 1: Introducing Screw Theory, Cambridge

University Press, ISBN 0-521-23696-7, Cambridge

Phillips, J. (1990). Freedom in Machinery, Vol. 2: Screw Theory Exemplified, Cambridge

University Press, ISBN 0-521-25442-6, Cambridge

Mo9ility of <patial Paral el Manipulators

495

Phillips, J. R. & Hunt, K. H. (1964). On the Theorem of Three Axes in the Spatial Motion of

Three Bodies, Australian Journal of Applied Science, Vol. 15, (1964) 267-287, ISSN:

0572-1156

Raghavan, M. (1996). Number and Dimensional Synthesis of Independent Suspension

Mechanisms, Mechanism and Machine Theory, Vol. 31, No. 8, (November,

1996)1141-1153, ISSN: 0094-114n

Raghavan, M. (2005). Suspension Synthesis for N:1 Roll Center Motion, ASME Journal of

Mechanical Design, Vol. 127, No. 4, (July 2005) 673-678, ISSN: 1050-0472

Rotman, Joseph J. (2002). Advanced Modern Algebra, Prentice Hall, (May 2002) ISBN :

0130878685

Shigley, J. E. & Uicker, J. J. (1980). Theory of Machines and Mechanisms, New York:

McGraw-Hill Companies, Inc. , ISBN: 0070568847, New York

Simionescu, P. A. & Beale, D. (2002). Synthesis and Analysis of the Five-Link Rear

Suspension System Used in Automobiles, Mechanism and Machine Theory, Vol. 37,

No. 9, (September, 2002)815-832, ISSN: 0094-114n

Suh, C. H. (1989). Synthesis and analysis of suspension mechanisms with use of

displacement matrices, SAE 890098.

Tsai, L.-W. (2001). Mechanism Design: Enumeration of Kinematic Structures According to

Function, CRC Press LLC, ISBN 0-8493-09018, Florida

Waldron, K. J. (1966). The Constraint Analysis of Mechanisms, Journal of Mechanisms, Vol.

1, (1966)101-114, ISSN: 0094-114n

Yan, H.-S. & Kuo, C.-H. (2006). Topological Representations and Characteristics of Variable

Kinematic Joints, ASME Journal of Mechanical Design, Vol. 128, No. 2, (March,

2006)384-391, ISSN: 1050-0472

Yi, B.-J. & Kim, W. K. (2002). The Kinematics for Redundantly Actuated Omnidirectional

Mobile Robots, Journal of Robotic Systems, Vol. 19, No. 6, (June 2002)255 267,

ISSN: 0741-2223

Yiu, Y. K. & Li, *. (2003). Trajectory Generation for a 2-dof Over-actuated Parallel

Manipulator with Actuator Speed and Torque Limits Consideration, Proceedings

2003 IEEE International Symposium on Computational Intelligence in Robotics and

Automation, pp.1058-1063, ISBN: 0-7803-7866, July 16-20, 2003, Kobe, Japan.

*hao, J.-S. et al. (2004a). A New Method to Study the Degree of Freedom of Spatial Parallel

Mechanisms. The International Journal of Advanced Manufacturing Technology,

Vol. 23, No. 3-4, (February 2004) 288-294, ISSN: 0268-3768

*hao, J.-S.; *hou, K. & Feng, *.-J. (2004b). A Theory of Degrees of Freedom For Mechanisms,

Mechanism and Machine Theory, Vol. 39, No. 6, (June 2004)621-643, ISSN: 0094-

114n

*hao, J.-S. et al. (2006a). Re-analysis of the Degree-of-Freedom Configuration of the

Platforms in Spatial Parallel Mechanisms with Constraints Spaces, The

International Journal of Advanced Manufacturing Technology, Vol. 28, No. 1-2,

(February 2006)190-196, ISSN: 0268-3768

496

Parallel Manipulators, Towards New Applications

*hao, J.-S. et al. (2006b). The Free Mobility of a Parallel Manipulator, Robotica, Vol.24, No.5,

(September 2006)635-641, ISSN: 0263-5747

*hao, J.-S.; Feng, *.-J. Dong, J.- n. (2006c). Computation of the Configuration Degree of

Freedom of a Spatial Parallel Mechanism by Using Reciprocal Screw Theory,

Mechanism and Machine Theory, Vol. 41, No. 12, (December 2006)1486-1504, ISSN:

0094-114n

22

Feasible Human-Spine Motion Simulators

Based on Parallel Manipulators

Si-Jun Zhu1,2, Zhen Huang2 and Ming-Yang Zhao1

1 Shenyang Institute of Automation (CMS)

2 Yanshan University

P.R. China

1. Introduction

In biological kinematics, motion of a spine is realized by a number of functional spinal units

(FSU), as shown in Fig.1 (spineuniverse.com). Each FSU consists of two adjacent vertebras

and physiological organization joining FSUs end-to-end (Hou, 2005). Owe to the spine,

vertebrates have more flexible torsos than others. To understand, simulate and utilize the

motion of vertebrate’s torso, international researchers have made many bio-vertebrate

robots such as robotic dog (bostondynamics.com), fish (robotic-fish.net), snake (Hirose;

nasa.gov; ri.cmu.edu; snakerobots.com), rabbit (jsk.t.u-tokyo.ac.jp), lizard (birg.epfl.ch) and

humanoid robot (kawada.co.jp; sony.net; world.honda.com; Giuseppe et al., 2003).

Fig. 1. A human-spine and FSU physiological organization

Torsos of some bio-vertebrate robots adopt torsos without bio-spine structure. As the most

advanced quadruped robot on Earth, BigDog (bostondynamics.com) adopted rigid torso

which result in the failure to realize the motion between shoulder and waist.

498

Parallel Manipulators, Towards New Applications

To improve flexibility, some bio-vertebrate robots adopt bio-spine torso, which means a

number of functional kinematic units (FKU, working as FSU) joined end-to-end through

joining structure. Similar with the spine for vertebrates, the bio-spine torso enable

maneuverability of bio-vertebrate robots. High maneuverability qualifies robotic fishes for

the oceanographical observation, the leak detection on pipelines, the search for mines and <