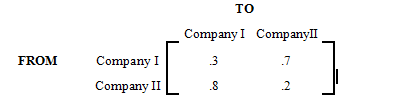
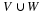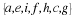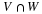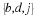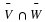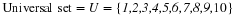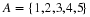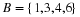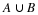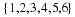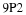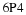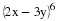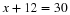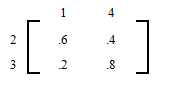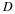Applied Finite Mathematics by Rupinder Sekhon, UniqU, LLC - HTML preview

/ Home / Mathematics / Applied Finite Mathematics
PLEASE NOTE: This is an HTML preview only and some elements such as links or page numbers may be incorrect.
Download the book in PDF, ePub, Kindle for a complete version.
PREV   NEXT

Chapter 15. More Probability

Chapter Overview

In this chapter, you will learn to:

  1. Find the probability of a binomial experiment.

  2. Find probabilities using Bayes' Formula.

  3. Find the expected value or payoff in a game of chance.

  4. Find probabilities using tree diagrams.

Binomial Probability

In this section, we will consider types of problems that involve a sequence of trials, where each trial has only two outcomes, a success or a failure. These trials are independent, that is, the outcome of one does not affect the outcome of any other trial. Furthermore, the probability of success, p, and the probability of failure, (1−p), remains the same throughout the experiment. These problems are called binomial probability problems. Since these problems were researched by a Swiss mathematician named Jacques Bernoulli around 1700, they are also referred to as Bernoulli trials.

We give the following definition:

Binomial Experiment

A binomial experiment satisfies the following four conditions:

  1. There are only two outcomes, a success or a failure, for each trial.

  2. The same experiment is repeated several times.

  3. The trials are independent; that is, the outcome of a particular trial does not affect the outcome of any other trial.

  4. The probability of success remains the same for every trial.

The probability model that we are about to investigate will give us the tools to solve many real-life problems like the ones given below.

  1. If a coin is flipped 10 times, what is the probability that it will fall heads 3 times?

  2. If a basketball player makes 3 out of every 4 free throws, what is the probability that he will make 7 out of 10 free throws in a game?

  3. If a medicine cures 80% of the people who take it, what is the probability that among the ten people who take the medicine, 6 will be cured?

  4. If a microchip manufacturer claims that only 4% of his chips are defective, what is the probability that among the 60 chips chosen, exactly three are defective?

  5. If a telemarketing executive has determined that 15% of the people contacted will purchase the product, what is the probability that among the 12 people who are contacted, 2 will buy the product?

We now consider the following example to develop a formula for finding the probability of k successes in n Bernoulli trials.

Example 15.1. 
Problem

A baseball player has a batting average of .300. If he bats four times in a game, find the probability that he will have

  1. four hits

  2. three hits

  3. two hits

  4. one hit

  5. no hits.

Let us suppose S denotes that the player gets a hit, and F denotes that he does not get a hit.

This is a binomial experiment because it meets all four conditions. First, there are only two outcomes, S or F. Clearly the experiment is repeated four times. Lastly, if we assume that the player's skillfulness to get a hit does not change each time he comes to bat, the trials are independent with a probability of .3 of getting a hit during each trial.

We draw a tree diagram to show all situations.

A Tree diagram showing the all the possible situations for this problem.
Figure 15.0. 

Let us first find the probability of getting, for example, two hits. We will have to consider the six possibilities, 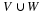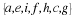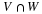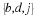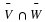_autogen-svg2png-0010.png, _autogen-svg2png-0011.png, _autogen-svg2png-0012.png, _autogen-svg2png-0013.png, _autogen-svg2png-0014.png, _autogen-svg2png-0015.png, as shown in the above tree diagram. We list the probabilities of each below.

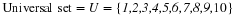
_autogen-svg2png-0016.png

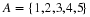
_autogen-svg2png-0017.png

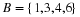
_autogen-svg2png-0018.png

_autogen-svg2png-0019.png

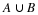
_autogen-svg2png-0020.png

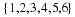
_autogen-svg2png-0021.png

Since the probability of each of these six outcomes is (.3)2(.7)2, the probability of obtaining two successes is 6(.3)2(.7)2.

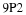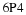The probability of getting one hit can be obtained in the same way. Since each permutation has one S and three F's, there are four such outcomes: _autogen-svg2png-0026.png, _autogen-svg2png-0027.png, _autogen-svg2png-0028.png, and _autogen-svg2png-0029.png.

And since the probability of each of the four outcomes is (.3)(.7)3, the probability of getting one hit is 4(.3)(.7)3.

The table below lists the probabilities for all cases, and shows a comparison with the binomial expansion of fourth degree. Again, p denotes the probability of success, and q=(1−p) the probability of failure.

Table 15.1.
OutcomeFour HitsThree hitsTwo HitsOne hitsNo Hits
Probability ( . 3 ) 4 4 ( . 3 ) 3 ( . 7 ) 6 ( . 3 ) 2 ( . 7 ) 2 4 ( . 3 ) ( . 7 ) 3 ( . 7 ) 4

This gives us the following theorem:

Theorem 15.1.
Binomial Probability Theorem

The probability of obtaining k successes in n independent Bernoulli trials is given by

(15.1)
_autogen-svg2png-0041.png

where p denotes the probability of success and q=(1−p)the probability of failure.

We use the above formula to solve the following examples.

Example 15.2. 
Problem

If a coin is flipped 10 times, what is the probability that it will fall heads 3 times?

Let S denote the probability of obtaining a head, and F the probability of obtaining a tail.

Clearly, n=10, k=3, p=1/2, and q=1/2.

Therefore,

(15.2)b(10,3;1/2)=10C3(1/2)3(1/2)7=.1172
Example 15.3. 
Problem

If a basketball player makes 3 out of every 4 free throws, what is the probability that he will make 6 out of 10 free throws in a game?

The probability of making a free throw is 3/4. Therefore, p=3/4, q=1/4, n=10, and k=6.

Therefore,

(15.3)b(10,6;3/4)=10C6(3/4)6(1/4)4=.1460
Example 15.4. 
Problem

If a medicine cures 80% of the people who take it, what is the probability that of the eight people who take the medicine, 5 will be cured?

Here p=.80, q=.20, n=8, and k=5.

(15.4)b(8,5;.80)=8C5(.80)5(.20)3=.1468
Example 15.5. 
Problem

If a microchip manufacturer claims that only 4% of his chips are defective, what is the probability that among the 60 chips chosen, exactly three are defective?

If S denotes the probability that the chip is defective, and F the probability that the chip is not defective, then p=.04, q=.96, n=60, and k=3.

(15.5)b(60,3;.04)=60C3(.04)3(.96)57=.2138
Example 15.6. 
Problem

If a telemarketing executive has determined that 15% of the people contacted will purchase the product, what is the probability that among the 12 people who are contacted, 2 will buy the product?

If S denoted the probability that a person will buy the product, and F the probability that the person will not buy the product, then p=.15, q=.85, n=12, and k=2.

b(12,2,.15)=12C2(.15)2(.85)10=.2924.

Bayes' Formula

In this section, we will develop and use Bayes' Formula to solve an important type of probability problem. Bayes' formula is a method of calculating the conditional probability P(F∣E) from P(E∣F). The ideas involved here are not new, and most of these problems can be solved using a tree diagram. However, Bayes' formula does provide us with a tool with which we can solve these problems without a tree diagram.

We begin with an example.

Example 15.7. 
Problem

Suppose you are given two jars. Jar I contains one black and 4 white marbles, and Jar II contains 4 black and 6 white marbles. If a jar is selected at random and a marble is chosen,

  1. What is the probability that the marble chosen is a black marble?

  2. If the chosen marble is black, what is the probability that it came from Jar I?

  3. If the chosen marble is black, what is the probability that it came from Jar II?

Let _autogen-svg2png-0075.png I be the event that Jar I is chosen, _autogen-svg2png-0076.png be the event that Jar II is chosen, B be the event that a black marble is chosen and W the event that a white marble is chosen.

We illustrate using a tree diagram.

The figure shows that there are 2 available jars with marbles in them to choose from. The Tree diagram shows the probability of choosing either jar, while also giving the probability of choosing a white or black marble from either.
(a)
Subfigure (b) (graphics3.png)
(b)
Figure 15.0. 

  1. The probability that a black marble is chosen is P(B)=1/10+2/10=3/10.

  2. To find _autogen-svg2png-0080.png, we use the definition of conditional probability, and we get

    (15.6)
    _autogen-svg2png-0081.png

  3. Similarly, _autogen-svg2png-0082.png

    In parts b and c, the reader should note that the denominator is the sum of all probabilities of all branches of the tree that produce a black marble, while the numerator is the branch that is associated with the particular jar in question.

We will soon discover that this is a statement of Bayes' formula .

Let us first visualize the problem.

We are given a sample space

PREV   NEXT