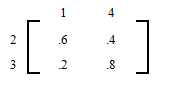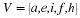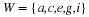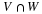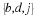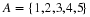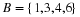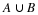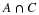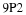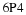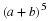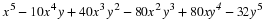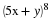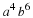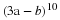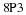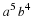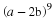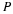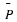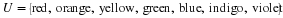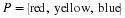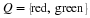In this chapter, you will learn to:
Write transition matrices for Markov Chain problems.
Find the long term trend for a Regular Markov Chain.
Solve and interpret Absorbing Markov Chains.
We will now study stochastic processes, experiments in which the outcomes of events depend on the previous outcomes. Such a process or experiment is called a Markov Chain or Markov process. The process was first studied by a Russian mathematician named Andrei A. Markov in the early 1900s.
A small town is served by two telephone companies, Mama Bell and Papa Bell. Due to their aggressive sales tactics, each month 40% of Mama Bell customers switch to Papa Bell, that is, the other 60% stay with Mama Bell. On the other hand, 30% of the Papa Bell customers switch to Mama Bell. The above information can be expressed in a matrix which lists the probabilities of going from one state into another state. This matrix is called a transition matrix.
The reader should observe that a transition matrix is always a square matrix because all possible states must have both rows and columns. All entries in a transition matrix are non-negative as they represent probabilities. Furthermore, since all possible outcomes are considered in the Markov process, the sum of the row entries is always 1.
Professor Symons either walks to school, or he rides his bicycle. If he walks to school one day, then the next day, he will walk or cycle with equal probability. But if he bicycles one day, then the probability that he will walk the next day is 1/4. Express this information in a transition matrix.
We obtain the following transition matrix by properly placing the row and column entries. Note that if, for example, Professor Symons bicycles one day, then the probability that he will walk the next day is 1/4, and therefore, the probability that he will bicycle the next day is 3/4.
In Example 17.1, if it is assumed that the first day is Monday, write a matrix that gives probabilities of a transition from Monday to Wednesday.
Let W denote that Professor Symons walks and B denote that he rides his bicycle.
We use the following tree diagram to compute the probabilities.
The probability that Professor Symons walked on Wednesday given that he walked on Monday can be found from the tree diagram, as listed below.
.
.
.
.
We represent the results in the following matrix.
Alternately, this result can be obtained by squaring the original transition matrix.
We list both the original transition matrix T and T2 as follows:
The reader should compare this result with the probabilities obtained from the tree diagram.
Consider the following case, for example,
It makes sense because to find the probability that Professor Symons will walk on Wednesday given that he bicycled on Monday, we sum the probabilities of all paths that begin with
B and end in
W. There are two such paths, and they are
and
.
The transition matrix for Example 17.1 is given below.
Write the transition matrix from a) Monday to Thursday, b) Monday to Friday.
In writing a transition matrix from Monday to Thursday, we are moving from one state to another in three steps. That is, we need to compute T3.
b) To find the transition matrix from Monday to Friday, we are moving from one state to another in 4 steps. Therefore, we compute T4.
It is important that the student is able to interpret the above matrix correctly. For example, the entry 85/128, states that if Professor Symons walked to school on Monday, then there is 85/128 probability that he will bicycle to school on Friday.
There are certain Markov chains that tend to stabilize in the long run, and they are the subject of the section called “Regular Markov Chains”. It so happens that the transition matrix we have used in all the above examples is just such a Markov chain. The next example deals with the long term trend or steady-state situation for that matrix.
Suppose Professor Symons continues to walk and bicycle according to the transition matrix given in Example 17.1. In the long run, how often will he walk to school, and how often will he bicycle?
As mentioned earlier, as we take higher and higher powers of our matrix T, it should stabilize.
Therefore, in the long run, Professor Symons will walk to school 1/3 of the time and bicycle 2/3 of the time.
When this happens, we say that the system is in steady-state or state of equilibrium. In this situation, all row vectors are equal. If the original matrix is an
n by
n matrix, we get n vectors that are all the same. We call this vector a fixed probability vector or the equilibrium vector E. In the above problem, the fixed probability vector
E is
. Furthermore, if the equilibrium vector
E is multiplied by the original matrix
T, the result is the equilibrium vector
E. That is,
or,
At the end of the section called “Markov Chains”, we took the transition matrix
T and started taking higher and higher powers of it. The matrix started to stabilize, and finally it reached its steady-state or state of equilibrium. When that happened, all the row vectors became the same, and we called one such row vector a fixed probability vector or an equilibrium vector E. Furthermore, we discovered that
.
In this section, we wish to answer the following four questions.
Does every Markov chain reach a state of equilibrium?
Does the product of an equilibrium vector and its transition matrix always equal the equilibrium vector? That is, does
?
Can the equilibrium vector E be found without raising the matrix to higher powers?
Does the long term market share distribution for a Markov chain depend on the initial market share?
Does every Markov chain reach the state of equilibrium?
Determine whether the following Markov chains are regular.
The matrix A is not a regular Markov chain because every power of it has an entry 0 in the first row, second column position. In fact, we will show that all 2 by 2 matrices that have a zero in the first row, second column position are not regular. Consider the following matrix M.
Observe that the first row, second column entry, a⋅0+0⋅c, will always be zero, regardless of what power we raise the matrix to.
The transition matrix B is a regular Markov chain because
has only positive entries.
Does the product of an equilibrium vector and its transition matrix always equal the equilibrium vector? That is, does
?
At this point, the reader may have already guessed that the answer is yes if the transition matrix is a regular Markov chain. We try to illustrate with the following example from the section called “Markov Chains”.
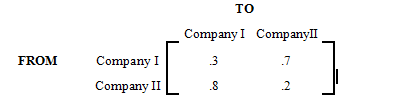
A small town is served by two telephone companies, Mama Bell and Papa Bell. Due to their aggressive sales tactics, each month 40% of Mama Bell customers switch to Papa Bell, that is, the other 60% stay with Mama Bell. On the other hand, 30% of the Papa Bell customers switch to Mama Bell. The transition matrix is given below.
If the initial market share for Mama Bell is 20% and for Papa Bell 80%, we'd like to know the long term market share for each company.
Let matrix T denote the transition matrix for this Markov chain, and M denote the matrix that represents the initial market share. Then T and M are as follows:
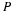and
Since each month the towns people switch according to the transition matrix T, after one month the distribution for each company is as follows:
After two months, the market share for each company is
After three months the distribution is
After four months the market share is
After 30 months the market share is
.
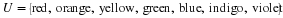The market share after 30 months has stabilized to
.
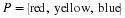This means that
Once the market share reaches an equilibrium state, it stays the same, that is,
.
This helps us answer the next question.
Can the equilibrium vector E be found without raising the transition matrix to large powers?
The answer to the second question provides us with a way to find the equilibrium vector E.
The answer lies in the fact that