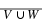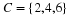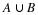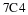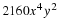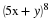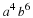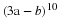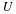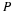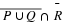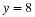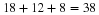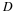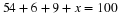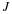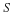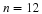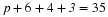In this chapter, you will learn to:
Do matrix operations.
Solve linear systems using the Gauss-Jordan method.
Solve linear systems using the matrix inverse method.
Do application problems.
In this section you will learn to:
Add and subtract matrices.
Multiply a matrix by a scalar.
Multiply two matrices.
A matrix is a rectangular array of numbers. Matrices are useful in organizing and manipulating large amounts of data. In order to get some idea of what matrices are all about, we will look at the following example.
Fine Furniture Company makes chairs and tables at its San Jose, Hayward, and Oakland factories. The total production, in hundreds, from the three factories for the years 1994 and 1995 is listed in the table below.
| ||||||||||||
| San Jose | 30 | 18 | 36 | 20 | ||||||||
| Hayward | 20 | 12 | 24 | 18 | ||||||||
| Oakland | 16 | 10 | 20 | 12 | ||||||||
Represent the production for the years 1994 and 1995 as the matrices A and B.
Find the difference in sales between the years 1994 and 1995.
The company predicts that in the year 2000 the production at these factories will double that of the year 1994. What will the production be for the year 2000?
The matrices are as follows:
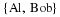
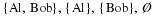
We are looking for the matrix B−A. When two matrices have the same number of rows and columns, the matrices can be added or subtracted entry by entry. Therefore, we get
We would like a matrix that is twice the matrix of 1994, i.e., 2A.
Whenever a matrix is multiplied by a number, each entry is multiplied by the number.
Before we go any further, we need to familiarize ourselves with some terms that are associated with matrices. The numbers in a matrix are called the entries or the elements of a matrix. Whenever we talk about a matrix, we need to know the size or the dimension of the matrix. The dimension of a matrix is the number of rows and columns it has. When we say a matrix is a 3 by 4 matrix, we are saying that it has 3 rows and 4 columns. The rows are always mentioned first and the columns second. This means that a 3×4 matrix does not have the same dimension as a 4×3 matrix. A matrix that has the same number of rows as columns is called a square matrix. A matrix with all entries zero is called a zero matrix. A square matrix with 1's along the main diagonal and zeros everywhere else, is called an identity matrix. When a square matrix is multiplied by an identity matrix of same size, the matrix remains the same. A matrix with only one row is called a row matrix or a row vector, and a matrix with only one column is called a column matrix or a column vector. Two matrices are equal if they have the same size and the corresponding entries are equal.
Matrix Addition and Subtraction
If two matrices have the same size, they can be added or subtracted. The operations are performed on corresponding entries.
Given the matrices A, B, C and D, below
Find, if possible.
A+B
C−D
A+D.
As we mentioned earlier, matrix addition and subtraction involves performing these operations entry by entry.
We add each element of A to the corresponding entry of B.
Just like the problem above, we perform the subtraction entry by entry.
The sum A+D cannot be found because the two matrices have different sizes.
Two matrices can only be added or subtracted if they have the same dimension.
Multiplying a Matrix by a Scalar
If a matrix is multiplied by a scalar (a constant number), each entry is multiplied by that scalar.
Given the matrix A and C in Example 3.2, find 2A and −3C.
To find 2A, we multiply each entry of matrix A by 2, and to find −3C, we multiply each entry of C by −3. The results are given below.
We multiply each entry of A by 2.
We multiply each entry of C by −3.
Multiplication of Two Matrices
To multiply a matrix by another is not as easy as the addition, subtraction, or scalar multiplication of matrices. Because of its wide use in application problems, it is important that we learn it well. Therefore, we will try to learn the process in a step by step manner. We first begin by finding a product of a row matrix and a column matrix.
Given
and
, find the product
.
The product is a 1×1 matrix whose entry is obtained by multiplying the corresponding entries and then forming the sum.
Note that
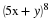is a
1×1 matrix, and its only entry is
2a+3b+4c.
Given
and
, find the product
.
Again, we multiply the corresponding entries and add.
In order for a product of a row matrix and a column matrix to exist, the number of entries in the row matrix must be the same as the number of entries in the column matrix.
Given
and
, find the product
.
We already know how to multiply a row matrix by a column matrix. To find the product
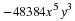, in this example, we will be multiplying the row matrix
A to both the first and second columns of matrix
B, resulting in a
1×2 matrix.
We have just multiplied a 1×3 matrix by a matrix whose size is 3×2. So unlike addition and subtraction, it is possible to multiply two matrices with different dimensions as long as the number of entries in the rows of the first matrix are the same as the number of entries in columns of the second matrix.
Given
and
, find the product
.
This time we are multiplying two rows of the matrix A with two columns of the matrix B. Since the number of entries in each row of A are the same as the number of entries in each column of B, the product is possible. We do exactly what we did in Example 3.6. The only difference is that the matrix A has one more row.
We multiply the first row of the matrix A with the two columns of B, one at a time, and then repeat the process with the second row of A. We get
Given the matrices E, F, G and H, below
Find, if possible.
To find
, we multiply the first row
of
E with the columns
and
of the matrix
F, and then repeat the process by multiplying the other two rows of
E with these columns of
F. The result is as follows:
The product
is not possible because the matrix
F has two entries in each row, while the matrix
E has three entries in each column. In other words, the matrix
F has two columns, while the matrix
E has three rows.
We summarize matrix multiplication as follows:
In order for product
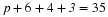to exist, the number of columns of
A, must equal the number of rows of
B. If matrix