In this chapter, you will learn to:
Solve linear programming problems that maximize the objective function.
Solve linear programming problems that minimize the objective function.
Application problems in business, economics, and social and life sciences often ask us to make decisions on the basis of certain conditions. These conditions or constraints often take the form of inequalities. In this section, we will look at such problems.
A typical linear programming problem consists of finding an extreme value of a linear function subject to certain constraints. We are either trying to maximize or minimize our function. That is why these linear programming problems are classified as maximization or minimization problems, or just optimization problems. The function we are trying to optimize is called an objective function, and the conditions that must be satisfied are called constraints. In this chapter, we will do problems that involve only two variables, and therefore, can be solved by graphing. We begin by solving a maximization problem.
Niki holds two part-time jobs, Job I and Job II. She never wants to work more than a total of 12 hours a week. She has determined that for every hour she works at Job I, she needs 2 hours of preparation time, and for every hour she works at Job II, she needs one hour of preparation time, and she cannot spend more than 16 hours for preparation. If she makes $40 an hour at Job I, and $30 an hour at Job II, how many hours should she work per week at each job to maximize her income?
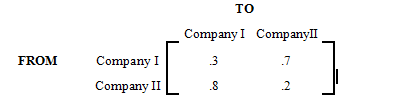
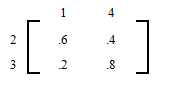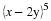We start by choosing our variables.
Let x=The number of hours per week Niki will work at Job I.
and y=The number of hours per week Niki will work at Job II.
Now we write the objective function. Since Niki gets paid $40 an hour at Job I, and $30 an hour at Job II, her total income I is given by the following equation.
Our next task is to find the constraints. The second sentence in the problem states, "She never wants to work more than a total of 12 hours a week." This translates into the following constraint:
The third sentence states, "For every hour she works at Job I, she needs 2 hours of preparation time, and for every hour she works at Job II, she needs one hour of preparation time, and she cannot spend more than 16 hours for preparation." The translation follows.
The fact that x and y can never be negative is represented by the following two constraints:
x≥0, and y≥0.
Well, good news! We have formulated the problem. We restate it as
Maximize I = 40 x + 30 y
Subject to: x + y ≤ 12
In order to solve the problem, we graph the constraints as follows.
Observe that we have shaded the region where all conditions are satisfied. This region is called the feasibility region or the feasibility polygon.
The Fundamental Theorem of Linear Programming states that the maximum (or minimum) value of the objective function always takes place at the vertices of the feasibility region.
Therefore, we will identify all the vertices of the feasibility region. We call these points critical points. They are listed as (0, 0), (0, 12), (4, 8), (8, 0). To maximize Niki's income, we will substitute these points in the objective function to see which point gives us the highest income per week. We list the results below.
| Critical Points | Income |
| (0,0) | 40 ( 0 ) + 30 ( 0 ) = $ 0 |
| (0.12) | 40 ( 0 ) + 30 ( 12 ) = $ 360 |
| (4,8) | 40 ( 4 ) + 30 ( 8 ) = $ 400 |
| (8,0) | 40 ( 8 ) + 30 ( 0 ) = $ 320 |
Clearly, the point (4, 8) gives the most profit: $400.
Therefore, we conclude that Niki should work 4 hours at Job I, and 8 hours at Job II.
A factory manufactures two types of gadgets, regular and premium. Each gadget requires the use of two operations, assembly and finishing, and there are at most 12 hours available for each operation. A regular gadget requires 1 hour of assembly and 2 hours of finishing, while a premium gadget needs 2 hours of assembly and 1 hour of finishing. Due to other restrictions, the company can make at most 7 gadgets a day. If a profit of $20 is realized for each regular gadget and $30 for a premium gadget, how many of each should be manufactured to maximize profit?
We choose our variables.
Let x=The number of regular gadgets manufactured each day.
and y=The number of premium gadgets manufactured each day.
The objective function is
We now write the constraints. The fourth sentence states that the company can make at most 7 gadgets a day. This translates as
Since the regular gadget requires one hour of assembly and the premium gadget requires two hours of assembly, and there are at most 12 hours available for this operation, we get
Similarly, the regular gadget requires two hours of finishing and the premium gadget one hour. Again, there are at most 12 hours available for finishing. This gives us the following constraint.
The fact that x and y can never be negative is represented by the following two constraints:
x≥0, and y≥0.
We have formulated the problem as follows:
Maximize P = 20 x + 30 y
Subject to: x + y ≤ 7
In order to solve the problem, we graph the constraints as follows:
Again, we have shaded the feasibility region, where all constraints are satisfied.
Since the extreme value of the objective function always takes place at the vertices of the feasibility region, we identify all the critical points. They are listed as (0, 0), (0, 6), (2, 5), (5, 2), and (6, 0). To maximize profit, we will substitute these points in the objective function to see which point gives us the maximum profit each day. The results are listed below.
| Critical point | Income |
| (0,0) | 20 ( 0 ) + 30 ( 0 ) = $ 0 |
| (0,6) | 20 ( 0 ) + 30 ( 6 ) = $ 180 |
| (2,5) | 20 ( 2 ) + 30 ( 5 ) = $ 190 |
| (5,2) | 20 ( 5 ) + 30 ( 2 ) = $ 160 |
| (6,0) | 20 ( 6 ) + 30 ( 0 ) = $ 120 |
The point (2, 5) gives the most profit, and that profit is $190. Therefore, we conclude that we should manufacture 2 regular gadgets and 5 premium gadgets daily for a profit of $190.
Although we are mostly focusing on the standard maximization problems where all constraints are of the form
, we will now consider an example where that is not the case.
Solve the following maximization problem graphically.
Maximize P = 10 x + 15 y
Subject to: x + y ≥ 1
The graph is shown below.
The five critical points are listed in the above figure. Clearly, the point (2, 2) maximizes the objective function to a maximum value of 50. The reader should observe that the first constraint x+y≥1 requires that feasibility region must be bounded below by the line x+y=1.
Finally, we address an important question. Is it possible to determine the point that gives the maximum value without calculating the value at each critical point?
The answer is yes.
For example, in the above problem, we substituted the points (0, 0), (0, 6), (2, 5), (5, 2), and (6, 0), in the objective function P=20x+30y