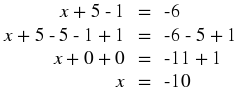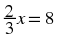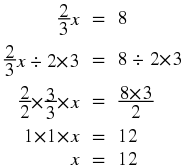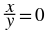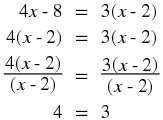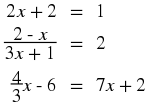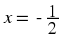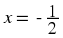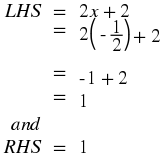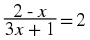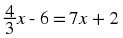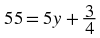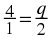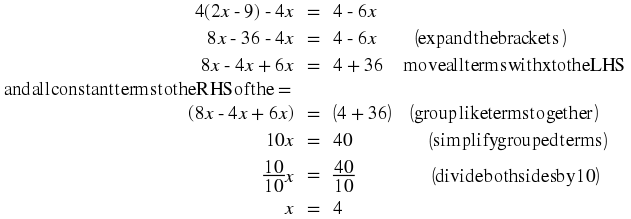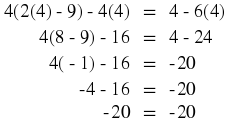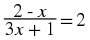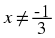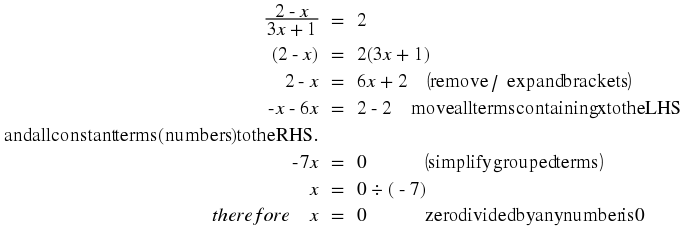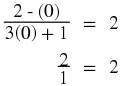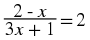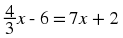This chapter is all about solving different types of equations for one or two variables. In general, we want to get the unknown variable alone on the left hand side of the equation with all the constants on the right hand side of the equation. For example, in the equation x – 1 = 0, we want to be able to write the equation as x = 1.
As we saw in review of past work (section on rearranging equations), an equation is like a set of weighing scales that must always be balanced. When we solve equations, we need to keep in mind that what is done to one side must be done to the other.
You can add, subtract, multiply or divide both sides of an equation by any number you want, as long as you always do it to both sides.
For example, in the equation x + 5 – 1 = – 6, we want to get x alone on the left hand side of the equation. This means we need to subtract 5 and add 1 on the left hand side. However, because we need to keep the equation balanced, we also need to subtract 5 and add 1 on the right hand side.
In another example,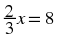 
, we must divide by 2 and multiply by 3 on the left hand side in order to get
x
alone. However, in order to keep the equation balanced, we must also divide by 2 and multiply by 3 on the right hand side.
These are the basic rules to apply when simplifying any equation. In most cases, these rules have to be applied more than once, before we have the unknown variable on the left hand side of the equation.
The following must also be kept in mind:
Division by 0 is undefined.
If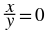 
, then
x = 0 and
y ≠ 0, because division by 0 is
undefined.
We are now ready to solve some equations!
In the following, identify what is wrong.
The simplest equation to solve is a linear equation. A linear equation is an equation where the power of the variable(letter, e.g. x ) is 1(one). The following are examples of linear equations.
In this section, we will learn how to find the value of the variable that makes both sides of the linear equation true. For example, what value of x makes both sides of the very simple equation, x + 1 = 1 true.
Since the definition of a linear equation is that if the variable has a highest power of one (1), there is at most one solution or root for the equation.
This section relies on all the methods we have already discussed: multiplying out expressions, grouping terms and factorisation. Make sure that you are comfortable with these methods, before trying out the work in the rest of this chapter.
Now we see that 2x = – 1. This means if we divide both sides by 2, we will get:
If we substitute 
, back into the original equation, we get:
That is all that there is to solving linear equations.
Solving Equations
When you have found the solution to an equation, substitute the solution into the original equation, to check your answer.
The general steps to solve equations are:
Expand (Remove) all brackets.
"Move" all terms with the variable to the left hand side of the equation, and all constant terms (the numbers) to the right hand side of the equals sign. Bearing in mind that the sign of the terms will change from ( + ) to ( – ) or vice versa, as they "cross over" the equals sign.
Group all like terms together and simplify as much as possible.
Factorise if necessary.
Find the solution.
Substitute solution into original equation to check answer.
Figure 4.1. Khan academy video on equations - 1
Solve for y : 2y – 3 = 7 Click here for the solution
Solve for w : – 3w = 0 Click here for the solution
Solve for z : 4z = 16 Click here for the solution
Solve for t : 12t + 0 = 144 Click here for the solution
Solve for x : 7 + 5x = 62 Click here for the solution
Solve for
y
: 
Click here for the solution
Solve for z : 5z = 3z + 45 Click here for the solution
Solve for a : 23a – 12 = 6 + 2a Click here for the solution
Solve for b : 12 – 6b + 34b = 2b – 24 – 64 Click here for the solution
Solve for c : 6c + 3c = 4 – 5(2c – 3) Click here for the solution
Solve for p : 18 – 2p = p + 9 Click here for the solution
Solve for
q
: 
Click here for the solution
Solve for
q
: 
Click here for the solution
Solve for r : – ( – 16 – r) = 13r – 1 Click here for the solution
Solve for d : 6d – 2 + 2d = – 2 + 4d + 8 Click here for the solution
Solve for f : 3f – 10 = 10 Click here for the solution
Solve for v : 3v + 16 = 4v – 10 Click here for the solution
Solve for k : 10k + 5 + 0 = – 2k + – 3k + 80 Click here for the solution
Solve for j : 8(j – 4) = 5(j – 4) Click here for the solution
Solve for m : 6 = 6(m + 7) + 5m Click here for the solution
Solution to Exercise 4.1.1. (Return to Exercise)
We are given 4 – x = 4 and are required to solve for x .
Since there are no brackets, we can start with grouping like terms and then simplifying.
Solve the problem :
Substitute solution into original equation:
Since both sides are equal, the answer is correct.
The solution of 4 – x = 4 is x = 0.
Solution to Exercise 4.1.2. (Return to Exercise)
We are given 4(2x – 9) – 4x = 4 – 6x and are required to solve for x .
We start with expanding the brackets, then grouping like terms and then simplifying.
Solve the problem :
Substitute solution into original equation:
Since both sides are equal to – 20, the answer is correct.
The solution of 4(2x – 9) – 4x = 4 – 6x is x = 4.
Solution to Exercise 4.1.3. (Return to Exercise)
We are given 
and are required to solve for
x
.
Since there is a denominator of (
3
x + 1
), we can start by multiplying both sides
of the equation by (
3
x + 1
). But because division by 0 is not permissible, there
is a restriction on a value for x. (
)
Solve the problem :
Substitute solution into original equation:
Since both sides are equal to 2, the answer is correct.
The solution of 
is
x = 0.
Solution to Exercise 4.1.4. (Return to Exercise)
We are given 
and are required to solve for
x
.
We start with multiplying each of the terms in the equation by 3, then grouping like terms and then simplifying.
Solve the problem :
