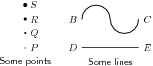
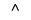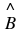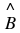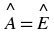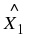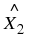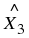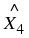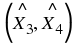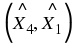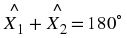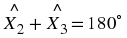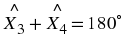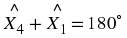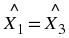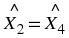The two simplest objects in geometry are points and lines.
A point is a coordinate that marks a position in space (on a number line, on a plane or in three dimensions or even more) and is denoted by a dot. Points are usually labelled with a capital letter. Some examples of how points can be represented are shown in Figure 7.1.
A line is a continuous set of coordinates in space and can be thought of as being formed when many points are placed next to each other. Lines can be straight or curved, but are always continuous. This means that there are never any breaks in the lines. The endpoints of lines are labelled with capital letters. Examples of two lines are shown in Figure 7.1.
Lines are labelled according to the start point and end point. We call the line that starts at a point
A
and ends at a point
B
,
A
B
. Since the line from point
B
to point
A
is the same as the line from point
A
to point
B
, we have that
A
B = B
A
.
The length of the line between points
A
and
B
is
A
B
. So if we say
A
B = C
D
we mean that the length of the line between
A
and
B
is equal to the length of the line between
C
and
D
.
A line is measured in units of length. Some common units of length are listed in Table 7.1.
Table 7.1. Some common units of length and their abbreviations.|
Unit of Length
|
Abbreviation
|
| kilometre | km |
| metre | m |
| centimetre | cm |
| millimetre | mm |
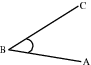
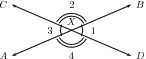
An angle is formed when two straight lines meet at a point. The point at which two lines meet is known as a vertex. Angles are labelled with a 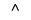 called a caret on a letter. For example, in Figure 7.2 the angle is at
called a caret on a letter. For example, in Figure 7.2 the angle is at 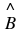 . Angles can also be labelled according to the line segments that make up the angle. For example, in Figure 7.2 the angle is made up when line segments
C
B
and
B
A
meet. So, the angle can be referred to as
∠CBA
or
∠ABC
. The
∠
symbol is a short method of writing angle in geometry.
. Angles can also be labelled according to the line segments that make up the angle. For example, in Figure 7.2 the angle is made up when line segments
C
B
and
B
A
meet. So, the angle can be referred to as
∠CBA
or
∠ABC
. The
∠
symbol is a short method of writing angle in geometry.
Angles are measured in degrees which is denoted by
∘ , a small circle raised above the text in the same fashion as an exponent (or a superscript).
Note
Angles can also be measured in radians. At high school level you will only use degrees, but if you decide to take maths at university you will learn about radians.
The size of an angle does not depend on the length of the lines that are joined to make up the angle, but depends only on how both the lines are placed as can be seen in Figure 7.3. This means that the idea of length cannot be used to measure angles. An angle is a rotation around the vertex.
A protractor is a simple tool that is used to measure angles. A picture of a protractor is shown in Figure 7.4.
Method:
Using a protractor
Place the bottom line of the protractor along one line of the angle so that the other line of the angle points at the degree markings.
Move the protractor along the line so that the centre point on the protractor is at the vertex of the two lines that make up the angle.
Follow the second line until it meets the marking on the protractor and read off the angle. Make sure you start measuring at 0
∘ .
Measuring Angles : Use a protractor to measure the following angles:
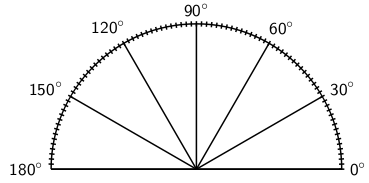
What is the smallest angle that can be drawn? The figure below shows two lines (
CA
and
AB
) making an angle at a common vertex
A
. If line
CA
is rotated around the common vertex
A
, down towards line
AB
, then the smallest angle that can be drawn occurs when the two lines are pointing in the same direction. This gives an angle of 0
∘ . This is shown in Figure 7.6
If line
CA
is now swung upwards, any other angle can be obtained. If line
CA
and line
AB
point in opposite directions (the third case in Figure 7.6) then this forms an angle of 180
∘ .
Note
If three points
A
,
B
and
C
lie on a straight line, then the angle between them is 180
∘ . Conversely, if the angle between three points is 180
∘ , then the points lie on a straight line.
An angle of 90
∘ is called a right angle. A right angle is half the size of the angle made by a straight line (180
∘ ). We say
CA
is perpendicular to
AB
or
C
A ⊥ A
B
. An angle twice the size of a straight line is 360
∘ . An angle measuring 360
∘ looks identical to an angle of 0
∘ , except for the labelling. We call this a revolution.
All angles larger than 360
∘ also look like we have seen them before. If you are given an angle that is larger than 360
∘ , continue subtracting 360
∘ from the angle, until you get an answer that is between 0
∘ and 360
∘ . Angles that measure more than 360
∘ are largely for mathematical convenience.
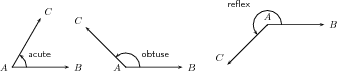
Note
Acute angle: An angle ≥ 0 ∘ and < 90 ∘ .
Right angle: An angle measuring 90 ∘ .
Obtuse angle: An angle > 90 ∘ and < 180 ∘ .
Straight angle: An angle measuring 180
∘ .
Reflex angle: An angle > 180 ∘ and < 360 ∘ .
Revolution: An angle measuring 360 ∘ .
These are simply labels for angles in particular ranges, shown in Figure 7.8.
Once angles can be measured, they can then be compared. For example, all right angles are 90
∘ , therefore all right angles are equal and an obtuse angle will always be larger than an acute angle.
The following video summarizes what you have learnt so far about angles.
Note that for high school trigonometry you will be using degrees, not radians as stated in the video. Radians are simply another way to measure angles. At university level you will learn about radians.
Parallel Lines intersected by Transversal Lines
Two lines intersect if they cross each other at a point. For example, at a traffic intersection two or more streets intersect; the middle of the intersection is the common point between the streets.
Parallel lines are lines that never intersect. For example the tracks of a railway line are parallel. We wouldn't want the tracks to intersect as