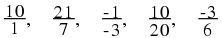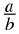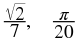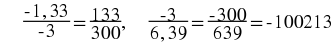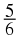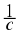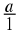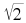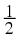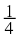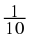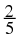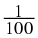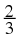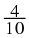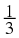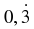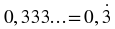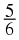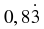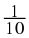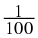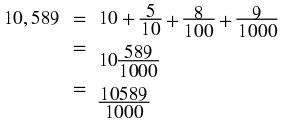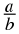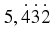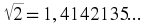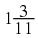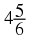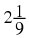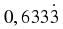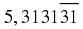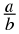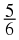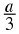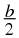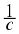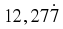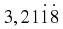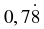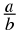As described in the chapter on review of past work, a number is a way of representing quantity. The numbers that will be used in high school are all real numbers, but there are many different ways of writing any single real number.
This chapter describes rational numbers.
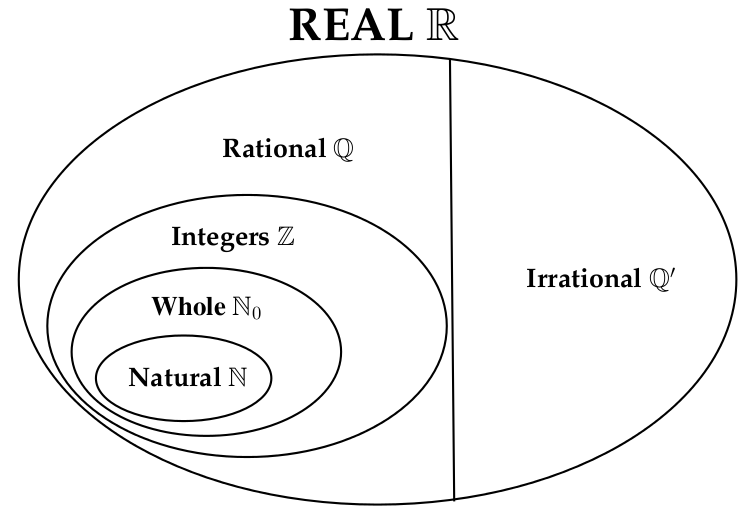
2. The Big Picture of Numbers
The term whole number does not have a consistent definition. Various authors use
it in many different ways. We use the following definitions:
natural numbers are (1, 2, 3, ...)
whole numbers are (0, 1, 2, 3, ...)
integers are (... -3, -2, -1, 0, 1, 2, 3, ....)
The following numbers are all rational numbers.
You can see that all denominators and all numerators are integers.
- Definition: Rational Number
A rational number is any number which can be written as:
where
a
and
b
are integers and
b ≠ 0.
Note
Only fractions which have a numerator and a denominator (that is not 0) that are integers
are rational numbers.
This means that all integers are rational numbers, because they can be written with a denominator of 1.
Therefore
are not examples of rational numbers, because in each case, either the numerator or the denominator is not an integer.
A number may not be written as an integer divided by another integer, but may still
be a rational number. This is because the results may be expressed
as an integer divided by an integer. The rule is, if a number can be written
as a fraction of integers, it is rational even if it can also be written in another
way as well. Here are two examples that might not look like rational numbers
at first glance but are because there are equivalent forms that are expressed as an
integer divided by another integer:
If
a
is an integer,
b
is an integer and
c
is irrational, which of the following are rational numbers?
Table 1. (i) 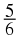
| (ii) 
| (iii) 
| (iv) 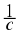
|
Click here for the solution
If 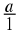 is a rational number, which of the following are valid values for
a
?
is a rational number, which of the following are valid values for
a
?
Table 2. | (i) 1 | (ii) – 10
| (iii) 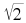
| (iv) 2,1
|
Click here for the solution
4. Forms of Rational Numbers
All integers and fractions with integer numerators and denominators are rational numbers. There are two more forms of rational numbers.
Investigation : Decimal Numbers
You can write the rational number
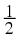 as the decimal number 0,5. Write the following numbers as
decimals:
as the decimal number 0,5. Write the following numbers as
decimals:
Do the numbers after the decimal comma end or do they continue? If they continue, is there a repeating pattern to the numbers?
You can write a rational number as a decimal number. Two types of decimal numbers can be written as rational numbers:
For example, the rational number 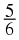 can be written in decimal notation as
can be written in decimal notation as 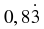 and similarly, the decimal number 0,25 can be written as a rational number as
and similarly, the decimal number 0,25 can be written as a rational number as  .
.
Notation for Repeating Decimals
You can use a bar over the repeated numbers to indicate that the decimal is a repeating decimal.
5. Converting Terminating Decimals into Rational Numbers
A decimal number has an integer part and a fractional part. For example 10,589 has an integer part of 10 and a fractional part of 0,589 because 10 + 0,589 = 10,589. The fractional part can be written as a rational number, i.e. with a numerator and a denominator that are integers.
Each digit after the decimal point is a fraction with a denominator in increasing powers of ten. For example:
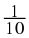 is 0,1
is 0,1
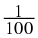 is 0,01
is 0,01
This means that:
6. Converting Repeating Decimals into Rational Numbers
When the decimal is a repeating decimal, a bit more work is needed to write the fractional part of the decimal number as a fraction. We will explain by means of an example.
If we wish to write  in the form
in the form 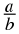 (where
a
and
b
are integers) then we would proceed as follows
(where
a
and
b
are integers) then we would proceed as follows
And another example would be to write
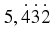 as a rational fraction.
as a rational fraction.
For the first example, the decimal was multiplied by 10 and for the second example, the decimal was multiplied by 1000. This is because for the first example there was only one digit (i.e. 3) recurring, while for the second example there were three digits (i.e. 432) recurring.
In general, if you have one digit recurring, then multiply by 10. If you have two digits recurring, then multiply by 100. If you have three digits recurring, then multiply by 1000. Can you spot the pattern yet?
The number of zeros is the same as the number of recurring digits.
Not all decimal numbers can be written as rational numbers. Why? Irrational decimal numbers like
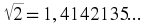 cannot be written with an integer numerator and denominator, because they do not have a pattern of recurring digits. However, when possible, you should try to use rational numbers or fractions instead of decimals.
cannot be written with an integer numerator and denominator, because they do not have a pattern of recurring digits. However, when possible, you should try to use rational numbers or fractions instead of decimals.
Repeated Decimal Notation
Real numbers can be either rational or irrational.
A rational number is any number which can be written as
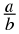 where
a
and
b
are integers and
b ≠ 0
where
a
and
b
are integers and
b ≠ 0
The following are rational numbers:
Fractions with both denominator and numerator as integers.
Integers.
Decimal numbers that end.
Decimal numbers that repeat.
8. End of Chapter Exercises