Chapter 1. The Real and Complex Numbers
1.1. Definition of the Numbers 1, i, and the square root of 2*
In order to make precise sense out of the concepts we study in mathematical analysis, we must first come to terms with what the "real numbers" are. Everything in mathematical analysis is based on these numbers, and their very definition and existence is quite deep. We will, in fact, not attempt to demonstrate (prove) the existence of the real numbers in the body of this text, but will content ourselves with a careful delineation of their properties, referring the interested reader to an appendix for the existence and uniqueness proofs.
Although people may always have had an intuitive idea of what these
real numbers were, it was not until the nineteenth century that mathematically precise definitions were given. The history of how mathematicians came to realize the necessity for such precision in their definitions is fascinating from a philosophical point of view as much as from a mathematical one. However, we will not pursue the philosophical aspects of the subject in this book, but will be content to concentrate our attention just on the mathematical facts. These precise definitions are quite complicated, but the powerful possibilities within mathematical analysis rely heavily on this precision, so we must pursue them. Toward our primary goals, we will in this chapter give definitions of the symbols (numbers) 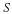 and
and 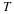
The main points of this chapter are the following:
The notions of least upper bound (supremum) and greatest lower bound
(infimum) of a set of numbers,
The definition of the real numbersR,
the formula for the sum of a geometric progression (Theorem 1.9.),
the Binomial Theorem (Theorem 1.10.), and
the triangle inequality for complex numbers (Theorem 1.15.).
1.2. The Natural Numbers and the Integers*
We will take for granted that we understand the existence of what we call the natural numbers, i.e., the set N whose elements are the numbers 1,2,3,4,.... Indeed, the two salient properties of this set are that (a) there is a frist element (the natural number 1), and (b) for each element n of this set there is a “very next” one, i.e., an immediate successor. We assume that the algebraic notions of sum and product of natural numbers is well-defined and familiar. These operations satisfy three basic relations:
Basic Algebraic Relations.
(Commutativity) n+m=m+n and n×m=m×n for all n,m∈N.
(Associativity) n+(m+k)=(n+m)+k and n×(m×k)=(n×m)×k
for all n,m,k∈N.
(Distributivity) n×(m+k)=n×m+n×k
for all n,m,k∈N.
We also take as given the notion of one natural number being larger than another one.
2>1,5>3,n+1>n, etc.
We will accept as true the axiom of mathematical induction, that is, the following statement:
AXIOM OF MATHEMATICAL INDUCTION.
Let S be a subset of the set N of natural numbers. Suppose that
1∈S.
If a natural number k is in S, then the natural number k+1 also is in S.
Then S=N.
That is, every natural number n belongs to S.
REMARK The axiom of mathematical induction is for our purposes frequently employed as a
method of proof. That is, if we wish to show that a certain proposition holds for all
natural numbers, then we let S denote the set of numbers
for which the proposition is true, and then, using the axiom
of mathematical induction, we verify that S is all of N
by showing that S satisfies both of the above conditions. Mathematical induction can also be used as a method of definition. That is, using it, we can define an infinite number of objects 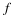 that are indexed by the natural numbers. Think of S as the set of natural numbers for which the object On is defined. We check first to see that the object O1 is defined. We check next that, if the object Ok is defined for a natural number k, then there is a prescribed procedure for defining the object Ok+1. So, by the axiom of mathematical induction, the object is defined for all natural numbers. This method of defining an infinite set of objects is often referred to as sl recursive definition, or definition by recursion.
that are indexed by the natural numbers. Think of S as the set of natural numbers for which the object On is defined. We check first to see that the object O1 is defined. We check next that, if the object Ok is defined for a natural number k, then there is a prescribed procedure for defining the object Ok+1. So, by the axiom of mathematical induction, the object is defined for all natural numbers. This method of defining an infinite set of objects is often referred to as sl recursive definition, or definition by recursion.
As an example of recursive definition, let us carefully define exponentiation.
- Definition:
Let a be a natural number. We define inductively natural numbers an as follows: a1=a, and, whenever ak is defined, then ak+1 is defined to be a×ak.
The set S of all natural numbers for which an is defined is therefore all of N. For, a1 is defined, and if ak is defined there is a prescription for defining ak+1. This “careful” definition of an may seem unnecessarily detailed. Why not simply define an as a×a×a×a...×an times? The answer is that the ..., though suggestive enough, is just not mathematically precise. After all, how would you explain what ... means? The answer to that is that you invent a recursive definition to make the intuitive meaning of the ... mathematically precise. We will of course use the symbol ... to simplify and shorten our notation, but keep in mind that, if pressed, we should be able to provide a careful definition.
Exercise 1.
Derive the three laws of exponents for the natural numbers:
an+m=an×am.
HINT: Fix a and m and use the axiom of mathematical induction.
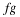 HINT: Fix a and m and use the axiom of mathematical induction.
(a×b)n=an×bn.
HINT: Fix a and b and use the axiom of mathematical induction.
HINT: Fix a and m and use the axiom of mathematical induction.
(a×b)n=an×bn.
HINT: Fix a and b and use the axiom of mathematical induction.
Define inductively numbers 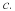 as follows:
S1=1, and if Sk is defined, then Sk+1 is defined to be Sk+k+1.
Prove, by induction, that
Sn=n(n+1)/2.
Note that we could have defined Sn using the ... notation by Sn=1+2+3+...+n.
as follows:
S1=1, and if Sk is defined, then Sk+1 is defined to be Sk+k+1.
Prove, by induction, that
Sn=n(n+1)/2.
Note that we could have defined Sn using the ... notation by Sn=1+2+3+...+n.
Prove that
()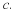
Make a recursive definition of n!=1×2×3×...×n.n! is called n factorial.
There is a slightly more general statement of the axiom of mathematical
induction, which is sometimes of use.
GENERAL AXIOM OF MATHEMATICAL INDUCTION
Let S be a subset of the set N of natural numbers, and suppose that
S satisfies the following conditions
There exists a natural number k0
such that k0∈S.
If S contains a natural number k, then S contains the
natural number k+1.
Then S contains every natural number n that is larger than or equal to k0.
From the fundamental set N of natural numbers, we construct
the set Z of all integers.
First, we simply create an additional number called 0 that satisfies
the equations 0+n=n for all n∈N and
0×n=0 for all n∈N.
The word “create” is, for some mathematicians,
a little unsettling. In fact, the idea of zero did not appear in mathematics
until around the year 900.
It is easy to see how the so-called natural numbers came by their
name. Fingers, toes, trees, fish, etc., can all be counted,
and the very concept of counting is what the natural numbers are about.
On the other hand, one never needed to count zero fingers or fish, so that the notion of zero as a number easily could have
only come into mathematics at a later time, a time when arithmetic was becoming more sophisticated.
In any case, from our twenty-first century viewpoint, 0 seems very understandable,
and we won't belabor the fundamental question of its existence any further here.
Next, we introduce the so-called negative numbers.
This is again quite reasonable from our point of view.
For every natural number n, we let –n be a number which, when added to
n, give 0.
Again, the question of whether or not such negative numbers exist
will not concern us here.
We simply create them.
In short, we will take as given the existence of a
set Z, called the integers,
which comprises the set N
of natural numbers, the additional number 0, and the set –N of all negative numbers.
We assume that addition and multiplication of integers satisfy the three
basic algebraic relations of commutativity, associativity, and distributivity stated above.
We also assume that the following additional relations hold:
for all natural numbers n and k.
1.3. The Rational Numbers*
Next, we discuss the set Q of rational numbers, which we ordinarily think of as quotients k/n of integers. Of course, we do not allow the “second” element n of the quotient k/n to be 0. Also, we must remember that there isn't a 1-1 correspondence between the set Q of all rational numbers and the set of all such quotients k/n. Indeed, the two distinct quotients 2/3 and 6/9 represent the same rational number. To be precise, the set Q is a collection of equivalence classes of ordered pairs (k,n) of integers, for which the second component of the pair is not 0. The equivalence relation among these ordered pairs is this:
We will not dwell on this possibly subtle definition, but will rather accept the usual understanding of the rational numbers and their arithmetic properties. In particular, we will represent them as quotients rather than as ordered pairs, and, if r is a rational number, we will write r=k/n, instead of writing r as the equivalence class containing the ordered pair (k,n). As usual, we refer to the first integer in the quotient k/n as the numerator and the second (nonzero) integer in the quotient k/n as the denominator of the quotient. The familiar definitions of sum and product for rational numbers are these:
and
Addition and multiplication of rational numbers satisfy the three basic algebraic relations of commutativity, associativity and distributivity stated earlier.
We note that the integers Z can be identified in an obvious way as a subset of the rational numbers Q. Indeed, we identify the
integer k with the quotient k/1. In this way, we note that Q contains the two numbers 0≡0/1 and 1≡1/1. Notice that any other quotient k/n that is equivalent to 0/1 must satisfy k=0, and any other quotient k/n that is equivalent to 1/1 must satisfy k=n.
Remember, k/n≡k'/n' if and only if kn'=k'n.
The set Q has an additional property not shared by the set of integers Z. It is this: For each nonzero element r∈Q, there exists an element r'∈Q for which r×r'