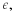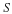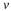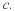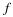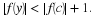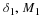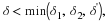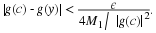In this chapter we will finally see why eiπ is –1. Along the way, we will give careful proofs of all the standard theorems of Differential Calculus, and in the process we will discover all the familiar facts about the trigonometric and exponential functions. At this point, we only know their definitions as power series functions. The fact that sin2+cos2=1 or that ex+y=exey are not at all obvious. In fact, we haven't even yet defined what is meant by ex for an arbitrary number x.
The main theorems of this chapter include:
The Chain Rule (Theorem 4.7.),
The Mean Value Theorem (Theorem 4.9.),
The Inverse Function Theorem (Theorem 4.10.),
The Laws of Exponents (m36173 and Corollary 4.1.), and
Taylor's Remainder Theorem (Theorem 4.19.).
The concept of the derivative of a function is what most people think of as the beginning of calculus. However, before we can even define the derivative we must introduce a kind of generalization of the notion of continuity. That is, we must begin with the definition of the limit of a function.
Let f:S→C be a function, where S⊆C, and let c be a limit point of S that is not necessarily an element of S. We say that fhas a limit L as z approaches c, and we write
if for every ϵ>0 there exists a δ>0 such that if z∈S and 0<|z–c|<δ, then |f(z)–L|<ϵ.
If the domain S is unbounded, we say that f has a limit L as z approaches∞, and we write
if for every ϵ>0 there exists a positive number B such that if z∈S and |z|≥B, then |f(z)–L|<ϵ.
Analogously, if S⊆R, we say limx→∞f(x)=L if for every ϵ>0 there exists a real number B such that if x∈S and x≥B, then |f(x)–L|<ϵ. And we say that limx→–∞f(x)=L if for every ϵ>0 there exists a real number B such that if x∈S and x≤B, then |f(x)–L|<ϵ.
Finally, for f:(a,b)→C a function of a real variable, and for c∈[a,b], we define the one-sided (left and right) limits of f at c. We say that f has a left hand limit of L at c, and we write L=limx→c–0f(x), if for every ϵ>0 there exists a δ>0 such that if x∈(a,b) and 0<c–x<δ then |f(x)–L|<ϵ. We say that f has a right hand limit of L at c, and write L=limx→c+0f(x), if for every ϵ>0 there exists a δ>0 such that if x∈S and 0<x–c<δ then |f(x)–L|<ϵ.
The first few results about limits of functions are not surprising. The analogy between functions having limits and functions being continuous is very close, so that for every elementary result about continuous functions there will be a companion result about limits of functions.
Let c be a complex number. Let f:S→C and g:S→C be functions. Assume that both fand g have limits as x approaches c. Then:
There exists a δ>0 and a positive number M such that if z∈S and 0<|z–c|<δ then |f(z)|<M. That is, if f has a limit as z approaches c, then f is bounded near c.
If limz→cg(z)≠0, then
If u and v are the real and imaginary parts of a complex-valued function f, then u and v have limits as z approaches c if and only if f has a limit as z approaches c. And,
Prove Theorem 4.1.. HINT: Compare with Theorem 3.2..
Prove that limx→cf(x)=L if and only if, for every sequence 
of elements of S that converges to c, we have 
HINT: Compare with Theorem 3.4..
Prove the analog of Theorem 4.1. replacing the limit as z approaches c by the limit as z approaches ∞.
Prove that a function f:S→C is continuous at a point c of S if and only if limx→cf(x)=f(c). HINT: Carefully write down both definitions, and observe that they are verbetim the same.
Let f be a function with domain S, and let c be a limit point of S that is not in S. Suppose g is a function with domain S∪{c}, that f(x)=g(x) for all x∈S, and that g is continuous at c. Prove that limx→cf(x)=g(c).
Prove that the following functions f have the specified limits L at the given points c.
and L=3.
and L=1.
and L=–4/3.
and L=–1.
Define f on the set S of all nonzero real numbers by f(x)=c if x<0 and f(x)=d if x>0. Show that limx→0f(x) exists if and only if c=d.
(b) Let f:(a,b)→C be a complex-valued function on the open interval (a,b). Suppose c is a point of (a,b). Prove that limx→cf(x) exists if and only if the two one-sided limits limx→c–0f(x) and limx→c+0f(x) exist and are equal.
Suppose f:S→C is a function, and that limx→cf(x)=L. Define a function g by g(y)=f(y+c).
What is the domain of g?
Show that 0 is a limit point of the domain of g and that limy→0g(y)=limx→cf(x).
Suppose T⊆C, that h:T→S, and that limy→dh(y)=c. Prove that
REMARK When we use the word “ interior” in connection with a set S, it is obviously important to understand the context; i.e., is S being thought of as a set of real numbers or as a set of complex numbers. A point c is in the interior of a set S of complex numbers if the entire disk Bϵ(c) of radius ϵ around