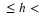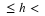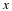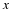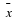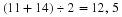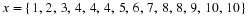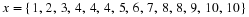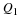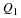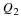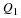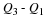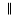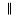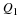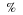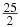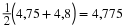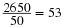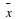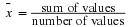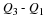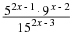You should know by now what the nth root of a number means. If the nth root of a number cannot be simplified to a rational number, we call it a surd. For example,  and
and 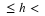 are surds, but
are surds, but  is not a surd because it can be simplified to the rational number 2.
is not a surd because it can be simplified to the rational number 2.
In this chapter we will only look at surds that look like 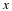 , where a is any positive number, for example
, where a is any positive number, for example 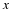 or
or 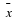 . It is very common for n to be 2, so we usually do not write
. It is very common for n to be 2, so we usually do not write  . Instead we write the surd as just
. Instead we write the surd as just  , which is much easier to read.
, which is much easier to read.
It is sometimes useful to know the approximate value of a surd without having to use a calculator. For example, we want to be able to estimate where a surd like  is on the number line. So how do we know where surds lie on the number line? From a calculator we know that
is on the number line. So how do we know where surds lie on the number line? From a calculator we know that  is equal to 1,73205.... It is easy to see that
is equal to 1,73205.... It is easy to see that  is above 1 and below 2. But to see this for other surds like
is above 1 and below 2. But to see this for other surds like  without using a calculator, you must first understand the following fact:
without using a calculator, you must first understand the following fact:
Interesting Fact
If a and b are positive whole numbers, and a<b, then 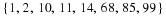 . (Challenge: Can you explain why?)
. (Challenge: Can you explain why?)
If you don't believe this fact, check it for a few numbers to convince yourself it is true.
How do we use this fact to help us guess what 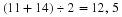 is? Well, you can easily see that 18<25. Using our rule, we also know that
is? Well, you can easily see that 18<25. Using our rule, we also know that  . But we know that 52=25 so that
. But we know that 52=25 so that  . Now it is easy to simplify to get
. Now it is easy to simplify to get  . Now we have a better idea of what
. Now we have a better idea of what  is.
is.
Now we know that  is less than 5, but this is only half the story. We can use the same trick again, but this time with 18 on the right-hand side. You will agree that 16<18. Using our rule again, we also know that
is less than 5, but this is only half the story. We can use the same trick again, but this time with 18 on the right-hand side. You will agree that 16<18. Using our rule again, we also know that 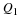 . But we know that 16 is a perfect square, so we can simplify
. But we know that 16 is a perfect square, so we can simplify  to 4, and so we get
to 4, and so we get  !
!
As you can see, we have shown that  is between 4 and 5. If we check on our calculator, we can see that
is between 4 and 5. If we check on our calculator, we can see that 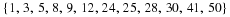 , and the idea was right! You will notice that our idea used perfect squares that were close to the number 18. We found the largest perfect square smaller than 18 was 42=16, and the smallest perfect square greater than 18 was 52=25. Here is a quick summary of what a perfect square or cube is:
, and the idea was right! You will notice that our idea used perfect squares that were close to the number 18. We found the largest perfect square smaller than 18 was 42=16, and the smallest perfect square greater than 18 was 52=25. Here is a quick summary of what a perfect square or cube is:
Interesting Fact
A perfect square is the number obtained when an integer is squared. For example, 9 is a perfect square since 32=9. Similarly, a perfect cube is a number which is the cube of an integer. For example, 27 is a perfect cube, because 33=27.
To make it easier to use our idea, we will create a list of some of the perfect squares and perfect cubes. The list is shown in Table 7.1.
Table 7.1. Some perfect squares and perfect cubes| Integer | Perfect Square | Perfect Cube |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 729 |
| 10 | 100 | 1000 |
When given the surd 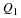 you should be able to tell that it lies somewhere between 3 and 4, because
you should be able to tell that it lies somewhere between 3 and 4, because 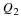 and
and  and 52 is between 27 and 64. In fact
and 52 is between 27 and 64. In fact 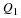 which is indeed between 3 and 4.
which is indeed between 3 and 4.
Find the two consecutive integers such that  lies between them.
lies between them.
(Remember that consecutive numbers are two numbers one after the other, like 5 and 6 or 8 and 9.)
- From the table find the largest perfect square below 26 :
This is 52=25. Therefore 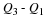 .
.
- From the table find the smallest perfect square above 26 :
This is 62=36. Therefore  .
.
- Put the inequalities together :
Our answer is 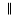 .
.
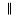 lies between:
lies between:
1 and 2
2 and 3
3 and 4
4 and 5