VERY
ALL
LITTLE
LOT
MUCH
I struggle to subtract quickly and
accurately

I struggle to subtract quickly
I struggle to subtract correctly
Assessment
Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.9: We know this when the learner performs mental calculations.
1.25. To describe and illustrate different cultures' ways
of writing*
MATHEMATICS
Number Concept, Addition and Subtraction
Subtraction
EDUCATOR SECTION
Memorandum
Figure 1.45.

2.1 19 – 7 – 2 = 10
2.2 21 – 11 – 4 = 6
2.3 20 – 3 – 5 – 6 = 6
Leaner Section
Content
Activity: To describe and illustrate different cultures' ways of writing [LO 1.2]
Did you know?
The Mayas of Central America used numbers like these:
Figure 1.46.
1. We have already looked at how the Romans wrote. Now look closely at the writing of the Maya
Indians above and answer the following questions:
Table 1.32.
1.1 8: ............................................ 1.3 40: ...................................
1.2 14: .......................................... 1.4 43: ...................................
2. Calculate the following. Write your answers as we would write it.

Figure 1.47.
Assessment
Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.2: We know this when the learner describes and illustrates various ways of writing numbers in different cultures (including local) throughout history.
1.26. To use a series of techniques to be able to do
calculations*
MATHEMATICS
Number Concept, Addition and Subtraction
Subtraction
EDUCATOR SECTION
Memorandum
Leaner Section
Content

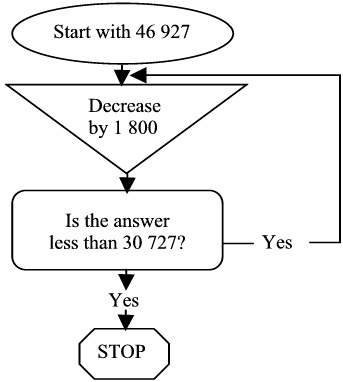
Activity: To use a series of techniques to be able to do calculations [LO 1.10]
1. A pocket calculator is very helpful in calculating answers, but it is useless if one does not understand what one reads. Work with a friend. Follow the steps of the flow diagrams and draw a circle around the first correct answer. First make sure that you know what to do!
Figure 1.48.
a)
b)
Figure 1.49.
Assessment
Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.10: We know this when the learner uses a range of techniques to perform written and mental calculations with whole numbers.
1.27. To examine and expand numeric patterns*
MATHEMATICS
Number Concept, Addition and Subtraction
Subtraction
EDUCATOR SECTION
Memorandum
1.1 6 550; 6 400; 6 250
1.2 14 345; 14 330; 14 285
1.3 122 500; 122 000; 120 500
Leaner Section
Content
Activity: To examine and expand numeric patterns [LO 2.1]
1. Do you still remember how to find "patterns" in number rows? (Learning Unit 1) Work on your own - without a calculator - and see whether you can complete the following number patterns
correctly:
1.1 6 850 ; 6 700 ; 6 550 ; .........................; .........................
1.2 14 360 ; ......................... ; ......................... ; 14 315 ; 14 300 ; ....................
1.3 122 500 ; ......................... ; 121 500 ; 121 000 ; ......................
Assessment
Learning Outcome 2: The learner will be able to recognise, describe and represent patterns and relationships, as well as to solve problems using algebraic language and skills.
Assessment Standard 2.1: We know this when the learner investigates and extends numeric and geometric patterns looking for a relationship or rules, including patterns:
2.1.1 represented in physical or diagrammatic vorm.
1.28. To determine the output values for given input
values*
MATHEMATICS
Number Concept, Addition and Subtraction
Subtraction
EDUCATOR SECTION
Memorandum
1.
a) 40
b) 420
c) 1 780
d) 24 270
3. less 40 because 19 + 1 = 20 and 21 – 1 = 20
PUZZLE
a) 41 and 42
b) 118 and 119
c) 88 and 89
d) 100 and 101
Leaner Section
Content
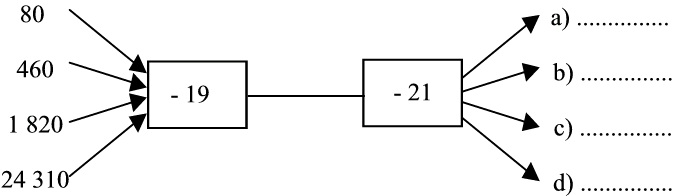
Activity: To determine the output values for given input values [LO 2.3]
1. Below is an example of a flow diagram. The numbers on the left are called input values, and the answers you have to provide are called output values. See whether you can complete the flow
diagram without the help of a calculator.
Figure 1.50.
2. Use a pocket calculator to check you answers.
3. How could you calculate the answers WITHOUT first subtracting 19 and then 21?
_____________________________________________________________________

_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
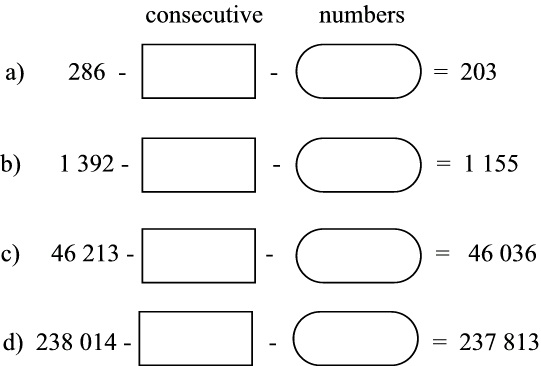
A PUZZLE
Consecutive numbers are numbers that follow directly after one another when you count, e.g. 22
and 23. Show whether you are able to figure out what the missing consecutive numbers are that
will make the following number sentences true:
Figure 1.51.
TIME TO DO SELF-ASSESSMENT
Colour in the picture that is true for you:
Figure 1.52.
Assessment
Learning Outcome 2: The learner will be able to recognise, describe and represent patterns and relationships, as well as to solve problems using algebraic language and skills.
Assessment Standard 2.3: We know this when the learner determines output values for given input values, using:
2.3.1 verbal descriptions;
2.3.2 flow diagrams.
1.29. To calculate by using selected computations*
MATHEMATICS
Number Concept, Addition and Subtraction
Subtraction
EDUCATOR SECTION
Memorandum
1.1 (a) 510 (b) 810 (c) 860 (d) 1 400 (e) 1 860
1.2 (a) 800 (b) 300 (c) 2 500 (d) 1 700
2.2
a) 16 00 - 10 000 = 6 000
b) 98 000 - 46 000 = 52 000
c) 642 000 - 23 6000 = 406 000
d) 926 000 - 759 000 = 167 000
e) 2468000 - 1129000 = 1339000
Leaner Section
Content
Activity: To calculate by using selected computations [LO 1.8]
1. As with addition we can subtract more easily by rounding off numbers. In this way we estimate what the answer should be approximately! Work with a friend. Take turns to say the answers out
loud to each other. Check the answers with a calculator. Feel free to ask your educator's help
where needed.
1.1 Subtract by rounding off both numbers to the nearest 10:
a) 567 – 63
b) 901 – 87
c) 885 – 25
d) 1 454 – 49
e) 1 999 – 138
1.2 Round both numbers to the nearest 100 and subtract:
a) 973 – 214
b) 1 259 – 993
c) 6 048 – 3 512
d) 9 999 – 8 234
2. Let us look at different ways in which the difference between big numbers can be calculated!
2.1 Can you still remember?
Explain to friend how to round off to the nearest 1 000.
2.2 Complete the table by rounding off to the nearest 1 000:
Table 1.33.
NUMBER 1
NUMBER 2
DIFFERENCE
e.g. 4 386 – 1 274
4 000
1 000
3 000
a) 15 980 – 9 621
.......................... .......................... ..........................
b) 98 102 – 46 147
.......................... .......................... ..........................
c) 642 368 – 236 419
.......................... .......................... ..........................
d) 926 135 – 758 910
.......................... .......................... ..........................
e) 2 468 265 – 1 128 651 .......................... .......................... ..........................
Assessment
Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.8: We know this when the learner estimates and calculates by selecting and using operations appropriate to solving problems;
1.8.1 rounding off to the nearest 5, 10, 100 or 1 000;
1.8.2 addition and subtraction of whole numbers with at least five digits.
Solutions
Chapter 2. Term 2
2.1. Multiplication*
MATHEMATICS
Grade 5
MULTIPLICATION AND DIVISION
Module 32
MULTIPLICATION
Activity 1:
To recognise and represent the multiples of single-digit numbers [LO 1.3.6]
I think you already know how important it is to know your tables well. In this learning unit it will help you to multiply quickly and correctly. Let us see how well you know your tables.
1. Take the fruit-shaped sweets containing the correct answers out of the jar. Colour them in
neatly and then write down the letter of the alphabet written on it. Use these letters to complete the sentence:
_____________ is a shorter way of doing repeated addition.
1.1 5 × 4
1.2 2 × 3
1.3 7 × 7
1.4 7 × 4
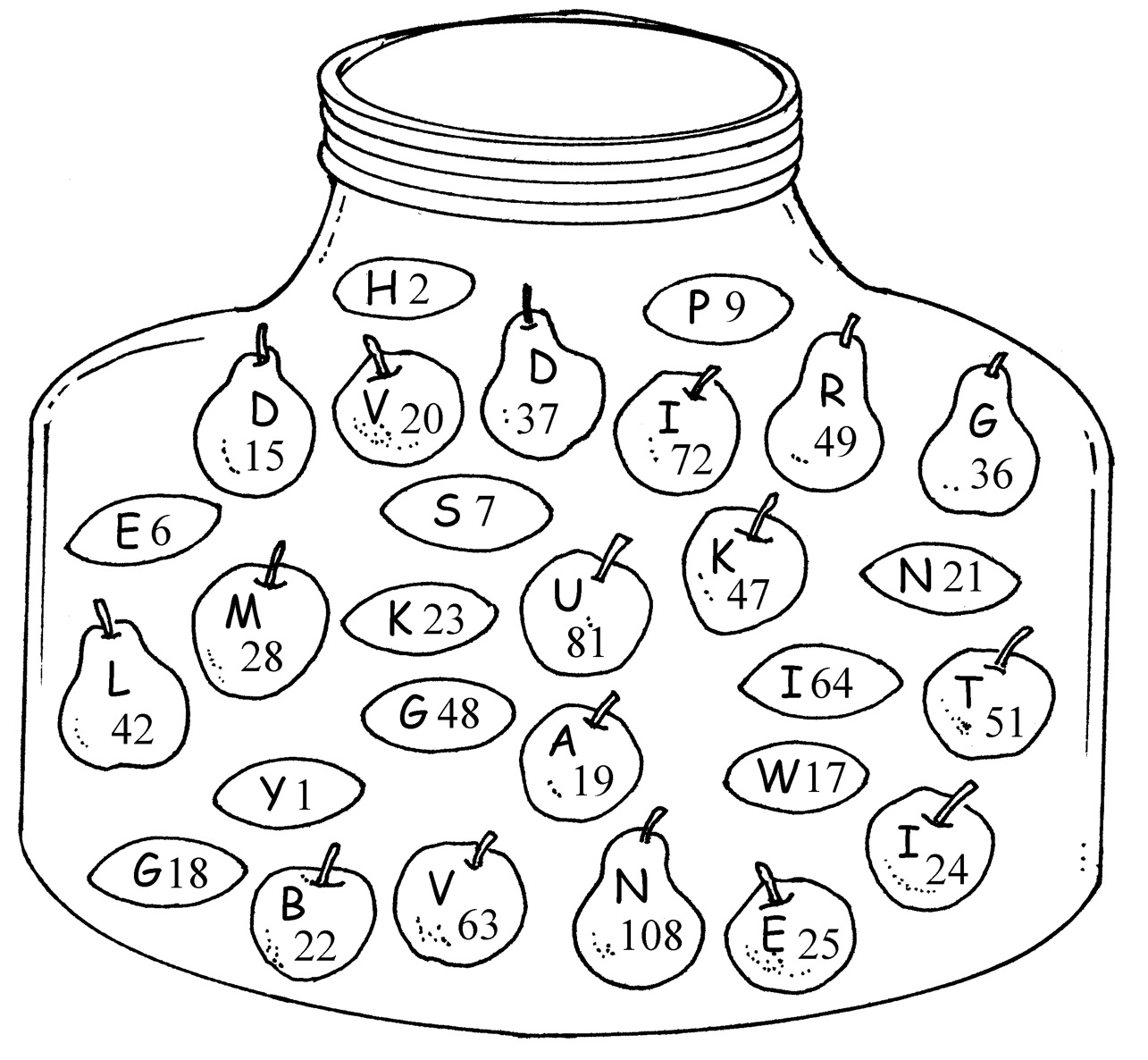
1.5 5 × 5
1.6 7 × 3
1.7 6 × 4
1.8 9 × 2
1.9 9 × 7
1.10 9 × 9
1.11 7 × 6
1.12 3 × 5
1.13 8 × 8
1.14 12 × 4
1.15 6 × 12
1.16 9 × 12
1.17 6 × 6
Figure 2.1.
Activity 2:
To recognise and represent the factors of at least any two-digit whole number
[LO 1.3.7]
1. Now that you know exactly what factors are, you are probably able to see their important function in multiplication. Factors also help us to test our answers when we multiply. Yes, you are right! We use them when we divide in order to test whether we have multiplied correctly. Now see how many pairs of factors you can write down for the following numbers.
Table 2.1.
a) 24 = ............ × ............ b) 36 = ............ × ............
= ............ × ............
= ............ × ............
= ............ × ............
= ............ × ............
= ............ × ............
= ............ × ............
= ............ × ............
2. Let us do some more exercises, using factors. Look at the products (numbers) and then write
down suitable factors for them. The first one has been done for you.
Table 2.2.
42
45
63
54
64
7 × 6
...................... ...................... ...................... ....................................
72
108
48
88
96
...................... ...................... ...................... ...................... ....................................
DO YOU STILL REMEMBER?
When you multiply any number by 0, the answer is always 0. (0 × 6 = 0)
Any number multiplied by 1, is that number.(9 × 1 = 9)
Activity 3:
To be able to do mental arithmetic [LO 1.9.2]
Now the factors are supplied to you. All you have to do in your first mental arithmetic test is to complete the multiplication block by writing down the missing answers only. Easy, isn’t it?
Table 2.3.
X 4
5
6
7
8
9
12
5 20
............ 30
............ 40
............ 60
6 ............ 30
36
42
............ 54
............
7 28
............ 42
............ 56
............ 84
8 ............ 40
............ 56
............ 72
............
9 ............ ............ 54
............ 72
............ 108
2 48
60
............ 84
............ 108
............
Activity 4:
To describe and illustrate different ways of writing in different cultures [LO 1.2]
By doubling numbers we can find the answer to a multiplication sum much more easily. Here we can learn from the Egyptians. Work with a friend and see whether you are able to find out how this calculation was done.
28 × 324
Table 2.4.
1 × 324:
324
(1 × 324)
Double 324:
648
(2 × 324)
Double l 648:
1 296 (4 × 324)
Double 1 296:
2 592 (8 × 324)
Double 2 592:
5 184 (16 × 324)
Thus: 28 × 324 = 9 072
BRAIN-TEASER!
Calculate the following in the same way as the Egyptians did thousands of years ago:
15 × 241
Is there an easier way of doing it? Discuss this with your friend. Check your answer with a
calculator.
DID YOU KNOW?
Thus we can also make use of DOUBLING when we want to multiply:
2 × 280 = (200 + 200) + (80 + 80)
= 400 + 160
= 560
Activity 5:
To use a series of techniques to do computations with whole numbers [LO 1.10.4]
1. If you looked carefully at the example above, you would have seen that this method of doubling differs from that of the Egyptians. Can you calculate the following by doubling it in exactly the same way?
1.1 2 × 1 430 =
1.2 2 × 2 315 =
2. We would very much like to use the shortest possible method in Mathematics, because it saves a lot of time, trouble and paper. Calculate the product again by doubling, but this time use a
shorter method if you can.
2.1 2 × 14 820 =
2.2 2 × 36 947 =
3. There is another technique that you can use to calculate the product. You can double and halve!
This makes it easier to multiply with the “big” numbers. Look carefully at the following:
126 × 5= 63 × 10 (halve 126 ; double 5)= 630
Can you find the following answers by doubling and halving?
Table 2.5.
3.1 50 × 24 3.2 5 × 346
BRAIN-TEASER!
Can you fill in the missing numbers/factors WITHOUT using your calculator?
Table 2.6.
48
× 12
= 576 64
× 10
= 640
........... × 24
= 576 32
× ........... = 640
12
× ........... = 576 ........... × 40
= 640
6
× ........... = 576 8
× ........... = 640
........... × ........... = 576 ........... × ........... = 640
Did you discover a pattern?
Activity 6:
To calculate by using selected computations [LO 1.9.2]
1. Now let us look at multiplication with multiples of 10 and 100. As we work through the examples, you will see that there are certain rules that you must follow in order to calculate the product. If you apply these rules, you will be able to calculate the answers without doing long computations on paper. Work with a friend and write down the product of the following:
1.1 10 × 6 = ......................... ; 10 × 60 = ......................... ;
10 × 600 = ......................... and 10 × 6 000 = .........................
1.2 10 × 9 = ......................... ; 10 × 90 = ......................... ;
10 × 900 = ......................... and 10 × 9 000 = .........................
1.3 10 × 15 = ......................... ; 10 × 150 = ......................... ;
10 × 1 500 = .........................
1.4 10 × 26 = ......................... ; 10 × 260 = ......................... ;
10 × 2 600 = .........................
Can you now write down a rule for multiplying any number by 10?
Does this “work” for 0,5 × 10?
2. Let us look at multiplication with multiples of 100. Work with the same friend and write down the product of:
2.1 100 × 8 = ......................... ; 100 × 80 = ......................... ;
100 × 800 = .........................
2.2 100 × 13 = ......................... ; 100 × 130 = ......................... ;
100 × 1 300 = .........................
2.3 100 × 27 = ......................... ; 100 × 270 = ......................... ;
100 × 2 700 = .........................
Write a rule for multiplying any number by 100:
Does your rule “work” for 0,2 × 100?
Activity 7:
To recognise and use the characteristics of multiplication with whole numbers
[LO 1.12.3]
1. In our previous module we looked at the associative and commutative characteristics of
addition – do you remember this? There are similar characteristics of multiplication. Do you want to know how it works? Fill in the missing factors to balance the equasions:
8 x 6 = 6 x ____
23 x ____ = 13 x 23
124 x 85 = ____ x 124
2. Is the following true or false?
2.1 6 × 3 × 4 = 3 × 4 × 6 = 4 × 6 × 3 ..................................................
2.2 (2 × 4) × 5 = (5 × 4) × 2 = 4 × (2 × 5) ..................................................
3. What do you realise from the above examples?
Activity 8:
To estimate and calculate by means of rounding off [LO 1.8.1]
1. To be able to estimate answers is an important skill. If you are good at estimating, it will be easier for you to realise that you may have made a mistake in your calculations. Round off the following numbers first and in this way you will be able to estimate what the product of each of the following will be:
Table 2.7.
SUM
ESTIMATE
CALCULATOR DIFFERENCE
E.g. 19 × 21 400
399
1
a) 38 × 27
......................... ......................... .........................
b) 99 × 146 ......................... ......................... .........................
c) 45 × 69
......................... ......................... .........................
d) 998 × 78 ......................... ......................... .........................
e) 409 × 18 ......................... ......................... .........................
BRAIN-TEASERS!
a)Which two numbers, smaller than 10, have 3 factors each?
......................... and .........................
b) Colour in the correct block:
Table 2.8.
Table 2.8.
The product of 2 uneven numbers is always an EVEN UNEVEN number.
c) Which two numbers have a product of 48 and a sum of 16?
......................... and .........................
Activity 9 :
To be able to solve problems in context [LO 1.6.1]
To be able to use a series of techniques to do calculations [LO 1.10]
Let’s do some brainstorming now. Your teacher will give you the necessary paper.
1. Split up into groups of three and, as quickly as possible, make a list of all the means of
transportation that exist in our country.
2. Which of the above-mentioned would you choose if you had to travel? Why?
3. Where is your favourite seat in:
1. a car
2. a school bus
3. a boat
4. an aeroplane
4. Now see whether you are able to solve the following problems:
Messrs Slobo, Mugathle and Sisula have each bought a brand new taxi with which to transport
passengers. For their first trip their plans are the following:
Table 2.9.
Owner
Amount per person Number of passengers km travelled
Slobo
R15,80
13
76
Mugathle R14,60
14
84
Sisula
R16,25
12
59
Who made the most money with the first trip?
If the petrol cost R1,05 for every kilometre that was travelled, how much did Mr Mugathle’s












