6.
______
How do the answers of 3 and 4 differ from the rest?
Why is this?
Did you know?
Normally we don’t write the noughts at the end of decimal fractions, but in the following cases we do:
a) When we work with money: R8,60 (shows how many cents there are).
b) When we time an athlete with a stop-watch: 7,30 seconds. This is how we give results to the hundredth of a second.
1. When Mom buys material: 1,70 m (so that the saleslady knows exactly how many cm to cut).
Activity 2:
To recognise and represent numbers [LO 1.3.3]
1. It is sometimes difficult to determine exactly where a decimal number fits into the greater
whole. A number line is a handy way of helping you to determine this, because it helps you to
“see” the sequence of the numbers. Draw arrows and label with the letters given to indicate more or less where the following numbers will be on the number line:
Figure 3.26.
A : 5,82



B : 5,99
C : 6,09
D : 6,24
Activity 3:
To use a series of techniques to do mental arithmetic [LO 1.10.2]
1. Let us play a game!
Work with a friend. Take turns. Close your eyes and press on any number in the diagram on the
next page with the back of your pencil. Open your eyes and tell your friend what the number
consists of:
e.g. 14,38 = 14 + +
Colour in every number you get right green. Your friend colours all his / her correct numbers blue.
The one who has something wrong misses a turn. The one who has coloured in the most blocks,
wins.
Figure 3.27.
Activity 4:
To recognise and classify numbers in order to compare them [LO 1.3.3]
1. By now you know how to write tenths and hundredths as decimal fractions. Look very carefully at the following numbers. Replace the * with < , > or =.





Hint: You should break the numbers up as in the game above if you have any doubts about the
correct answer.
1.1 1,7 * 1,07 _____
1.2 0,6 * 0,06 _____
1.3 0,58 * 0,9 _____
1.4 0,34 * 0,4 _____
1.5 2,05 * 2,5 _____
1.6 1,8 * 1,80 _____
Brain-teaser!
What does one quarter ( ) look like as a decimal fraction?
Can you write the following as decimal fractions?
a) : _____
b) : _____
c) : _____
d) : _____
Activity 5:
To use tables and checks in order to arrange and record data [LO 5.3]
1. Challenge!
Take a measuring tape and measure the height of five of your class mates (to 2 digits after the decimal comma). List your results in a table and number your friends from the shortest to the
tallest.
Table 3.21.
Name Height Numbered:short to tall



1.1
1.2
1.3
1.4
1.5
THOUSANDTHS
Did you know?
When I write one thousandth
as a decimal fraction, it will be 0,001.
The noughts are place holders for the units, tenths and hundredths and may not be left out.
Figure 3.28.
Activity 6:
To recognise, classify and represent numbers in order to describe and compare
them [LO 1.3.3]
1. Look carefully at the representations below. Which decimal numbers are represented in each
one?
E.g.
Table 3.22.
U t
h th
X
X
X
X
X X
X X X X
1.1
Table 3.23.
U t h th
X
X
X
X
X
X
X
X X X
X X X
1.2
Table 3.24.
U t h th
x
x
x
x x
x x x
x x x
1.3
Table 3.25.
U t h th
x
x
x x
x x
x x x
x x x
x x x
1. Can you write the above as mixed numbers / common fractions?
Activity 7:
To recognise, classify and represent numbers in order to describe and compare
them [LO 1.3.3]
1. Colour in only the bags that are heavier than 1,5 kg:
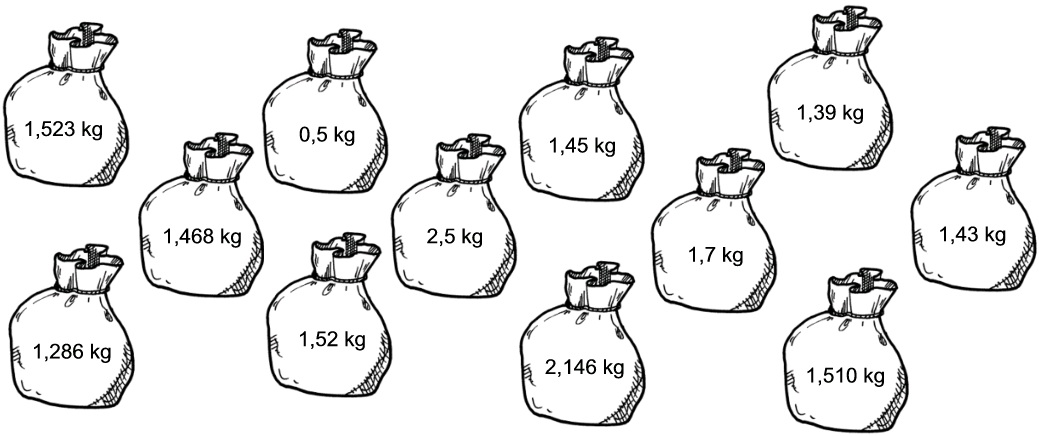


Figure 3.29.
2. In Module 1 we spoke a lot about the value and place value of numbers. (Do you remember?)
Look carefully at the following numbers and then write down the value of each number that has
been underlined:
E.g. 3,768 :
2.1 4,231 : _____
2.2 8,923 : _____
2.3 289,7 : _____
2.4 21,38 : _____
2.5 57,236 : _____
2.6 9,897 : _____
3. Compare the following numbers. Draw a circle around the smallest one.
Hint: You may change them to ordinary fractions / mixed numbers if you like – this may help you to get the answer more easily!
3.1 0,6 ; 0.06 ; 0,006
3.2 3,2 ; 0,32 ; 0,032
3.3 1,101 ; 1,111 ; 1,110
Brain-teaser!
What does one eighth ( ) look like as a decimal fraction?





And ?_____ And ? _____ And ?._____
Can your write
as a decimal fraction? .
What does
look like as a decimal fraction?
Explain how you got these answers WITHOUT using the calculator!
Assessment
Table 3.26.
Learning outcomes(LOs)
LO 1
Numbers, Operations and RelationshipsThe learner is able to recognise, describe and represent
numbers and their relationships, and to count, estimate, calculate and check with competence
and confidence in solving problems.
Assessment standards(ASs)
We know this when the learner:
1.3 recognises and represents the following numbers in order to describe and compare them:
1.3.3 decimal fractions of the form 0,5; 1,5; 2,5, and so on, in the context of measurement;
1.5 recognises and uses equivalent forms of the numbers listed above, including:
1.5.2 decimal fractions of the form 0,5, 1,5 and 2,5, and so on, in the context of measurement; 1.6 solves problems in context including contexts that may be used to build awareness of other
Learning Areas, as well as human rights, social, economic and environmental issues such as:
measurements in Natural Sciences and Technology contexts;
1.8 estimates and calculates by selecting and using operations appropriate to solving problems
that involve:

(additional) addition of positive decimals with 2 decimal places;
1.9 performs mental calculations involving:1.9.1 addition and subtraction;1.9.2 multiplication of whole numbers to at least 10 x 10;
1.10 uses a range of techniques to perform written and mental calculations with whole numbers
including:
building up and breaking down numbers;
using a calculator;
1.11 uses a range of strategies to check solutions and judge the reasonableness of solutions;
LO 2
Patterns, functions and algebraThe learner will be able to recognise, describe and represent
patterns and relationships, as well as to solve problems using algebraic language and skills.
We know this when the learner:
2.6 determines, through discussion and comparison, the equivalence of different descriptions of the same relationship of rule presented
2.6.3 by number sentences.
We know this when the learner:
2.6 determines, through discussion and comparison, the equivalence of different descriptions of the same relationship of rule presented
2.6.3 by number sentences.
We know this when the learner:
5.3 organises and records data using tallies and tables;
Memorandum
ACTIVITY 1
1. 1.1
= 0,36





1.2
= 1,07
1.3
= 3,6 / 3,60
1.4
= 42,85
1.5
= 47,03
BRAIN-TEASER!
1. 0,03
2. 0,09
3. 0,4
4. 0,8
5. 0,37
6. 0,59
Only one digit after the comma.
Pocket calculator does not show the last nought.
ACTIVITY 2
1.
A B C D
Figure 3.30.
ACTIVITY 4
1. 1.1 >
1.2 >
1.3 <
1.4 <








1.5 <
1.6 =
BRAIN-TEASER!
a) 0,75
1. 0,04
2. 0,15
3. 0,34
ACTIVITY 6
1. 1.1: 5,026
:2,603
:0,359
2. 2.1: 5
2.2: 2
2.3:
ACTIVITY 7
1. 1,523; 1,52; 2,5; 2,146; 1,7; 1,510; 3,5
2. 2.1
2.2
2.3
2.4 20
2.5
2.6
3. 3.1 0,006
3.2 0,032
3.3 1,101
BRAIN-TEASER!
0,125; 0,375; 0,625; 0,875
0,448
0,7
Change denominator to 1 000 (equivalent fractions)
3.6. Solve problems in context*
MATHEMATICS
Grade 5
ORDINARY FRACTIONS AND DECIMAL FRACTIONS
Module 50
SOLVE PROBLEMS IN CONTEXT
ACTIVITY 1:
To solve problems in context [LO 1.6.2]
1. Split up into groups of three. Find the solutions to these problems without using your pocket calculator.
A farmer wants to build a chicken coop with perches and needs the following timber for the
job:




















one plank of 4,3 m
one plank of 2,58 m
one plank of 3,26 m
What is the total length of all the planks that he needs?
1.2 In a certain residential area trees have to be cut down because they are touching the telephone wires. If they cut 0,259 m from the one tree, 1,5 m from the next and 2,93 m from the third tree, how many metres have been removed from the trees altogether?
1.3 Three buildings have to be painted. If one of the buildings is 16,8 m tall, the second one is 23,495 m tall and the third one is 46,77 m tall, how many metres have to be painted in all?
Activity 2:
To determine the equivalence and validity of different representations of the
same problem through comparison and discussion [LO 2.6.3]
ADDITION OF DECIMAL FRACTIONS
1. In Activity 2.15 you had the opportunity of solving problems by using your own methods and
techniques. Now you must work with a friend. Read the problem and then work through the
different solutions of the various learners.
Three buildings are 58,2 m; 63,54 and 39,249 m high respectively. How high are they altogether?
1.1 I must calculate 58,2 + 63,54 + 39,249:
It is precisely the same as 58 + + 63 + +
+ 39 + +
+
I add the whole numbers first: 58 + 63 + 39 = 160
Then I add all the tenths: + + =
Then I add the hundredths:
+
=
Lastly, I add everything together: 160 + +
+
= 160 +
+
+
= 160
= 160,989
1.2 I use notation columns to calculate the sum of 58,2; 63,54 and 39,249:
Table 3.27.
T
U t h th
5
8 2
6
3 5 4
3
9 2 5 5
16 0 9 8 9
The three buildings are 160,989 m high altogether.
1.3 I must calculate 58,2 + 63,54 + 39,249.
I do it exactly like a normal addition sum but I remember to keep the commas precisely
underneath each other!
58,200
63,540
+ 39,249
160,989
2. Which method do you choose?
Why?
3. How do the first two methods compare with each other?
Activity 3:
To calculate by means of selection and through the use of suitable computations
(additional) [LO 1.8]
1. Let us see how well you do on your own. Calculate the following without using a pocket
calculator:
1.1: 3,247 + 117,9 + 36,58
1.2: 2,36 + 18,459 + 23,7
1.3: 5,742 + 87,62 + 49,136
1.4: 48,5 + 231,8 + 9,826
2. Try to do the following without any calculations: A farmer wants to fence his camp with wire but he only has loose pieces of wire. He has a piece of 2,5 m, another piece of 0,5 m and a third piece of 1,5m. How much wire does the farmer have altogether?
3. Explain to a friend how you calculated your answer!
4. Check all your answers of 1 and 2 with a calculator.
Brain-teaser!
Can you solve the following magic squares? You may use your calculator!
Table 3.28.
0,6 0,1
0,5
0,4
Table 3.29.
2,6
2,3
2
2,2
Activity 4:
To solve problems in context [LO 1.6.2]
1. Split up into groups of three. Your teacher will tell you which one of the problems below must be solved by your group. You will also be given the necessary paper to work on. Remember: no
pocket calculators!









Taxi A needs 36,78 litres of petrol to fill its tank. Taxi B needs 29,9 litres. How many more
litres of petrol does taxi A need?
Mrs Mmbolo is making curtains for her school’s new classrooms. If she needs 172,5 m of
material for the ground floor and 98,75 m for the top storey, what is the difference in metres
between the material needed for the two floors?
After the rainy season two dams on a farm held 459,23 kℓ and 263,587 kℓ of water respectively.
What is the difference between the amount of water in the two dams? Give your answer in kℓ.
The difference in mass between two animals in the Kruger National Park is 4,963 kg. If the
heavier animal has a mass of 75,23 kg, what is the mass of the other one?
2. Now compare your answer with that of a group that had to solve the same problem.
3. Explain your solution to the rest of the class.
4. Have a class discussion on the differences / similarities in your methods.
Activity 5:
To use a series of strategies to check solutions and to assess the reasonableness of
the solutions [LO 1.11]
1. We have just solved a few problems and discussed the different ways to determine the answers.
Work with a friend, read the following problem and take a good look at the given solutions. Make sure that you understand how the answer has been calculated.
ADDITION
A restaurant uses 9,786 ℓ milk during breakfast and 5,463 ℓ for supper. How much less milk is used for supper?
1.1 I must calculate 9,786 – 5,463
I first subtract the whole numbers: 9 – 5 = 4
Then I subtract the thousandths:
−
=
Now I subtract the hundredths:
−
=
Lastly I subtract the tenths: − =



Now I add the answers: 4 + +
+
= 4.323
The difference is thus 4,323 ℓ.
1.2 I do it in precisely the same way as normal subtraction but I write the commas precisely underneath each other:
9,786
− 5,463
4,323
The restaurant uses 4,323 ℓ less milk at supper time.
2. Whose method do you choose?
Why?
Activity 6:
To calculate through selection and the use of suitable computations (additional)
[LO 1.8.8]
1. Now use any method and calculate the following without a calculator:
1.1: 6,42 - 2 98
1.2: 7,23 - 4,57
1.3: 8,123 - 3,545
1.4: 9,236 - 3,457
2. Check your answers with a calculator.
Brain-teaser!
Calculate 5 – 1,426
Activity 7:
To solve problems in context [LO 1.6.2]
Here is a challenge!
This assignment can be placed in your portfolio. Make sure that you read the criteria for
assessment very carefully before you start. Ask your teacher for the necessary paper.
1. Look for examples of decimal fractions in your local newspaper or your favourite magazine.
Cut them out neatly and paste them in below.





































































