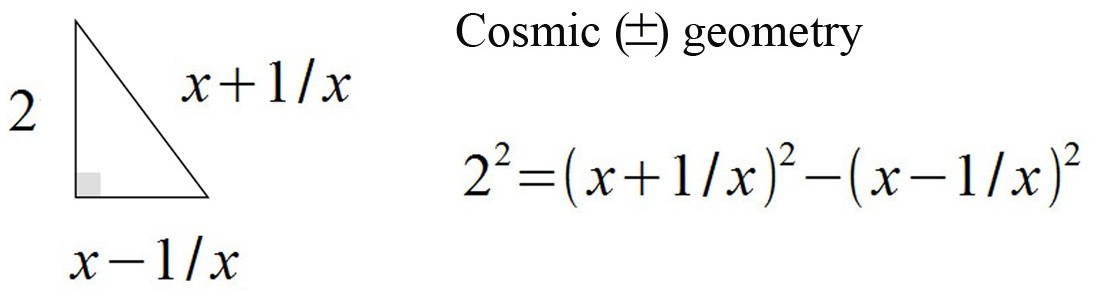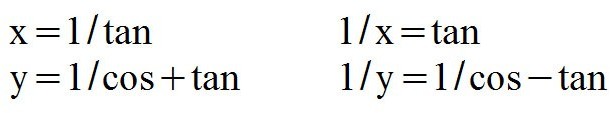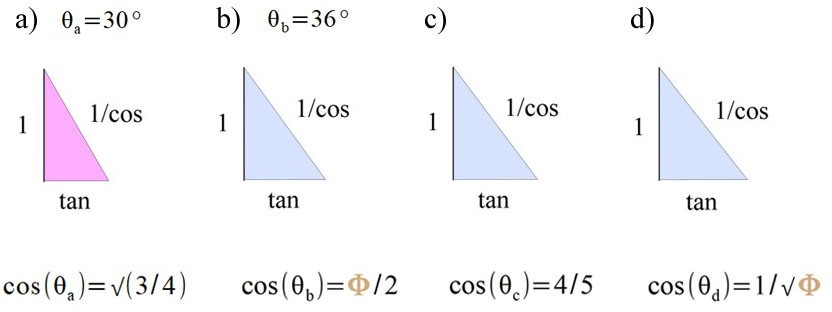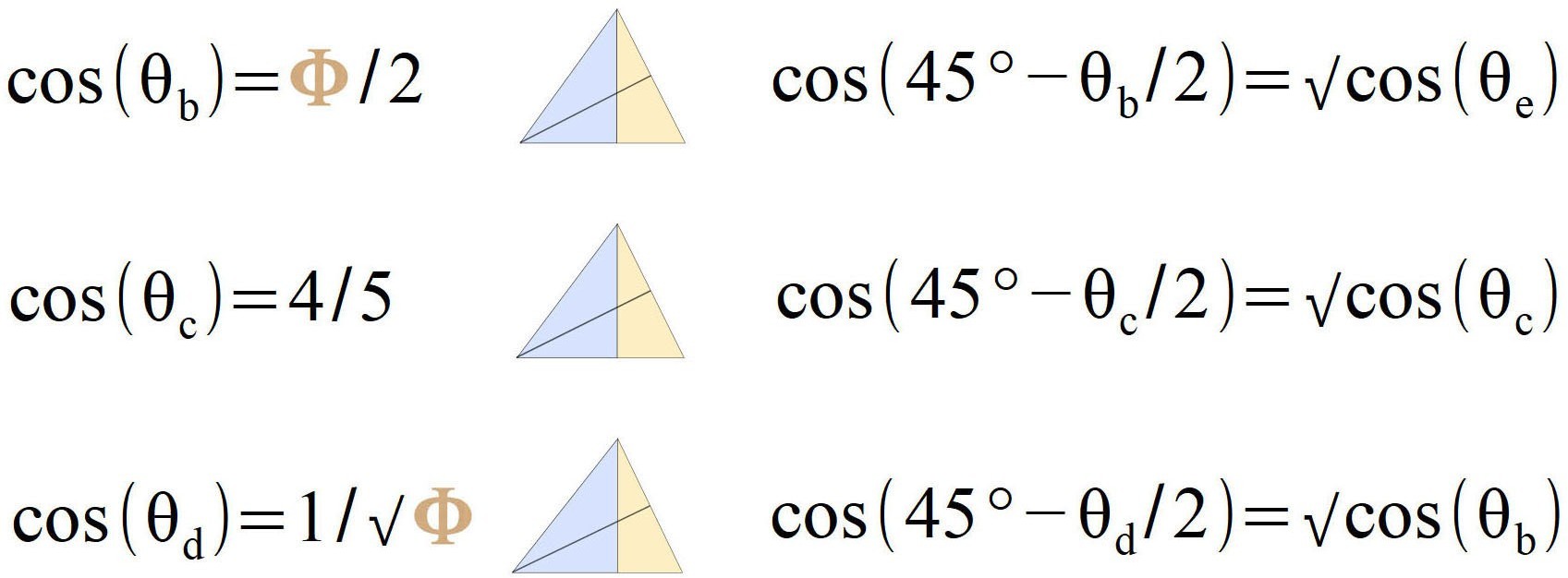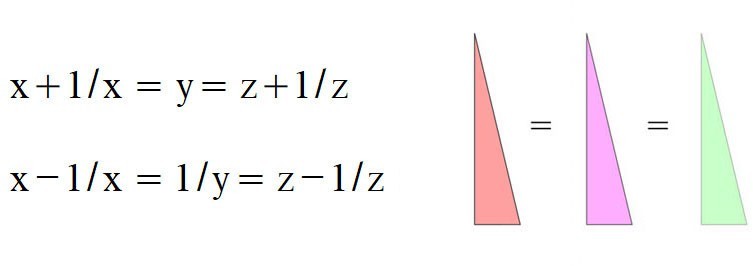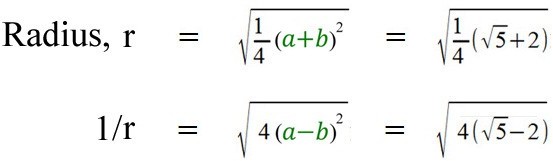The amazing world of the golden ratio (phi) - part 2 by Folding Circles - HTML preview

Cosmic Geometry (±)

A method based on a simple equation that gives valuable insight into the nature of geometry and its hidden beauty.

Using this method, we can detail the geometry of a triangle without using trigonometry or Pythagoras's theorem.

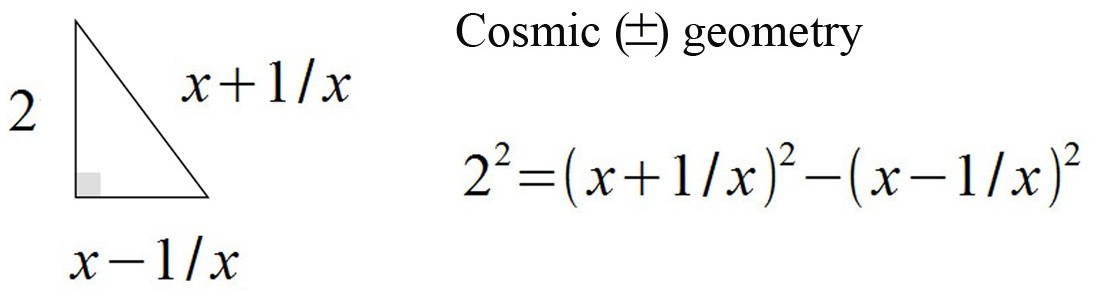
It adds a level of sophistication to the normal method.

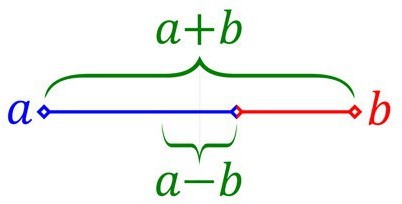
Taking into account the negative principle is a bit of a mind- bender, so, patience is a virtue.

The most interesting cosmic number is (phi) golden ratio.

The basic geometry of a circle, showing roots and reciprocals.

Some basic examples using cosmic mathematics, shown below.

This yellow triangle is a special golden ratio triangle.

This method uses both the left and right sides of your brain, so expect to struggle and take your time with these examples.

Do more examples in your own time, there is no rush. method may be simple but it is also extremely sophisticated. Some basic examples of scaling with the 345 triangle.

You are going to need a basic knowledge of geometry, a sharp pencil, lots of paper and pocketfuls of patience.

The following method works for all right angled triangles.

For brevity the following substitutions will be used, sometimes.

found in the blue triangle as shown below.

The value of the reciprocals x and y for all angles.

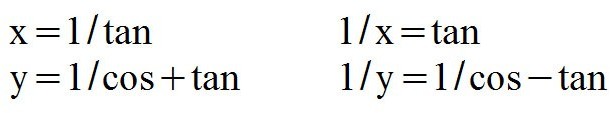
The relationship between the angles is shown below.

geometry called the power of a point, as shown below.

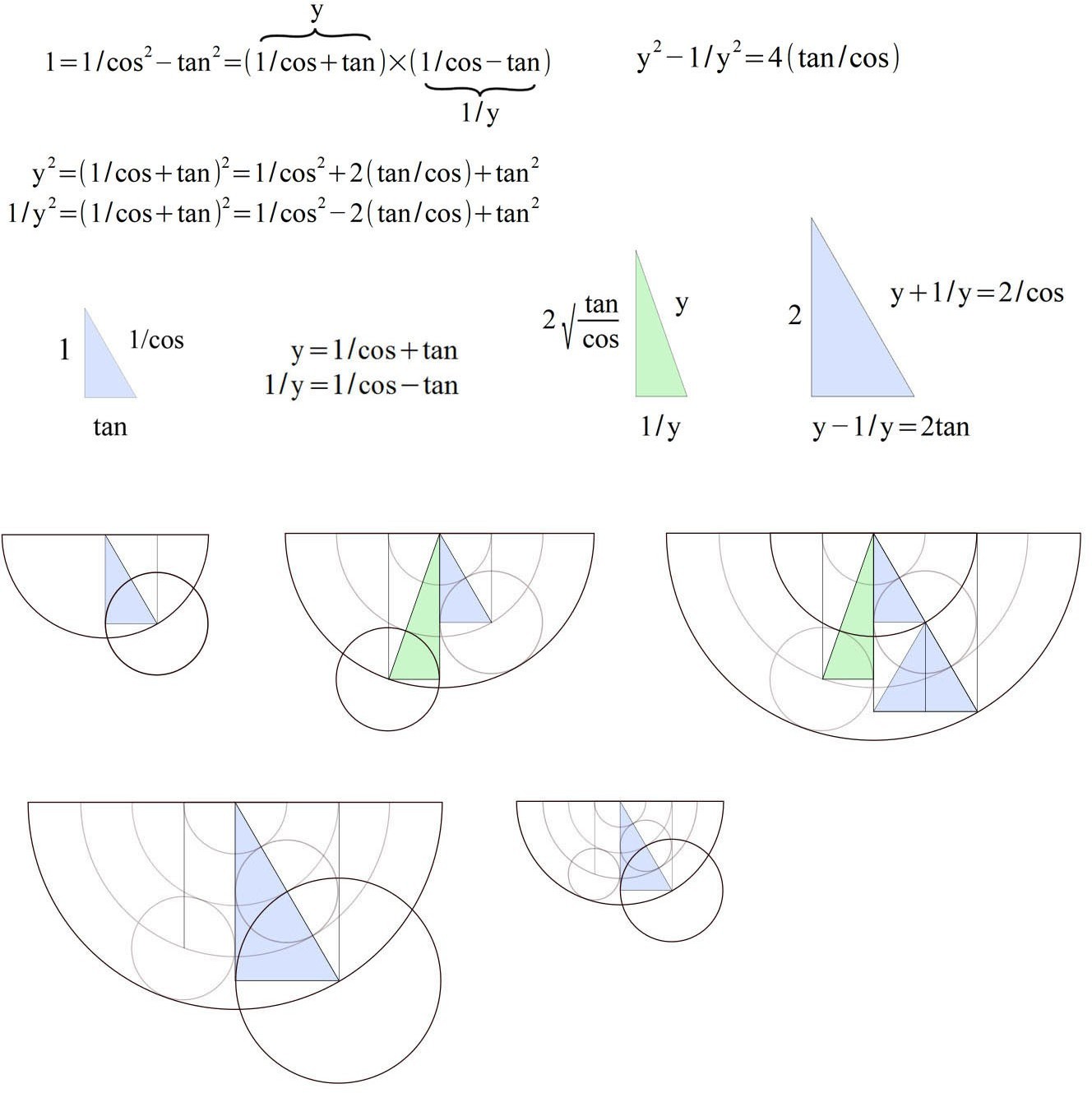
This gives us the following set of four coloured triangles.

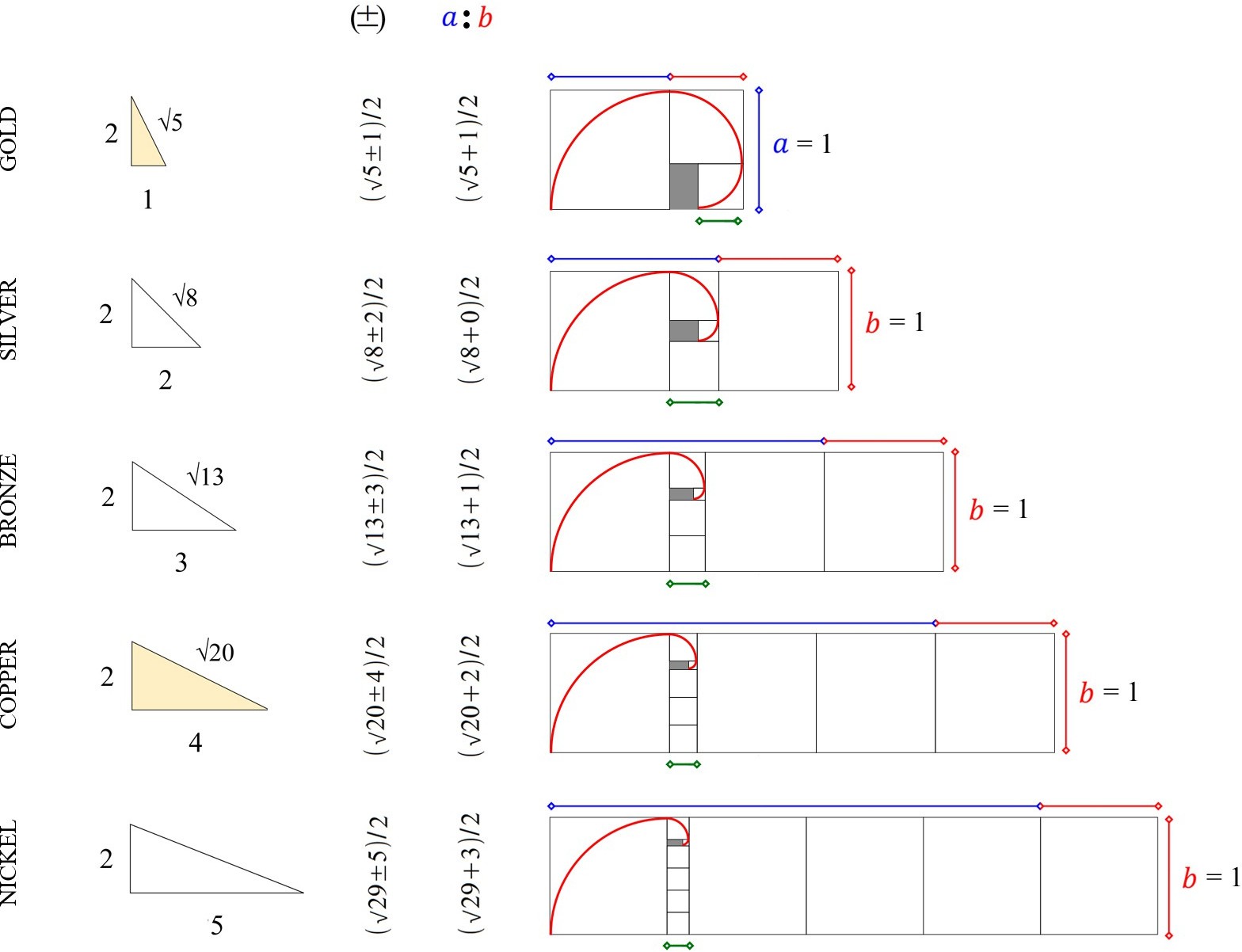
The base of green and yellow triangles always has a (2:1) ratio.

Angle (a) is special because the blue, red and yellow triangles are all equal, hence the different colour, as shown below.

The final triangle is this scaled version of the green triangle.

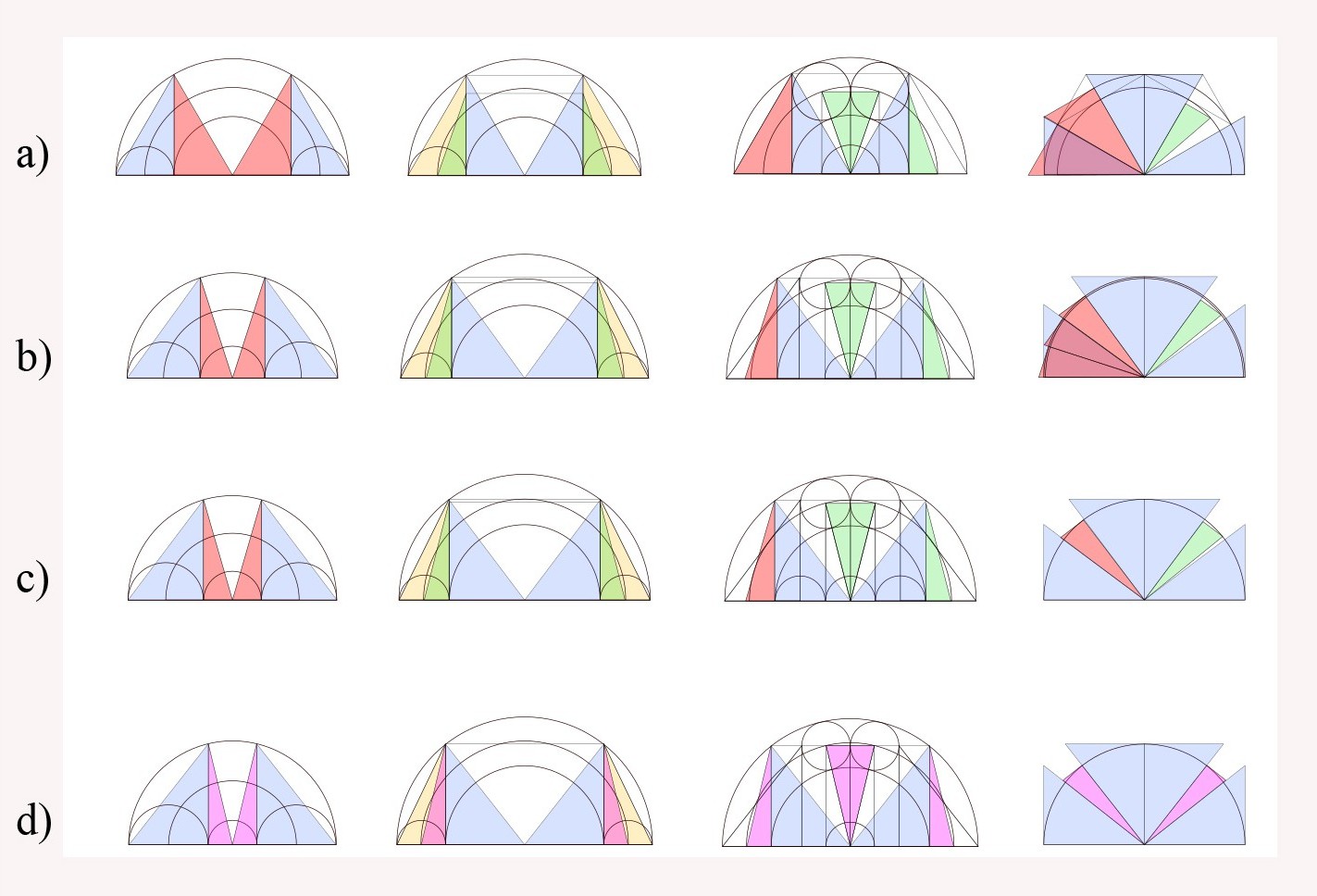
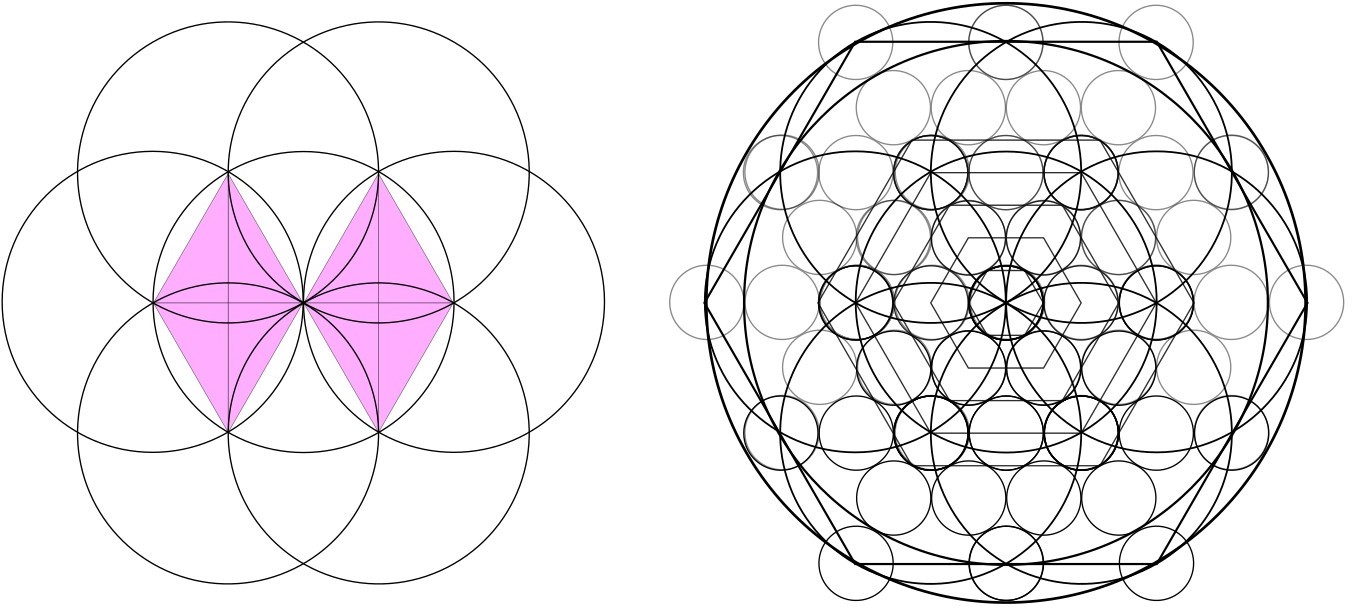
Angle (a) gives us the geometry of the vesica piscis, and six circles around a hexagon with perimeter=6, as shown below.

This following beautiful geometry is known as the flower of life.

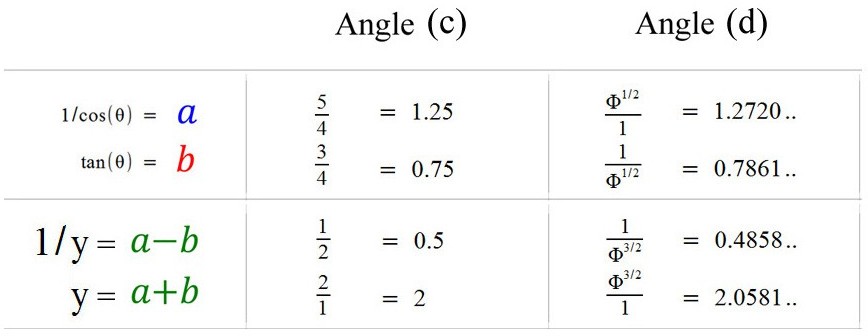
The next three angles have an interesting phi relationship.

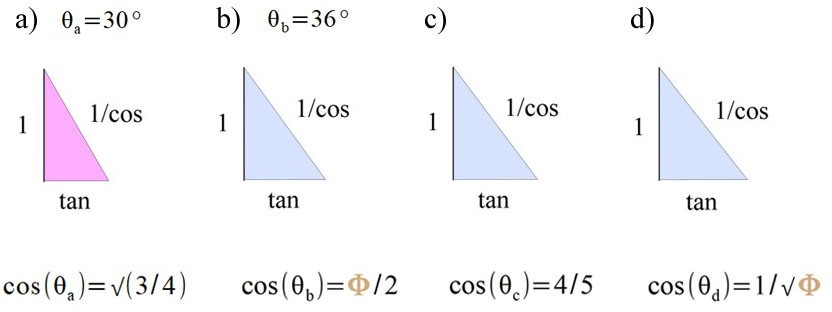
Angle (b) gives us the geometry of the pentagon, which we can construct using the red and blue triangles, as shown below.

The golden ratio is unique because of the following.

Below we can see both sets giving us five golden ratio rings.

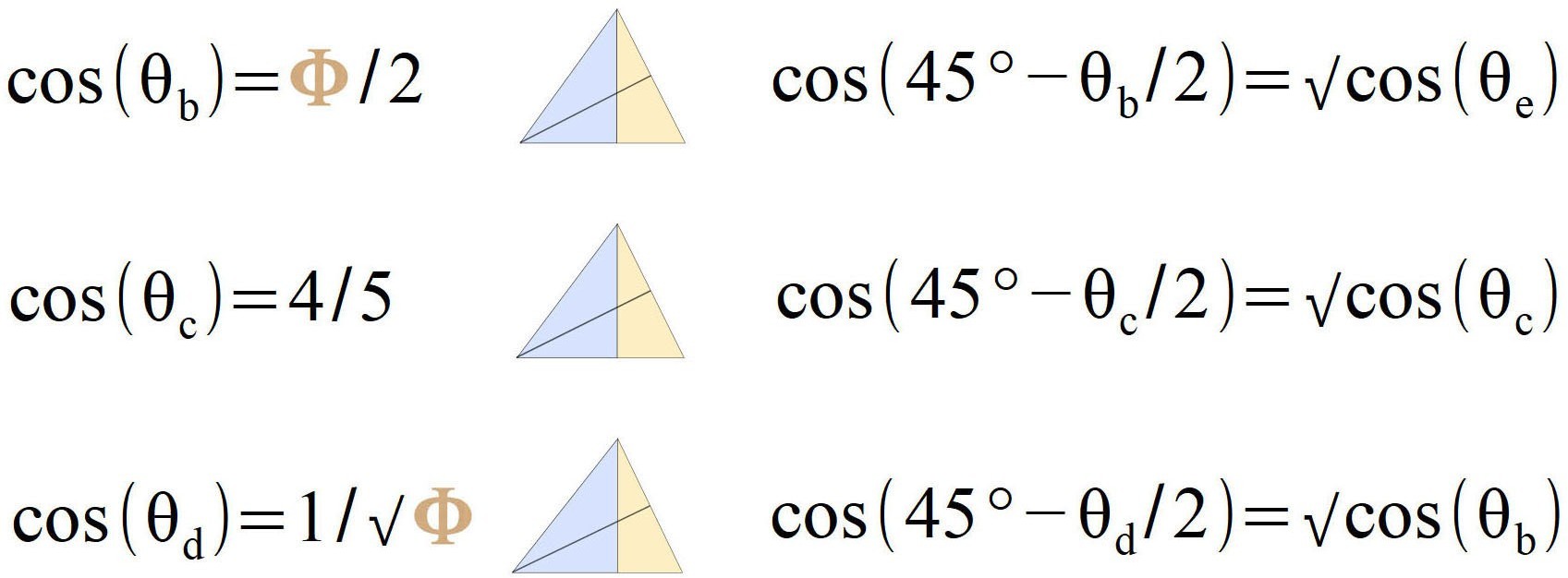
Next we detail the same angles as rectangles with (y:1) ratios.

Angle (c) gives a perfect half-square or rectangle with (2:1) ratio.

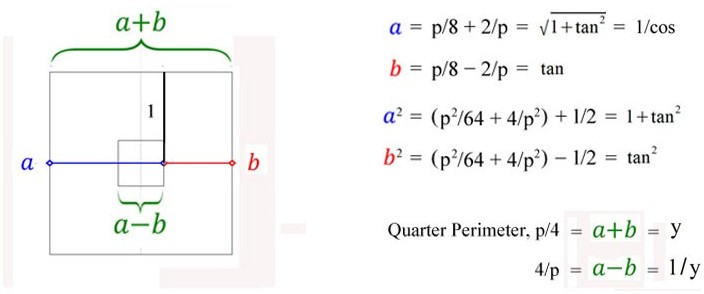
And the square numbers, or geometric progression (1,2,4,8,16,..) and reciprocals with ratio (2:1) where y=2 and perimeter=8.

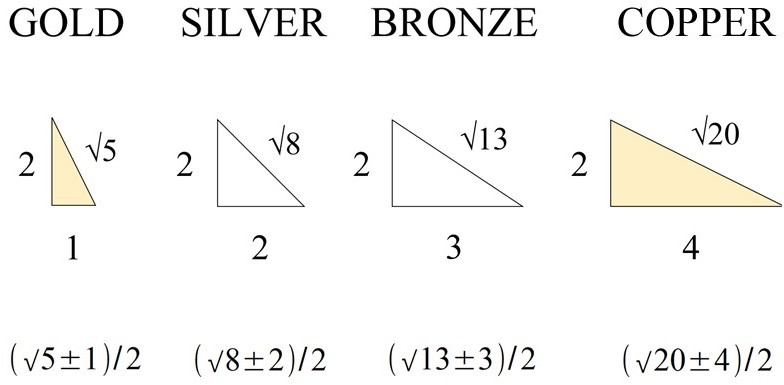
From it we get the 345 and golden (phi) triangles, shown below.

The 345 triangle is very special indeed, as shown below.

The green and pink triangles have a phi relationship, the pink and yellow triangles have a square-root relationship with the blue.

A picture speaks a thousand words. Silence, an infinity.

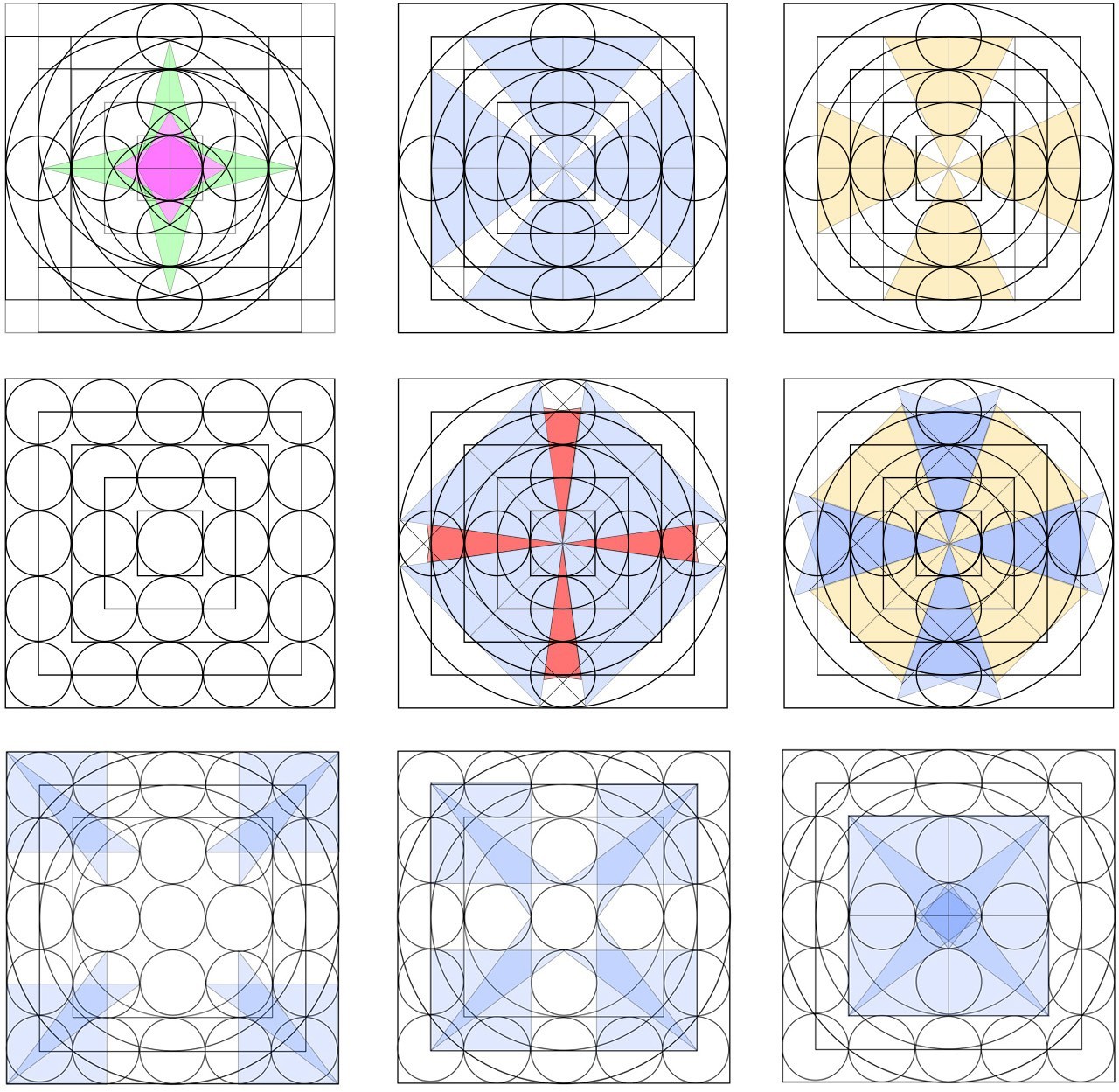
The geometric link between the fruit of life and the square.

triangles are equal, hence the different colour.

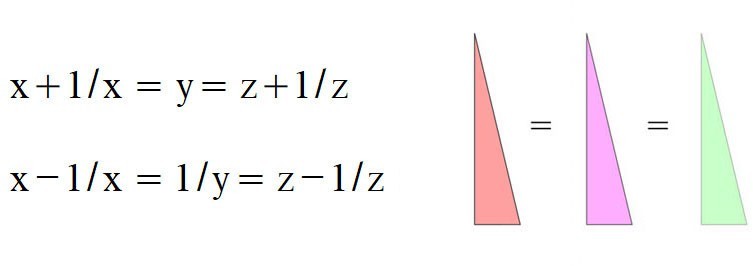
This is because cos and tan are equal, as shown below.

And so uniquely a and b are reciprocals, therefore.

This is very special indeed and means that using this method, only this angle gives us the geometry of a circle, as shown below.

All decimals used in this book can be written as fractions.

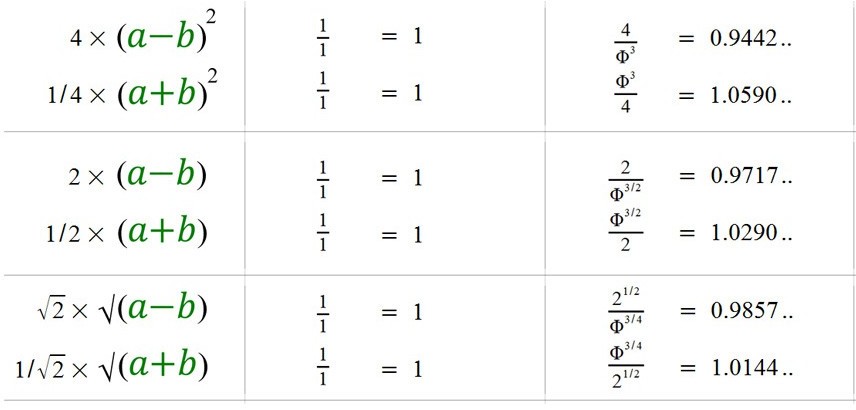
It gives us this very special sequence of numbers based on root 5.

Where the multiplication factor is equal to the radius, as shown.

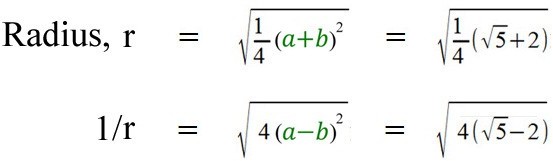
Metallic mean 1 and 4 are both based on the magical root 5.

This relationship to the square numbers (sn) is shown below.

We can scale the triangle in the following roundabout way.

Which brings us to the next level of cosmic mathematics.

The 345 triangle is very special case of Pythagorean triple.

Pythagorean triples using cosmic geometry, as shown below.

Cosmic geometry can be found all over the place.

And the relationship between them, known as Binet's formulas.

Notice how the two number sequences cross over at some point

As you can see, this number is magical to the extreme.

Metallic means 1-5 using cosmic geometry, as shown below.

Spirals made from quarter circles, rectangles made from squares.

The amazing world of (phi) the golden ratio or the golden thread.

you have learnt with the following two interesting angles.

Using the method in this book means that every number, apart from the magical number discussed, has two angles.

And each angle has related blue and green triangles.

Good luck on your journey, always keep your compass at hand in case of storms and make sure to choose a good path.

Does the path have a heart? If it does, the path is good. does is done using circles (cycles and spirals).

The geometry that includes the vesica piscis and the flower of life has always been known as sacred geometry (cosmic geometry).

Share this knowledge with your tribe and together we will restore faith and wonder back to the lost children of this precious earth. Be a world child and form a circle before we all go under.