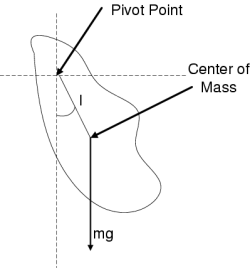
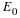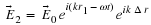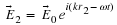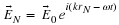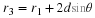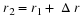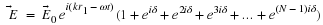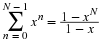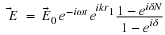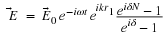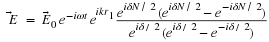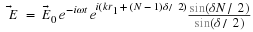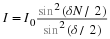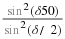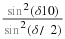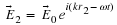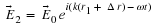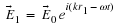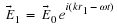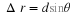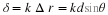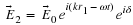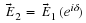The Simple Harmonic Oscillator
For SHM to occur we require stable equilibrium, about a point. For example, at
the origin we could have:
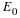 which
would describe a system in equilibrium. This however is not necessarily stable
equilibrium.
which
would describe a system in equilibrium. This however is not necessarily stable
equilibrium.
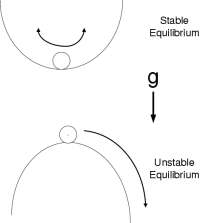
The lower part of the figure shows the case of unstable equilibrium. The upper
part shows the case of stable equilibrium. These situations often occur in
mechanical systems.
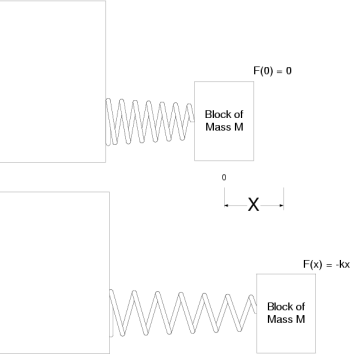
For example, consider a mass attached to a spring:
In general, in a case of stable equilibrium we can write the force as a
polynomial expansion:
F
(
x
)
=
−
(
k1x
+
k2x2
+
k3x3
+
…
)
where
the
ki
are positive constants. There is always a region of
x
small enough that we can write:
F
=
−
k
x
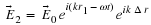 This is satisfied by an equation of the form
x
=
A
sin
(
ωt
+
φ0
)
where
A
and
φ0
are constants that are determined by the initial conditions.
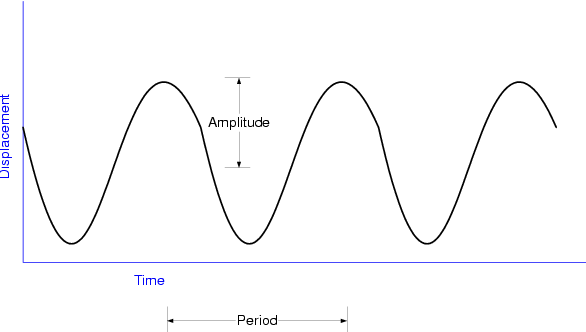
Draw a diagram of a sinusoid and mark on it the period T and Amplitude A
This is satisfied by an equation of the form
x
=
A
sin
(
ωt
+
φ0
)
where
A
and
φ0
are constants that are determined by the initial conditions.
Draw a diagram of a sinusoid and mark on it the period T and Amplitude A
φ0
Is an arbitrary phase which shifts the sinusoid.This is also
satisfied by an equation of the form
x
=
A
sin
(
ωt
)
+
B
cos
(
ωt
)
Lets
show this:
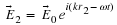 Again
there are two constants determined by the initial conditions
A
and
B
The equation can be rewritten
Again
there are two constants determined by the initial conditions
A
and
B
The equation can be rewritten
 Thus
if
Thus
if
 then
the equation is identical to the SHM equation.
then
the equation is identical to the SHM equation.
So another way to write the equation of Simple Harmonic Motion is
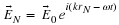 or
or
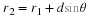
It is also important to remember the relationships between freqency, angular
frequency and period:
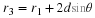
Another solution to the SHM equation is
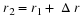 Recall Taylor's expansions of sine and cosine
Recall Taylor's expansions of sine and cosine

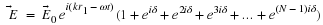 Then
Then

(an alternative way to show this is the following)
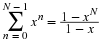
Thus we can write
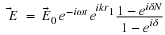 as
as
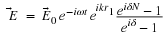
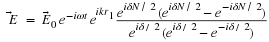
We will use the complex representation a lot, so you need to
become familiar with it. It is used a lot in Optics, Classical and Quantum
Mechanics and Electrical Engineering so it is a good thing to know.
Now for physical systems we are interested in just the real
part so
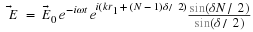 This
will be implicitly understood. In physics we just write
x
=
A
ei
(
ωt
+
φ0
)
One thing that will seem to be confusing is that there are all these different
solutions. They are all just different forms of the same thing. Which form is
used in a particular circumstance is simply a matter of convenience. Some
forms lend themselves to to solutions of certain problems more easily than
others. Also the most convenient form can depend upon the initial conditions.
For example if
x
is at its maximum displacement at time
t
=
0
then a
cos
form may be the most convenient. As a general rule I like using the complex
representation because natural logarithms are so easy to work with. For
example
This
will be implicitly understood. In physics we just write
x
=
A
ei
(
ωt
+
φ0
)
One thing that will seem to be confusing is that there are all these different
solutions. They are all just different forms of the same thing. Which form is
used in a particular circumstance is simply a matter of convenience. Some
forms lend themselves to to solutions of certain problems more easily than
others. Also the most convenient form can depend upon the initial conditions.
For example if
x
is at its maximum displacement at time
t
=
0
then a
cos
form may be the most convenient. As a general rule I like using the complex
representation because natural logarithms are so easy to work with. For
example
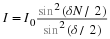
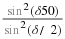
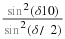 which
is all pretty simple to remember
which
is all pretty simple to remember