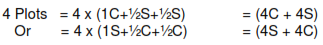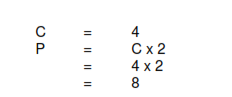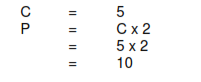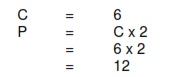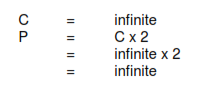TEASER - 08
PLOTS & SUB-PLOTS
A square piece of plot / land (green) with open space and road (brown) on all side is to be divided into many sub-plots (parts). With following conditions,
1) All sub-plots should be equal in size
2) All sub-plots should be equal in shape
3) All sub-plots should have equal accessibility to road and open space present on all sides
Under aforementioned conditions, this piece of land can be divided into how many maximum sub-plots (parts)


SQUARE PLOT WITH ROADS ON ALL SIDES
THE EXPLANATION:
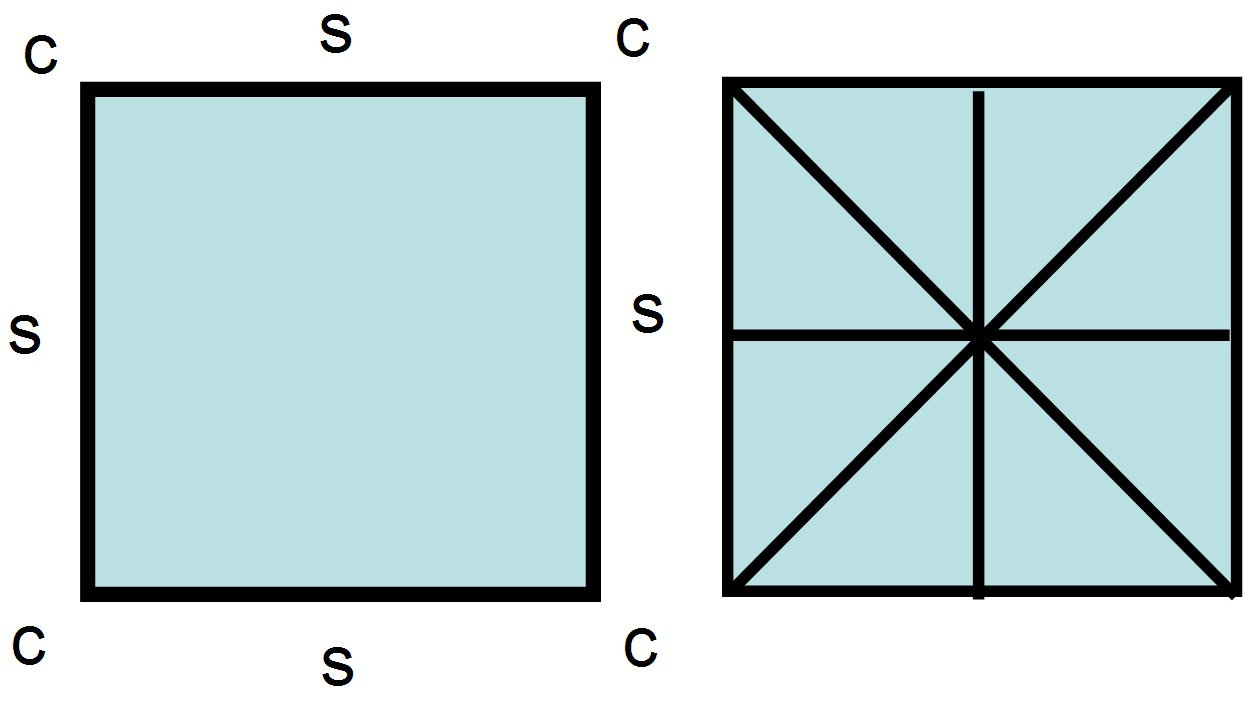
Division of a square plot of land:
The land being an areal quantity, it can have only two dimensions (2D), therefore individual sides or individual corners can be divided 2 times only to make them symmetrical on either side of a line. The square plot of a land has 4 corners (4C) and 4 sides (4S) and each side has fixed length and each corner has fixed angle, hence the sum total of length of sides and angle of corners when divided should remain constant (4C + 4S).
Corners (C) = 4
Sides (S) = 4
SQUARE PLOT WITH 4 SIDES & 4 CORN
(1) When divided into 2 sub-plots:


SQUARE PLOT DIVIDED INTO 2 EQUAL PARTS
(2) When divided into 4 sub-plots:
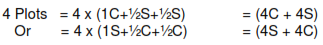

SQUARE PLOT DIVIDED INTO 4 EQUAL PARTS
(3) When divided into 8 sub-plots:
8 Plots = 8 x (½C +½S) = (4C + 4S)
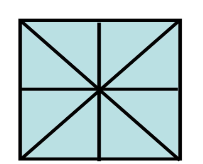
SQUARE PLOT DIVIDED INTO 8 EQUAL PARTS
Keeping in focus the conditions laid down above, it is observed that a square land can be divided into 2, 4 and 8 equitable sub-plots only and cannot be divided into 3, 5, 6, 7, 9 or more number of sub-plots.
The shape of a piece of land can be trigonal, pentagonal, hexagonal, circular and so on.
The sub-divisions or sub-plots are in a way symmetrical divisions and their number is dependant on the shape of a plot. The corners and sides of a square or a hexagonal shaped land have fixed number of corners and sides and are linked together in a definite pattern. To make identical sub-divisions (sub-plots) corners and sides would have to be equally shared without changing their original positions.
The relationship between the number of corners or sides and the maximum possible sub-divisions or sub-plots equal in all respect can be established in following manner:

Square plot (4 sided)
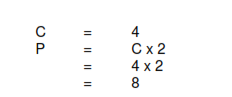
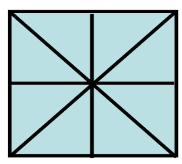
8 EQUAL DIVISIONS
Trigonal plot (3 sided)

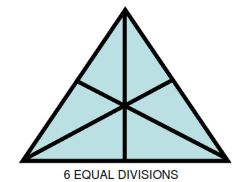
6 EQUAL DIVISIONS
Pentagonal plot (5 sided)
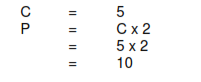

10 EQUAL DIVISIONS
Hexagonal plot (6 sided)
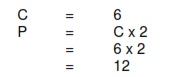
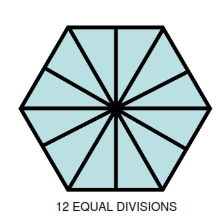
12 EQUAL DIVISIONS
Round plot (infinite sided)
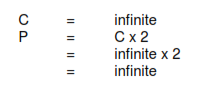

INFINITE EQUAL DIVISIONS
An infinite number of radial rays can be drawn from the center of a circle (round plot) outward. A circle can have any number of sides and corners hence it can be divided into an infinite number of equal parts or sub-plots.
********