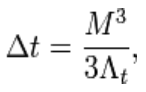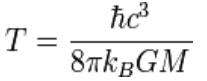Inside a Black Hole
It is impossible to look into a black hole. Hence it becomes necessary to employ mathematics for that purpose. An Event Horizon has no actual hard surface as in the case of planets. It is a theoretical border defined by mathematics. Beyond that border, no radiation of any type can leave the Hole. We do however, want to know what happens on the far side of the event horizon as the very title of this book might suggest. Probably matter beyond that horizon is aggregated into a small core as we know it to be in neutron stars. Yet a neutron star has no centre called a singularity, whereas a black hole is supposed to have such. Because of the extreme density in that singularity, the formulae of Lorentz and Einstein will very likely no longer apply. Mathematics shows that space becomes time and time becomes space.

Since Karl Schwarzschild, the centre of the black hole has acquired the expression Singularity. He calculated that a non-rotating hole contained all of its mass in that centre. (See the chapter "The Previous History").
Fifty years later it became obvious that every Black Hole possessed some spin. Roy Patrick Kerr demonstrated mathematically, that a black hole is a rotating space-time having a Ring singularity in its centre and the core in the form of an oval.


Kerr´s vision of a fast rotating black hole, was that it possesses mass, angular momentum (spin) and perhaps electrical charge, the last not proven. This model found favour until modern times. There are stunning similarities in these characteristics to fundamental particles. Equally, atoms have qualities like mass, angular momentum and electrical charge, with nothing else.
The result of Kerr´s calculations showed that a rotating black hole would impart rotation to anything approaching the event horizon. This means that matter, light and magnetic fields, are forced to adopt the spin, the direction of the rotation and the same angular speed of the black hole itself, a behaviour known as frame dragging, meaning the taking along of any framework to another frame of reference. Kerr arrived at the conclusion that a motionless observer, beside an event horizon is not possible.
The Frame Drag will cause magnetic fields to become twisted and amplified significantly. So-called Alvén waves will be created along the axes of rotation, becoming so immensely strong that at both, poles, matter and all sorts of electromagnetic waves are emitted. This idea is confirmed by calculations in a special branch of mathematics, the so-called Magnetohydrodynamics.

Frame Dragging, creating jets at the poles of a Black Hole. An artist impression (By courtesy of ESO)
The result of all such effects is that matter which is heated in close proximity to the "Kerr Hole" will be ejected from the poles at high speed. Presumably, this will be a kind of high temperature plasma. This polar jet, a phenomenon in astrophysics, created by the mechanism of Magneto-hydrodynamics, may reach millions of lightyears into space. Polar jets are streams of matter emitted along the axis of rotation of a fast rotating star. They seem to play an great role in the cosmic cycle of life. Supernovae caused by collapsing Red Giants, will distribute vast amounts of matter into space. This matter will be re-distributed over great distances when approaching a spinning black hole. Remember, that matter from any supernovae will contain many elements (e.g. carbon, iron, etc etc), the basic modules of new sun systems. Black holes seem to be the essence, not simply the destruction of destroying stars but also the very creation of new ones. This includes planets and complete star systems like ours. The significance of black holes to life seems to be immense.

A black hole is a celestial object with a sudden appearance. It is expected to grow permanently. Will a black hole exist forever? Will it grow perpetually by absorption of any matter randomly approaching too closely? Will it continue "in perpetuum?" For many years, such questions occupied the brilliant mind of Stephen Hawking, the famous British theoretical physicist, cosmologist, author & Professor at the University of Cambridge. Hawking suffers lateral sclerosis (ALS), also referred to in the USA as Lou Gehrig´s. Doctors predicted a short life for him. To overcome his difficulty with speech, he needs the assistance of a computer and speech synthesiser. To this day, the famous Professor Hawking is alive and working on Black Holes. Before 2004 Hawking supported Wheeler‘s "no-hairs theorem" (see page 37). He had a bet with a collegue, John Preskill, who contradicted the theorem. Subsequent calculations carried out by Hawking, had shown that black holes might very well diminish and ultimately disappear by the emission of small amounts of thermal radiation. In 2004, at the Dublin "International Conference on General Relativity and Gravitation" he declared his bet to be lost and conceded that a black hole is not entirely black.

Black holes do have hairs - a metaphor for all kinds of radiation and what Hawking called "information". The wager was, showing the British sense of humour, an encyclopedia containing much information on what would survive when succumbing to a black hole. Hawking, in parodying Einstein said: "God will play dice but sometimes the dies cannot be seen!"

Hawking lost his bet: the wager was an encyclopedia
What bothers Hawking about black holes is that they oppose two earlier fundamental laws; the thermodynamic equilibrium and human common sense, both of which say that nothing exists forever. Physics clearly states that in any isolated system (The Universe) the energy in total will remain constant, in accordance with the laws of thermodynamics. Matter would eventually disappear from the Universe if there were no mechanism to allow some to escape from the black hole. Hawking established that a certain amount of radiation can exit from black holes. This kind of radiation was later given his name: Hawking radiation. If Hawking's theory of black hole radiation is correct, then black holes can be expected to shrink and evaporate over time because of the leakage of mass via the emission of photons and other particles.
As early as 1970, Hawking was fascinated with Black Holes, created since the birth of The Universe in the Big Bang. His calculations also resulted in tiny Black Holes, the so called primordial Black Holes. Together with other kinds of Black Holes, identified today, the entire family was assembled - in ascending order of size:

In September 2010, a signal that is closely related to Black Hole Hawking radiation was claimed to have been observed in an experiment. The results however remain unverified and debatable.
One of the most important contributions of Hawking was: "The Black Hole Information Loss Problem". Information here, means matter, energy and the laws describing them. Hawking Radiation reduces the mass and the energy of the black hole and consequently it may lose more mass than gained through accretion. As a consequence it will shrink until its mass reaches zero, wherupon it will disappear. This is the clear outcome of Hawking Radiation. The question is how long does it take until it disappears? If the time span is very great – and it does appear that the black hole in the centre of our Milky Way has existed for a long time period – then Hawking Radiation has no effect on the destiny of The Universe.
As it has been determined that a black hole is able to shrink by permanently losing energy through Hawking Radiation, it will, as a consequence be gone after a certain period of time. This period Δt will be calculated through the Hawking equation by:
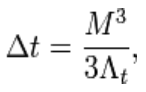
This equation shows how the life-time of a black hole quite depends upon its mass M. One can say "the greater the mass the longer will be the life time". Conversely, the life of smaller black holes will shorter. The formula will be valid in the case of a black hole which has no chance to add further matter. This could possibly be due to an absence of matter in close proximity. Hawking also tried to calculate temperatures inside a black hole. Surprisingly, temperatures T are inversely proportional to the size of a hole:
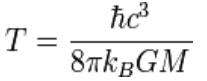
The numerator contains the so-called Planck´s quantum of action h and as usual the speed of light c. The Denominator contains the constant of Boltzmann k the gravitational constant G as well as the mass of the black hole M. Doing the calculation gives a surprising result: the temperature of a black hole drops as its mass increases. Big black holes have inside temperatures similar to those in a living room.
In June 2013 the headline of a press agency (DPA) in a German newspaper was:
"Black Holes Raise Dust":
Usually, dust close to a big black hole like the galaxy NGC3783, displays a temperature from 700 to 1000 degrees C. The "Very Large Telescope" of ESO has measured the core as ‘having a temperature not unlike any living room.‘

This image, taken by the Mexican University UNAM shows the bright Halo around the Black Hole NGC3783 (By courtesy of UNAM)
This headline impressively confirmed Hawking ´s formula. With the use of modern technology, it can now be measured and confirmed what Hawking et al. had supposed, many years earlier.

2012 Joe Polchinski, working at the University of California set off a controversial debate. His argument: Everywhere in the Universe, new pairs of particles and antiparticles come into existence, interacting with each other. If that happens close to the event horizon, it might be that one part of the pair were captured by the black hole but not so the partner. In that case the remaining particle would appear to us in the form of visible radiation. The rest would be captured by the black hole in the form of negative energy, diminishing it and eventually causing it to disappear. It would evaporate. Hawking´s work was confirmed.
Polchinski concluded that the interlacing of particles would be stopped under the release of great amounts of energy in the form of X-rays and Gamma-rays. The event horizon would destroy everything close to it, in a ring of fire. If Polchinski were right, space travel by the use of black holes and worm holes, into parallel universe would be impossible. (see the previous chapter "Flight to a Black Hole")