The kinetic energy the person has upon reaching the floor is the amount of potential energy lost by falling through height h :
(7.30)
KE = −ΔPEg = − mgh,
The distance d that the person’s knees bend is much smaller than the height h of the fall, so the additional change in gravitational potential
energy during the knee bend is ignored.
The work W done by the floor on the person stops the person and brings the person’s kinetic energy to zero:
W
(7.31)
= −KE = mgh.
Combining this equation with the expression for W gives
(7.32)
− Fd = mgh.
Recalling that h is negative because the person fell down, the force on the knee joints is given by
⎛
⎛
(7.33)
F = − mgh
⎝60.0 kg⎞⎠⎝9.80 m/s2⎞⎠(−3.00 m)
d = −
= 3.53×105 N.
5.00×10−3 m
Discussion
Such a large force (500 times more than the person’s weight) over the short impact time is enough to break bones. A much better way to cushion
the shock is by bending the legs or rolling on the ground, increasing the time over which the force acts. A bending motion of 0.5 m this way yields
a force 100 times smaller than in the example. A kangaroo's hopping shows this method in action. The kangaroo is the only large animal to use
hopping for locomotion, but the shock in hopping is cushioned by the bending of its hind legs in each jump.(See Figure 7.7.)

230 CHAPTER 7 | WORK, ENERGY, AND ENERGY RESOURCES
Figure 7.7 The work done by the ground upon the kangaroo reduces its kinetic energy to zero as it lands. However, by applying the force of the ground on the hind legs over a
longer distance, the impact on the bones is reduced. (credit: Chris Samuel, Flickr)
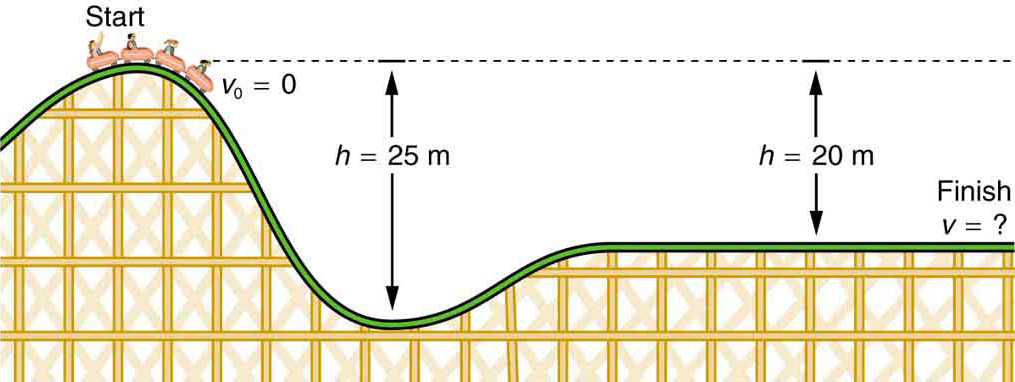
Example 7.7 Finding the Speed of a Roller Coaster from its Height
(a) What is the final speed of the roller coaster shown in Figure 7.8 if it starts from rest at the top of the 20.0 m hill and work done by frictional forces is negligible? (b) What is its final speed (again assuming negligible friction) if its initial speed is 5.00 m/s?
Figure 7.8 The speed of a roller coaster increases as gravity pulls it downhill and is greatest at its lowest point. Viewed in terms of energy, the roller-coaster-Earth
system’s gravitational potential energy is converted to kinetic energy. If work done by friction is negligible, all ΔPEg is converted to KE .
Strategy
The roller coaster loses potential energy as it goes downhill. We neglect friction, so that the remaining force exerted by the track is the normal
force, which is perpendicular to the direction of motion and does no work. The net work on the roller coaster is then done by gravity alone. The
loss of gravitational potential energy from moving downward through a distance h equals the gain in kinetic energy. This can be written in
equation form as −ΔPEg = ΔKE . Using the equations for PEg and KE , we can solve for the final speed v , which is the desired quantity.
Solution for (a)
Here the initial kinetic energy is zero, so that ΔKE = 12 mv 2 . The equation for change in potential energy states that ΔPEg = mgh . Since h
is negative in this case, we will rewrite this as ΔPEg = − mg ∣ h ∣ to show the minus sign clearly. Thus,
(7.34)
−ΔPEg = ΔKE
becomes
(7.35)
mg ∣ h ∣ = 12 mv 2.
Solving for v , we find that mass cancels and that
(7.36)
v = 2 g ∣ h ∣ .

CHAPTER 7 | WORK, ENERGY, AND ENERGY RESOURCES 231
Substituting known values,
(7.37)
v = 2⎛⎝9.80 m/s2⎞⎠(20.0 m)
= 19.8 m/s.
Solution for (b)
Again − ΔPE
2
g = ΔKE . In this case there is initial kinetic energy, so ΔKE = 12 mv 2 − 12 mv 0 . Thus,
2
(7.38)
mg ∣ h ∣ = 12 mv 2 − 12 mv 0 .
Rearranging gives
2
(7.39)
12 mv 2 = mg ∣ h ∣ + 12 mv 0 .
This means that the final kinetic energy is the sum of the initial kinetic energy and the gravitational potential energy. Mass again cancels, and
(7.40)
v = 2 g ∣ h ∣ + v 2
0 .
This equation is very similar to the kinematics equation v = v 2
0 + 2 ad , but it is more general—the kinematics equation is valid only for
constant acceleration, whereas our equation above is valid for any path regardless of whether the object moves with a constant acceleration.
Now, substituting known values gives
(7.41)
v = 2(9.80 m/s2)(20.0 m) + (5.00 m/s)2
= 20.4 m/s.
Discussion and Implications
First, note that mass cancels. This is quite consistent with observations made in Falling Objects that all objects fall at the same rate if friction is negligible. Second, only the speed of the roller coaster is considered; there is no information about its direction at any point. This reveals another
general truth. When friction is negligible, the speed of a falling body depends only on its initial speed and height, and not on its mass or the path
taken. For example, the roller coaster will have the same final speed whether it falls 20.0 m straight down or takes a more complicated path like
the one in the figure. Third, and perhaps unexpectedly, the final speed in part (b) is greater than in part (a), but by far less than 5.00 m/s. Finally,
note that speed can be found at any height along the way by simply using the appropriate value of h at the point of interest.
We have seen that work done by or against the gravitational force depends only on the starting and ending points, and not on the path between,
allowing us to define the simplifying concept of gravitational potential energy. We can do the same thing for a few other forces, and we will see that
this leads to a formal definition of the law of conservation of energy.
Making Connections: Take-Home Investigation—Converting Potential to Kinetic Energy
One can study the conversion of gravitational potential energy into kinetic energy in this experiment. On a smooth, level surface, use a ruler of
the kind that has a groove running along its length and a book to make an incline (see Figure 7.9). Place a marble at the 10-cm position on the
ruler and let it roll down the ruler. When it hits the level surface, measure the time it takes to roll one meter. Now place the marble at the 20-cm
and the 30-cm positions and again measure the times it takes to roll 1 m on the level surface. Find the velocity of the marble on the level surface
for all three positions. Plot velocity squared versus the distance traveled by the marble. What is the shape of each plot? If the shape is a straight
line, the plot shows that the marble’s kinetic energy at the bottom is proportional to its potential energy at the release point.
Figure 7.9 A marble rolls down a ruler, and its speed on the level surface is measured.
7.4 Conservative Forces and Potential Energy
Potential Energy and Conservative Forces
Work is done by a force, and some forces, such as weight, have special characteristics. A conservative force is one, like the gravitational force, for
which work done by or against it depends only on the starting and ending points of a motion and not on the path taken. We can define a potential
energy (PE) for any conservative force, just as we did for the gravitational force. For example, when you wind up a toy, an egg timer, or an old-
232 CHAPTER 7 | WORK, ENERGY, AND ENERGY RESOURCES
fashioned watch, you do work against its spring and store energy in it. (We treat these springs as ideal, in that we assume there is no friction and no
production of thermal energy.) This stored energy is recoverable as work, and it is useful to think of it as potential energy contained in the spring.
Indeed, the reason that the spring has this characteristic is that its force is conservative. That is, a conservative force results in stored or potential
energy. Gravitational potential energy is one example, as is the energy stored in a spring. We will also see how conservative forces are related to the
conservation of energy.
Potential Energy and Conservative Forces
Potential energy is the energy a system has due to position, shape, or configuration. It is stored energy that is completely recoverable.
A conservative force is one for which work done by or against it depends only on the starting and ending points of a motion and not on the path
taken.
We can define a potential energy (PE) for any conservative force. The work done against a conservative force to reach a final configuration
depends on the configuration, not the path followed, and is the potential energy added.
Potential Energy of a Spring
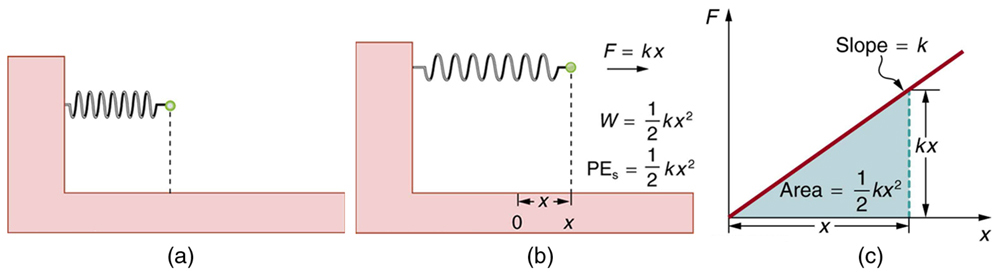
First, let us obtain an expression for the potential energy stored in a spring ( PEs ). We calculate the work done to stretch or compress a spring that
obeys Hooke’s law. (Hooke’s law was examined in Elasticity: Stress and Strain, and states that the magnitude of force F on the spring and the resulting deformation Δ L are proportional, F = kΔ L .) (See Figure 7.10.) For our spring, we will replace Δ L (the amount of deformation produced by a force F ) by the distance x that the spring is stretched or compressed along its length. So the force needed to stretch the spring has
magnitude F = kx , where k is the spring’s force constant. The force increases linearly from 0 at the start to kx in the fully stretched position. The
⎞
average force is kx / 2 . Thus the work done in stretching or compressing the spring is W
kx
s = Fd = ⎛⎝ 2 ⎠ x = 12 kx 2 . Alternatively, we noted in
Kinetic Energy and the Work-Energy Theorem that the area under a graph of F vs. x is the work done by the force. In Figure 7.10(c) we see
that this area is also 1
2 kx 2 . We therefore define the potential energy of a spring, PEs , to be
(7.42)
PEs = 12 kx 2,
where k is the spring’s force constant and x is the displacement from its undeformed position. The potential energy represents the work done on
the spring and the energy stored in it as a result of stretching or compressing it a distance x . The potential energy of the spring PEs does not
depend on the path taken; it depends only on the stretch or squeeze x in the final configuration.
Figure 7.10 (a) An undeformed spring has no PEs stored in it. (b) The force needed to stretch (or compress) the spring a distance x has a magnitude F = kx , and the 1
work done to stretch (or compress) it is 2 kx 2 . Because the force is conservative, this work is stored as potential energy (PEs) in the spring, and it can be fully recovered.
1
1
(c) A graph of F vs. x has a slope of k , and the area under the graph is 2 kx 2 . Thus the work done or potential energy stored is 2 kx 2 .
The equation PEs = 12 kx 2 has general validity beyond the special case for which it was derived. Potential energy can be stored in any elastic
medium by deforming it. Indeed, the general definition of potential energy is energy due to position, shape, or configuration. For shape or position
deformations, stored energy is PEs = 12 kx 2 , where k is the force constant of the particular system and x is its deformation. Another example is
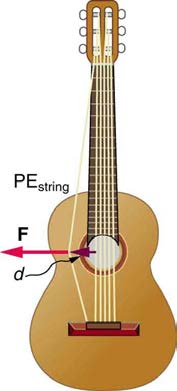
seen in Figure 7.11 for a guitar string.
CHAPTER 7 | WORK, ENERGY, AND ENERGY RESOURCES 233
Figure 7.11 Work is done to deform the guitar string, giving it potential energy. When released, the potential energy is converted to kinetic energy and back to potential as the string oscillates back and forth. A very small fraction is dissipated as sound energy, slowly removing energy from the string.
Conservation of Mechanical Energy
Let us now consider what form the work-energy theorem takes when only conservative forces are involved. This will lead us to the conservation of
energy principle. The work-energy theorem states that the net work done by all forces acting on a system equals its change in kinetic energy. In
equation form, this is
2
(7.43)
W net = 12 mv 2 − 12 mv 0 = ΔKE.
If only conservative forces act, then
W
(7.44)
net = W c,
where W c is the total work done by all conservative forces. Thus,
W
(7.45)
c = ΔKE.
Now, if the conservative force, such as the gravitational force or a spring force, does work, the system loses potential energy. That is, W c = −ΔPE .
Therefore,
(7.46)
−ΔPE = ΔKE
or
(7.47)
ΔKE + ΔPE = 0.
This equation means that the total kinetic and potential energy is constant for any process involving only conservative forces. That is,
(7.48)
KE + PE = constant ⎫
or
⎬(conservative forces only),
KEi + PEi = KEf + PEf⎭
where i and f denote initial and final values. This equation is a form of the work-energy theorem for conservative forces; it is known as the
conservation of mechanical energy principle. Remember that this applies to the extent that all the forces are conservative, so that friction is
negligible. The total kinetic plus potential energy of a system is defined to be its mechanical energy, (KE + PE) . In a system that experiences only
conservative forces, there is a potential energy associated with each force, and the energy only changes form between KE and the various types of
PE , with the total energy remaining constant.
Example 7.8 Using Conservation of Mechanical Energy to Calculate the Speed of a Toy Car
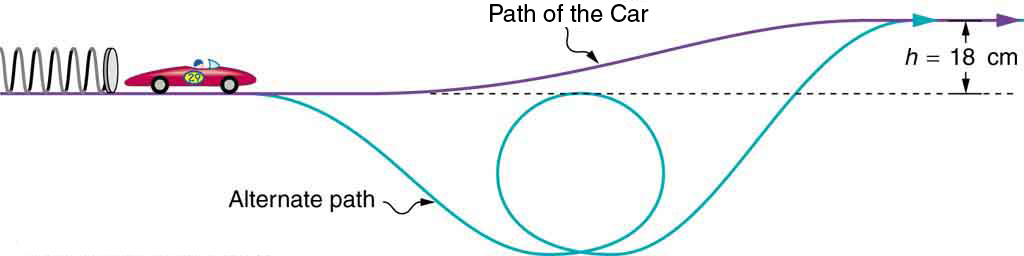
A 0.100-kg toy car is propelled by a compressed spring, as shown in Figure 7.12. The car follows a track that rises 0.180 m above the starting
point. The spring is compressed 4.00 cm and has a force constant of 250.0 N/m. Assuming work done by friction to be negligible, find (a) how
fast the car is going before it starts up the slope and (b) how fast it is going at the top of the slope.
234 CHAPTER 7 | WORK, ENERGY, AND ENERGY RESOURCES
Figure 7.12 A toy car is pushed by a compressed spring and coasts up a slope. Assuming negligible friction, the potential energy in the spring is first completely
converted to kinetic energy, and then to a combination of kinetic and gravitational potential energy as the car rises. The details of the path are unimportant because all
forces are conservative—the car would have the same final speed if it took the alternate path shown.
Strategy
The spring force and the gravitational force are conservative forces, so conservation of mechanical energy can be used. Thus,
(7.49)
KEi+PEi = KEf + PEf
or
2
2
2
2
(7.50)
12 mv i + mgh i+ 12 kx = 1 + mgh
,
i
2 mv f
f + 12 kx f
where h is the height (vertical position) and x is the compression of the spring. This general statement looks complex but becomes much
simpler when we start considering specific situations. First, we must identify the initial and final conditions in a problem; then, we enter them into
the last equation to solve for an unknown.
Solution for (a)
This part of the problem is limited to conditions just before the car is released and just after it leaves the spring. Take the initial height to be zero,
so that both h i and h f are zero. Furthermore, the initial speed v i is zero and the final compression of the spring x f is zero, and so several
terms in the conservation of mechanical energy equation are zero and it simplifies to
2
2
(7.51)
12 kx i = 12 mv f .
In other words, the initial potential energy in the spring is converted completely to kinetic energy in the absence of friction. Solving for the final
speed and entering known values yields
(7.52)
v f = kmx i
= 250.0 N/m
0.100 kg (0.0400 m)
= 2.00 m/s.
Solution for (b)
One method of finding the speed at the top of the slope is to consider conditions just before the car is released and just after it reaches the top of
the slope, completely ignoring everything in between. Doing the same type of analysis to find which terms are zero, the conservation of
mechanical energy becomes
2
2
(7.53)
12 kx i = 1 2 mv f + mgh f.
This form of the equation means that the spring’s initial potential energy is converted partly to gravitational potential energy and partly to kinetic
energy. The final speed at the top of the slope will be less than at the bottom. Solving for v f and substituting known values gives
(7.54)
2
v f = kx i m − 2 gh f
= ⎛250.0 N/m⎞
⎝ 0.100 kg ⎠(0.0400 m)2 − 2(9.80 m/s2)(0.180 m)
= 0.687 m/s.
Discussion
Another way to solve this problem is to realize that the car’s kinetic energy before it goes up the slope is converted partly to potential
energy—that is, to take the final conditions in part (a) to be the initial conditions in part (b).
Note that, for conservative forces, we do not directly calculate the work they do; rather, we consider their effects through their corresponding potential
energies, just as we did in Example 7.8. Note also that we do not consider details of the path taken—only the starting and ending points are
important (as long as the path is not impossible). This assumption is usually a tremendous simplification, because the path may be complicated and
forces may vary along the way.

CHAPTER 7 | WORK, ENERGY, AND ENERGY RESOURCES 235
PhET Explorations: Energy Skate Park
Learn about conservation of energy with a skater dude! Build tracks, ramps and jumps for the skater and view the kinetic energy, potential
energy and friction as he moves. You can also take the skater to different planets or even space!
Figure 7.13 Energy Skate Park (http://cnx.org/content/m42149/1.3/energy-skate-park_en.jar)
7.5 Nonconservative Forces
Nonconservative Forces and Friction
Forces are either conservative or nonconservative. Conservative forces were discussed in Conservative Forces and Potential Energy. A
nonconservative force is one for which work depends on the path taken. Friction is a good example of a nonconservative force. As illustrated in
Figure 7.14, work done against friction depends on the length of the path between the starting and ending points. Because of this dependence on
path, there is no potential energy associated with nonconservative forces. An important characteristic is that the work done by a nonconservative
force adds or removes mechanical energy from a system. Friction, for example, creates thermal energy that dissipates, removing energy from the
system. Furthermore, even if the thermal energy is retained or captured, it cannot be fully converted back to work, so it is lost or not recoverable in
that sense as well.
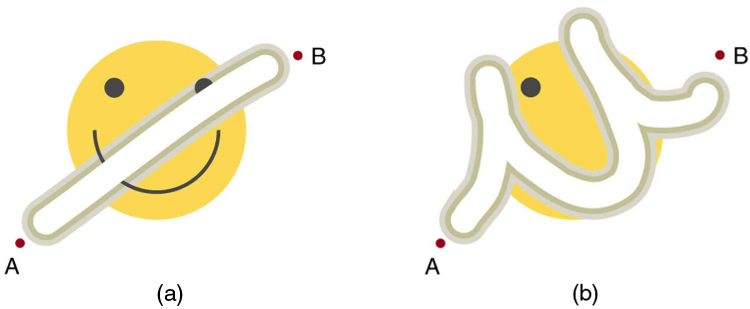
Figure 7.14 The amount of the happy face erased depends on the path taken by the eraser between points A and B, as does the work done against friction. Less work is done
and less of the face is erased for the path in (a) than for the path in (b). The force here is friction, and most of the work goes into thermal energy that subsequently leaves the
system (the happy face plus the eraser). The energy expended cannot be fully recovered.
How Nonconservative Forces Affect Mechanical Energy
Mechanical energy may not be conserved when nonconservative forces act. For example, when a car is brought to a stop by friction on level ground,
it loses kinetic energy, which is dissipated as thermal energy, reducing its mechanical energy. Figure 7.15 compares the effects of conservative and nonconservative forces. We often choose to understand simpler systems such as that described in Figure 7.15(a) first before studying more
complicated systems as in Figure 7.15(b).
236 CHAPTER 7 | WORK, ENERGY, AND ENERGY RESOURCES
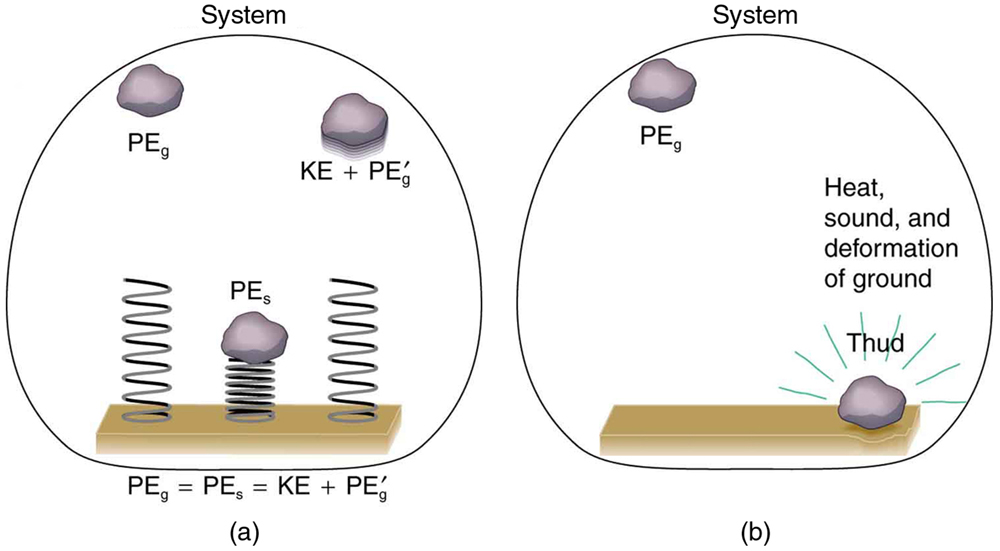
Figure 7.15 Comparison of the effects of conservative and nonconservative forces on the mechanical energy of a system. (a) A system with only conservative forces. When a
rock is dropped onto a spring, its mechanical energy remains constant (neglecting air resistance) because the force in the spring is conservative. The spring can propel the
rock back to its original height, where it once again has only potential energy due to gravity. (b) A system with nonconservative forces. When the same rock is dropped onto the
ground, it is stopped by nonconservative forces that dissipate its mechanical energy as thermal energy, sound, and surface distortion. The rock has lost mechanical energy.
How the Work-Energy Theorem Applies
Now let us consider what form the work-energy theorem takes when both conservative and nonconservative forces act. We will see that the work
done by nonconservative forces equals the change in the mechanical energy of a system. As noted in Kinetic Energy and the Work-Energy
Theorem, the work-energy theorem states that the net work on a system equals the change in its kinetic energy, or













