α
= 0 − 220 rad/s
−300 rad/s2 = 0.733 s.
Discussion
Note that care must be taken with the signs that indicate the directions of various quantities. Also, note that the time to stop the reel is fairly small
because the acceleration is rather large. Fishing lines sometimes snap because of the accelerations involved, and fishermen often let the fish
swim for a while before applying brakes on the reel. A tired fish will be slower, requiring a smaller acceleration.
Example 10.5 Calculating the Slow Acceleration of Trains and Their Wheels
Large freight trains accelerate very slowly. Suppose one such train accelerates from rest, giving its 0.350-m-radius wheels an angular
acceleration of 0.250 rad/s2 . After the wheels have made 200 revolutions (assume no slippage): (a) How far has the train moved down the
track? (b) What are the final angular velocity of the wheels and the linear velocity of the train?
Strategy
In part (a), we are asked to find x , and in (b) we are asked to find ω and v . We are given the number of revolutions θ , the radius of the
wheels r , and the angular acceleration α .
Solution for (a)
The distance x is very easily found from the relationship between distance and rotation angle:
CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM 325
(10.30)
θ = xr.
Solving this equation for x yields
x
(10.31)
= rθ.
Before using this equation, we must convert the number of revolutions into radians, because we are dealing with a relationship between linear
and rotational quantities:
(10.32)
θ = (200 rev)2π rad
1 rev = 1257 rad.
Now we can substitute the known values into x = rθ to find the distance the train moved down the track:
x
(10.33)
= rθ = (0.350 m)(1257 rad) = 440 m.
Solution for (b)
We cannot use any equation that incorporates t to find ω , because the equation would have at least two unknown values. The equation
ω 2 = ω 2
0 + 2 αθ will work, because we know the values for all variables except ω :
2
(10.34)
ω 2 = ω 0 + 2 αθ
Taking the square root of this equation and entering the known values gives
1 / 2
(10.35)
ω = ⎡⎣0 + 2(0.250 rad/s2)(1257 rad)⎤⎦
= 25.1 rad/s.
We can find the linear velocity of the train, v , through its relationship to ω :
v
(10.36)
= rω = (0.350 m)(25.1 rad/s) = 8.77 m/s.
Discussion
The distance traveled is fairly large and the final velocity is fairly slow (just under 32 km/h).
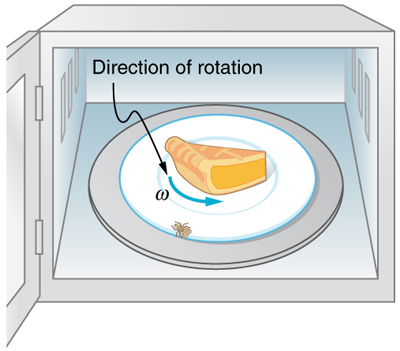
There is translational motion even for something spinning in place, as the following example illustrates. Figure 10.9 shows a fly on the edge of a
rotating microwave oven plate. The example below calculates the total distance it travels.
Figure 10.9 The image shows a microwave plate. The fly makes revolutions while the food is heated (along with the fly).
Example 10.6 Calculating the Distance Traveled by a Fly on the Edge of a Microwave Oven Plate
A person decides to use a microwave oven to reheat some lunch. In the process, a fly accidentally flies into the microwave and lands on the
outer edge of the rotating plate and remains there. If the plate has a radius of 0.15 m and rotates at 6.0 rpm, calculate the total distance traveled
by the fly during a 2.0-min cooking period. (Ignore the start-up and slow-down times.)
Strategy
First, find the total number of revolutions θ , and then the linear distance x traveled. θ = ω¯ t can be used to find θ because ω- is given to be 6.0 rpm.
Solution
Entering known values into θ = ω¯ t gives
(10.37)
θ = ω- t = ⎛⎝6.0 rpm⎞⎠(2.0 min) = 12 rev.
326 CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM
As always, it is necessary to convert revolutions to radians before calculating a linear quantity like x from an angular quantity like θ :
⎞
(10.38)
θ = (12 rev)⎛2 π rad
⎝ 1 rev ⎠ = 75.4 rad.
Now, using the relationship between x and θ , we can determine the distance traveled:
x
(10.39)
= rθ = (0.15 m)(75.4 rad) = 11 m.
Discussion
Quite a trip (if it survives)! Note that this distance is the total distance traveled by the fly. Displacement is actually zero for complete revolutions
because they bring the fly back to its original position. The distinction between total distance traveled and displacement was first noted in One-
Dimensional Kinematics.
Check Your Understanding
Rotational kinematics has many useful relationships, often expressed in equation form. Are these relationships laws of physics or are they simply
descriptive? (Hint: the same question applies to linear kinematics.)
Solution
Rotational kinematics (just like linear kinematics) is descriptive and does not represent laws of nature. With kinematics, we can describe many
things to great precision but kinematics does not consider causes. For example, a large angular acceleration describes a very rapid change in
angular velocity without any consideration of its cause.
10.3 Dynamics of Rotational Motion: Rotational Inertia
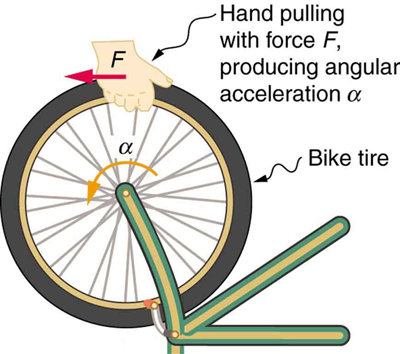
If you have ever spun a bike wheel or pushed a merry-go-round, you know that force is needed to change angular velocity as seen in Figure 10.10.
In fact, your intuition is reliable in predicting many of the factors that are involved. For example, we know that a door opens slowly if we push too
close to its hinges. Furthermore, we know that the more massive the door, the more slowly it opens. The first example implies that the farther the
force is applied from the pivot, the greater the angular acceleration; another implication is that angular acceleration is inversely proportional to mass.
These relationships should seem very similar to the familiar relationships among force, mass, and acceleration embodied in Newton’s second law of
motion. There are, in fact, precise rotational analogs to both force and mass.
Figure 10.10 Force is required to spin the bike wheel. The greater the force, the greater the angular acceleration produced. The more massive the wheel, the smaller the
angular acceleration. If you push on a spoke closer to the axle, the angular acceleration will be smaller.
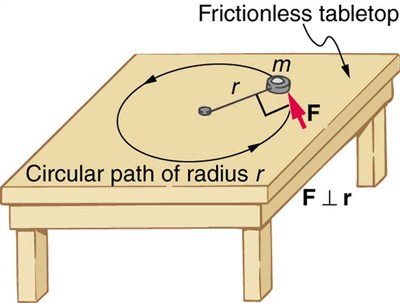
To develop the precise relationship among force, mass, radius, and angular acceleration, consider what happens if we exert a force F on a point
mass m that is at a distance r from a pivot point, as shown in Figure 10.11. Because the force is perpendicular to r , an acceleration a = F
m is
obtained in the direction of F . We can rearrange this equation such that F = ma and then look for ways to relate this expression to expressions for
rotational quantities. We note that a = rα , and we substitute this expression into F = ma , yielding
F
(10.40)
= mrα.
Recall that torque is the turning effectiveness of a force. In this case, because F is perpendicular to r , torque is simply τ = Fr . So, if we multiply both sides of the equation above by r , we get torque on the left-hand side. That is,
(10.41)
rF = mr 2 α
or
(10.42)
τ = mr 2α.
This last equation is the rotational analog of Newton’s second law ( F = ma ), where torque is analogous to force, angular acceleration is analogous
to translational acceleration, and mr 2 is analogous to mass (or inertia). The quantity mr 2 is called the rotational inertia or moment of inertia of a
point mass m a distance r from the center of rotation.
CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM 327
Figure 10.11 An object is supported by a horizontal frictionless table and is attached to a pivot point by a cord that supplies centripetal force. A force F is applied to the object perpendicular to the radius r , causing it to accelerate about the pivot point. The force is kept perpendicular to r .
Making Connections: Rotational Motion Dynamics
Dynamics for rotational motion is completely analogous to linear or translational dynamics. Dynamics is concerned with force and mass and their
effects on motion. For rotational motion, we will find direct analogs to force and mass that behave just as we would expect from our earlier
experiences.
Rotational Inertia and Moment of Inertia
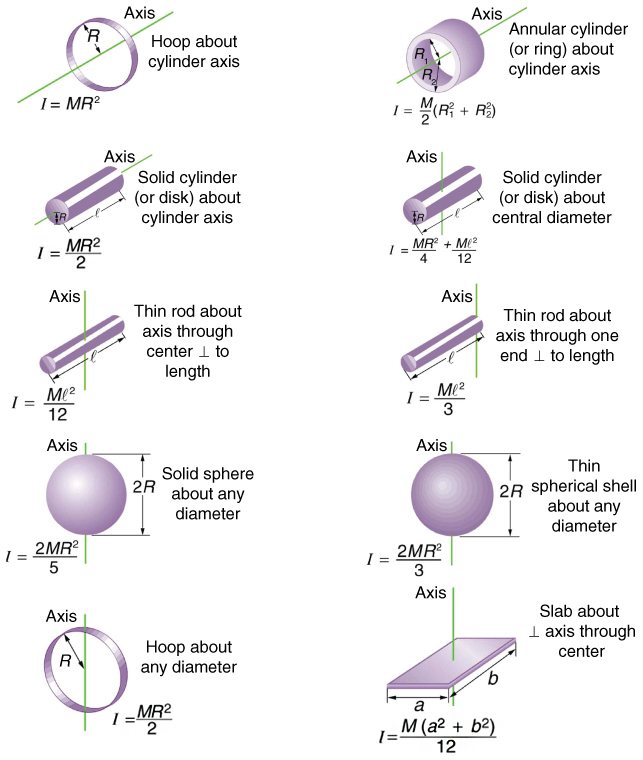
Before we can consider the rotation of anything other than a point mass like the one in Figure 10.11, we must extend the idea of rotational inertia to all types of objects. To expand our concept of rotational inertia, we define the moment of inertia I of an object to be the sum of mr 2 for all the
point masses of which it is composed. That is, I = ∑ mr 2 . Here I is analogous to m in translational motion. Because of the distance r , the moment of inertia for any object depends on the chosen axis. Actually, calculating I is beyond the scope of this text except for one simple case—that
of a hoop, which has all its mass at the same distance from its axis. A hoop’s moment of inertia around its axis is therefore MR 2 , where M is its
total mass and R its radius. (We use M and R for an entire object to distinguish them from m and r for point masses.) In all other cases, we must consult Figure 10.12 (note that the table is piece of artwork that has shapes as well as formulae) for formulas for I that have been derived from integration over the continuous body. Note that I has units of mass multiplied by distance squared ( kg ⋅ m2 ), as we might expect from its
definition.
The general relationship among torque, moment of inertia, and angular acceleration is
(10.43)
net τ = Iα
or
(10.44)
α = net τ
I ,
where net τ is the total torque from all forces relative to a chosen axis. For simplicity, we will only consider torques exerted by forces in the plane of
the rotation. Such torques are either positive or negative and add like ordinary numbers. The relationship in τ = Iα, α = net τ
I is the rotational
analog to Newton’s second law and is very generally applicable. This equation is actually valid for any torque, applied to any object, relative to any
axis.
As we might expect, the larger the torque is, the larger the angular acceleration is. For example, the harder a child pushes on a merry-go-round, the
faster it accelerates. Furthermore, the more massive a merry-go-round, the slower it accelerates for the same torque. The basic relationship between
moment of inertia and angular acceleration is that the larger the moment of inertia, the smaller is the angular acceleration. But there is an additional
twist. The moment of inertia depends not only on the mass of an object, but also on its distribution of mass relative to the axis around which it rotates.
For example, it will be much easier to accelerate a merry-go-round full of children if they stand close to its axis than if they all stand at the outer edge.
The mass is the same in both cases; but the moment of inertia is much larger when the children are at the edge.
Take-Home Experiment
Cut out a circle that has about a 10 cm radius from stiff cardboard. Near the edge of the circle, write numbers 1 to 12 like hours on a clock face.
Position the circle so that it can rotate freely about a horizontal axis through its center, like a wheel. (You could loosely nail the circle to a wall.)
Hold the circle stationary and with the number 12 positioned at the top, attach a lump of blue putty (sticky material used for fixing posters to
walls) at the number 3. How large does the lump need to be to just rotate the circle? Describe how you can change the moment of inertia of the
circle. How does this change affect the amount of blue putty needed at the number 3 to just rotate the circle? Change the circle’s moment of
inertia and then try rotating the circle by using different amounts of blue putty. Repeat this process several times.
Problem-Solving Strategy for Rotational Dynamics
1. Examine the situation to determine that torque and mass are involved in the rotation. Draw a careful sketch of the situation.
2. Determine the system of interest.
3. Draw a free body diagram. That is, draw and label all external forces acting on the system of interest.

328 CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM
4. Apply net τ = Iα, α = net τ
I , the rotational equivalent of Newton’s second law, to solve the problem. Care must be taken to use the
correct moment of inertia and to consider the torque about the point of rotation.
5. As always, check the solution to see if it is reasonable.
Making Connections
In statics, the net torque is zero, and there is no angular acceleration. In rotational motion, net torque is the cause of angular acceleration,
exactly as in Newton’s second law of motion for rotation.
Figure 10.12 Some rotational inertias.
Example 10.7 Calculating the Effect of Mass Distribution on a Merry-Go-Round
Consider the father pushing a playground merry-go-round in Figure 10.13. He exerts a force of 250 N at the edge of the 50.0-kg merry-go-round,
which has a 1.50 m radius. Calculate the angular acceleration produced (a) when no one is on the merry-go-round and (b) when an 18.0-kg child
sits 1.25 m away from the center. Consider the merry-go-round itself to be a uniform disk with negligible retarding friction.
Figure 10.13 A father pushes a playground merry-go-round at its edge and perpendicular to its radius to achieve maximum torque.
CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM 329
Strategy
Angular acceleration is given directly by the expression α = net τ
I :
(10.45)
α = τI.
To solve for α , we must first calculate the torque τ (which is the same in both cases) and moment of inertia I (which is greater in the second
case). To find the torque, we note that the applied force is perpendicular to the radius and friction is negligible, so that
(10.46)
τ = rF sin θ = (1.50 m)(250 N) = 375 N ⋅ m.
Solution for (a)
The moment of inertia of a solid disk about this axis is given in Figure 10.12 to be
(10.47)
12 MR 2,
where M = 50.0 kg and R = 1.50 m , so that
(10.48)
I = (0.500)(50.0 kg)(1.50 m)2 = 56.25 kg ⋅ m2.
Now, after we substitute the known values, we find the angular acceleration to be
(10.49)
α = τI = 375 N ⋅ m
56.25 kg ⋅ m2 = 6.67rad
s2 .
Solution for (b)
We expect the angular acceleration for the system to be less in this part, because the moment of inertia is greater when the child is on the merry-
go-round. To find the total moment of inertia I , we first find the child’s moment of inertia I c by considering the child to be equivalent to a point
mass at a distance of 1.25 m from the axis. Then,
(10.50)
I c = MR 2 = (18.0 kg)(1.25 m)2 = 28.13 kg ⋅ m2.
The total moment of inertia is the sum of moments of inertia of the merry-go-round and the child (about the same axis). To justify this sum to
yourself, examine the definition of I :
(10.51)
I = 28.13 kg ⋅ m2 + 56.25 kg ⋅ m2 = 84.38 kg ⋅ m2.
Substituting known values into the equation for α gives
(10.52)
α = τ I = 375 N ⋅ m
84.38 kg ⋅ m2 = 4.44rad
s2 .
Discussion
The angular acceleration is less when the child is on the merry-go-round than when the merry-go-round is empty, as expected. The angular
accelerations found are quite large, partly due to the fact that friction was considered to be negligible. If, for example, the father kept pushing
perpendicularly for 2.00 s, he would give the merry-go-round an angular velocity of 13.3 rad/s when it is empty but only 8.89 rad/s when the child
is on it. In terms of revolutions per second, these angular velocities are 2.12 rev/s and 1.41 rev/s, respectively. The father would end up running
at about 50 km/h in the first case. Summer Olympics, here he comes! Confirmation of these numbers is left as an exercise for the reader.
Check Your Understanding
Torque is the analog of force and moment of inertia is the analog of mass. Force and mass are physical quantities that depend on only one
factor. For example, mass is related solely to the numbers of atoms of various types in an object. Are torque and moment of inertia similarly
simple?
Solution
No. Torque depends on three factors: force magnitude, force direction, and point of application. Moment of inertia depends on both mass and its
distribution relative to the axis of rotation. So, while the analogies are precise, these rotational quantities depend on more factors.
10.4 Rotational Kinetic Energy: Work and Energy Revisited
In this module, we will learn about work and energy associated with rotational motion. Figure 10.14 shows a worker using an electric grindstone
propelled by a motor. Sparks are flying, and noise and vibration are created as layers of steel are pared from the pole. The stone continues to turn
even after the motor is turned off, but it is eventually brought to a stop by friction. Clearly, the motor had to work to get the stone spinning. This work
went into heat, light, sound, vibration, and considerable rotational kinetic energy.


330 CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM
Figure 10.14 The motor works in spinning the grindstone, giving it rotational kinetic energy. That energy is then converted to heat, light, sound, and vibration. (credit: U.S. Navy photo by Mass Communication Specialist Seaman Zachary David Bell)
Work must be done to rotate objects such as grindstones or merry-go-rounds. Work was defined in Uniform Circular Motion and Gravitation for
translational motion, and we can build on that knowledge when considering work done in rotational motion. The simplest rotational situation is one in
which the net force is exerted perpendicular to the radius of a disk (as shown in Figure 10.15) and remains perpendicular as the disk starts to rotate.
The force is parallel to the displacement, and so the net work done is the product of the force times the arc length traveled:
(10.53)
net W = (net F)Δ s.
To get torque and other rotational quantities into the equation, we multiply and divide the right-hand side of the equation by r , and gather terms:
(10.54)
net W = ( r net F)Δ s
r .
We recognize that r net F = net τ and Δ s / r = θ , so that
(10.55)
net W = (net τ) θ.
This equation is the expression for rotational work. It is very similar to the familiar definition of translational work as force multiplied by distance. Here,
torque is analogous to force, and angle is analogous to distance. The equation net W = (net τ) θ is valid in general, even though it was derived for
a special case.
To get an expression for rotational kinetic energy, we must again perform some algebraic manipulations. The first step is to note that net τ = Iα , so
that
(10.56)
net W = Iαθ.
Figure 10.15 The net force on this disk is kept perpendicular to its radius as the force causes the disk to rotate. The net work done is thus (net F)Δ s . The net work goes into rotational kinetic energy.
Making Connections
Work and energy in rotational motion are completely analogous to work and energy in translational motion, first presented in Uniform Circular
Motion and Gravitation.
Now, we solve one of the rotational kinematics equations for αθ . We start with the equation
2
(10.57)
ω 2 = ω 0 + 2 αθ.
Next, we solve for αθ :
2
(10.58)
αθ = ω 2 − ω 0
2
.
Substituting this into the equation for net W and gathering terms yields
CHAPTER 10 | ROTATIONAL MOTION AND ANGULAR MOMENTUM 331
2
(10.59)
net W = 12 Iω 2 − 12 Iω 0 .
This equation is the work-energy theorem for rotational motion only. As you may recall, net work changes the kinetic energy of a system. Through
<











