CH 3: That's my Birthday!
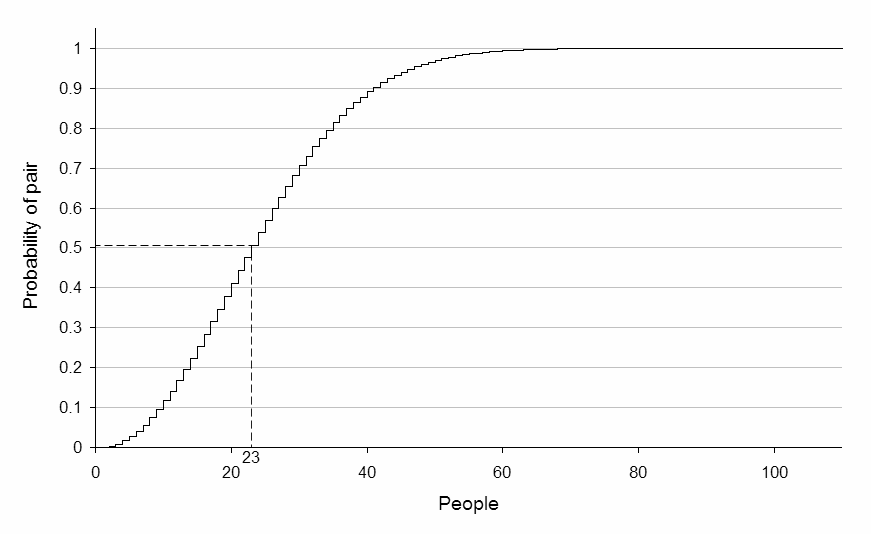
So, this chapter is about a well-known phenomenon called the “Birthday Paradox” but in reality it is not so much a paradox as it is an unexpected resulting probability of a given event. Let me explain. The idea here is that you are given 23 totally random people. (Segue into randomness in chapter 26.) You are reminded that of course there are 365 different days on which you can call your birthday; the leap year would count as .25 of a day, occurring once every four years. You are then asked what percentage chance, say 0-100%, that any two of these 23 people maintain the same birthday.
The truth is that there is a slightly better than 50% chance of there being two people with the same birthday. This means the chances are a bit better then guessing on the flip of a coin. Additionally, if you were to have a relatively paltry 57 people to test the experiment, you have the surprising guarantee of more than 99% certainty of matching two birthdays.
This fact is true because every person's birthday is being compared with everyone else's birthday. This means that if you were to create unique pairs of people from the 23 people, you can obtain 253 different pairs of people. By considering the group of 23 people in terms of the numbers of unique pairs, 253, rather than the number of individuals, 23, the result becomes less surprising. The mathematics involved does assume a perfect distribution of birthdays, meaning any given birthday has an equal probability of happening with any other given birthday, and in reality certain birthdays are in fact more common than others. This skew of the distribution of birthdays does not really affect results much when actually attempting the experiment. The math involved in the birthday paradox is a cousin of the pigeonhole principle. In the pigeonhole principle, if you have n pigeons and p holes and 1 < p < n, then you are assured that at least one of the holes will contain two pigeons. This is the same logic that ensures that if you know someone has three children, you know that at least two of the children are of the same gender.