CHAPTER 4
CONCRETE STRENGTH
L. Dvorkin and O.Dvorkin





Strength is a property of materials to resist to destruction under action of
the external loading.
4.1. Theories of strength and mechanism
of destruction
The existing theories of concrete strength are divided into three
groups: phenomenological, statistical and structural.
Phenomenological theories consider concrete, as homogeneous
isotropic material. All attention is paid to dependence of strength on
the external loading, they set reasons on which it is possible to judge
about beginning of material destruction at the tense state, if the
behavior at simple tension, compression or shear is known.
71





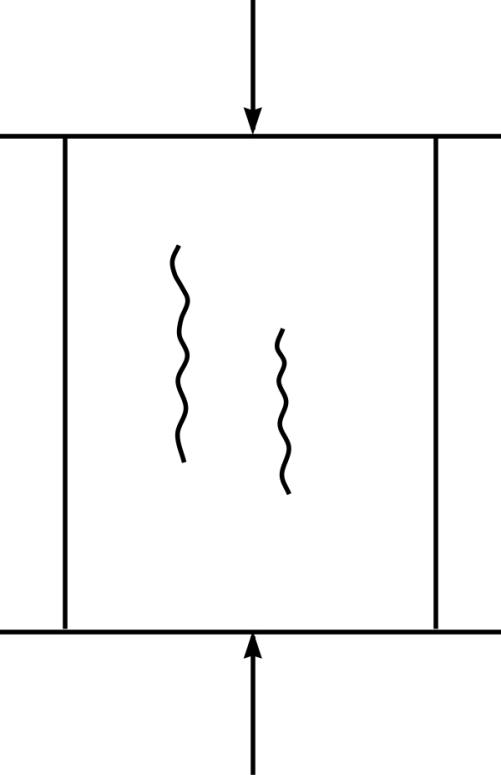
According to statistical theories
the existence in the concrete of
continuous isotropic environment,
in which there are microscopic
cracks (conformable to the
statistical laws) is also assumed.
These theories allow to explain
enormous distinction between
theoretical and actual strength,
determined by the defects of
structure of substance, without
consideration of structure.
Fig. 4.1. Chart of destruction of
easily broken material at the
axial compression if there is
default of friction on supporting
flags of the press
72





Development of crack under action of the attached compression takes place
at reduction of general energy of the system. Stability Criterion of easily
broken material with a crack: can be calculated by the following formula:
σ = 2Еν / l
π
,
(4
.1)
where σ-the attached compression; E-modulus of elasticity;
ν-surface energy; l- length of crack.
In accordance with the statistical theory of the strength (from Weibull)
tensile and flexural strength (R) changes inversely proportional to a
volume υ:
А
R =
(4



















