,
τ
el
pl
shr
where ε - elastic deformation; ε - plastic deformation;
el
pl
ε - deformation of shrinkage.
shr
88






On the idealized chart of
compression of cement stone it
is possible to select three basic
areas: a-b-absence of cracks in
the structure of cement stone; bc-appearance of microscopic
cracks;
с-ddestruction of
cement stone as a result of
spontaneous formation of
growing cracks.
For description of cement stone
and concrete deformation under
loading a number of rheological
models are offered.
Fig. 5.1. The idealized chart of
deformations in cement stone at the
axial compression (at rapid loading)
ε - deformation; σ - stress
89





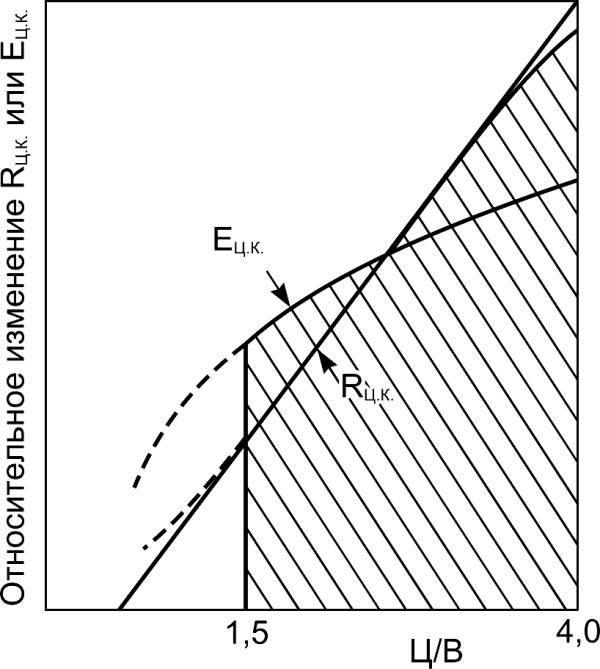
There is a large number of
formulas describing elastic
s
properties of concrete. Their
c.
kind depends on the accepted
or E
Ec.s
model of stresses distributing,
sc.
character of location of
f R
aggregates particles and other
oge
reasons.
n
R
a
c.s
Ch
1.5
C/W
4.0
Fig. 5.2. Typical relationship between
modulus of elasticity Ec.s , strength of
cement stone Rc.s and cement-water
ratio (C/W)
90





Modulus of concrete elasticity (E) depends on concrete strength. For
calculation of the modulus of elasticity at loading of concrete at age of
hardening (τ) following equations are using:
E R
E
m
τ
=




















