,
(6
.3)
k
W − 5
.
0 αC +
1
(
1000 − К )
f
.
c
where К – compacting factor of concrete; C, W-quantities of cement
c.f
and mixing water, kg/m3; α - degree of cement hydration.
For calculation of a degree of cement hydration (α) its relationship with
compressive strength of the cement stone can be used. For example,
T.Pawers presented this dependence in the form of the formula:
R
= 238α3,
(6.4)
c.s
where R
- compressive strength of the cement stone (MPa).
c.s
112





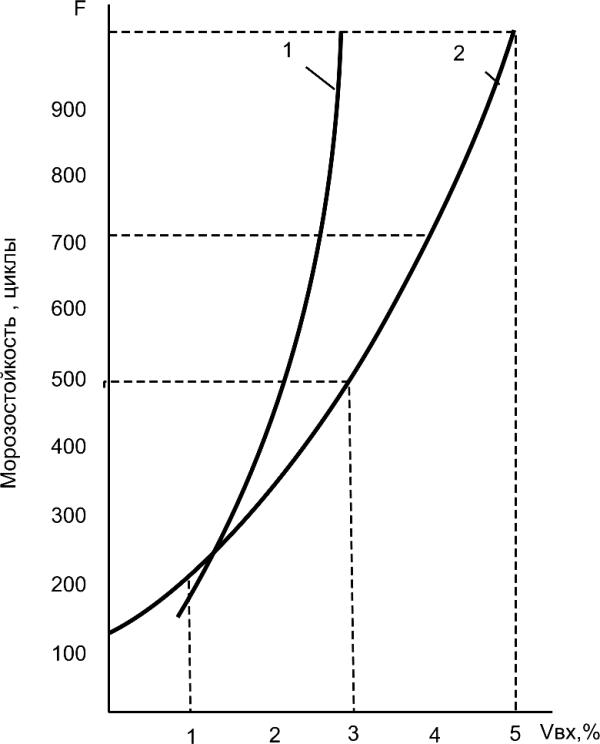
Comparison of calculated values of
frost resistance under the formula (6.1)
and experimental values of Portland
Cement Association are shown in
and thawing
ng
Fig.6.3.
zie
s of fre
The American data differ higher
e, cycle
values of frost resistance at V ≥2%,
air
that it is possible to explain higher
normalized decrease of strength of
ost resistanc
concrete specimens - 25 % instead of
Fr
5 %.
Air
content, %
Fig.6.3. Effect of entrained air on frost
resistance of concrete:
1 – from laboratory tests (PCA data); 2 – from
formula (6.1) (α = 0,7, К= 170, C = 400 kg/m3,
W = 200 kg/m3)
113





6.2. Concrete resistance to temperature influences
Temperature rise at hardening of concrete accelerates chemical reactions of
hydration and positively influences on growth of concrete strength. Essential
acceleration of hardening processes begins at temperatures from 70 to 95°C
and especially at 170 to 200°C. However at not enough quantity of mixing
water in concrete mixture influence of the raised temperatures slows down
process of hydration and reduces strength of concrete.
For production of durable concrete it is important to reduce to minimum its
deformation at temperature influence.
Occurrence of thermal strains in concrete probably not only at its external
heating, but also as a result of a self-heating due to exothermic reaction of
hydration.
114





Formation of cracks in massive concrete
structures usually has thermal character.
Criterion К characterizes thermal cracks
t
resistance:
J k
ε
⋅ С ⋅ ρ
К
s
.
m
=




















