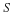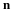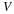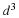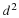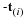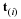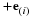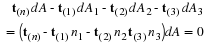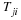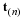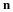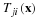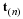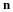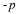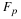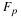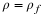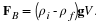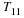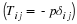Fluid motion will be described as the motion of a "particle" that occupies a point in space. At some time, say t=0, a fluid particle is at a position and at a later time the same particle is at a position x. The motion of the particle that occupied this original position is described as follows.

(4.1)

The initial coordinates ξ of a particle will be referred to as the material coordinates of the particles and, when convenient, the particle itself may be called the particle ξ . The terms convected and Lagrangian coordinates are also used. The spatial coordinates x of the particle may be referred to as its position or place. It will be assumed that the motion is continuous, single valued and the previous equation can be inverted to give the initial position or material coordinates of the particle which is at any position x at time t; i.e.,

(4.2)

are also continuous and single valued. Physically this means that a continuous arc of particles does not break up during the motion or that the particles in the neighborhood of a given particle continue in its neighborhood during the motion. The single valuedness of the equations mean that a particle cannot split up and occupy two places nor can two distinct particles occupy the same place. Exceptions to these requirements may be allowed on a finite number of singular surfaces, lines or points, as for example a fluid divides around an obstacle. It is shown in Appendix B that a necessary and sufficient condition for the inverse functions to exist is that the Jacobian

()

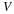
should not vanish.

The transformation x=x(ξ,t) may be looked at as the parametric equation of a curve in space with t as the parameter. The curve goes through the point ξ , corresponding to the parameter t=0, and these curves are the particle paths. Any property of the fluid may be followed along the particle path. For example, we may be given the density in the neighborhood of a particle as a function ρ(ξ,t), meaning that for any prescribed particle ξ we have the density as a function of time, that is, the density that an observer riding on the particle would see. (Position itself is a "property" in this general sense so that the equations of the particle path are of this form.) This material description of the change of some property, say ℑ(ξ,t), can be changed to a spatial description ℑ(x,t).

Physically this says that the value of the property at position x at time t is the value appropriate to the particle that is at x at time t. Conversely, the material description can be derived from the spatial one.

meaning that the value as seen by the particle at time t is the value at the position it occupies at that time.

(4.5)

and

(4.6)

Thus ∂ℑ/∂t is the rate of change of ℑ as observed at a fixed point x, whereas Dℑ/Dt is the rate of changed as observed when moving with the particle, i.e., for a fixed value of ξ . The latter we call the material derivative. It is also called the convected, convective, or substantial derivative and often denoted by D/Dt. In particular the material derivative of the position of a particle is it velocity. Thus putting ℑ=x_i, we have

(4.7)

or

(4.8)

This allows us to establish a connection between the two derivatives, for

(4.9)

We now have a formal definition of the velocity field as a material derivative of the position of a particle.

(4.10)

The field line lines of the velocity field are called streamlines; they are the solutions of the three simultaneous equations

(4.11)

where s is a parameter along the streamline. This parameter s is not to be confused with the time, for in the above equation t is held fixed while the equations are integrated, and the resulting curves are the streamlines at the instantt. These may vary from instant to instant and in general will not coincide with the particle paths.

To obtain the particle paths from the velocity field we have to follow the motion of each particle. This means that we have to solve the differential equations

(4.12)

subject to x=ξ at t=0. Time is the parameter along the particle path. Thus the particle path is the trajectory taken by a particle.

The flow is called steady if the velocity components are independent of time. For steady flows, the parameter s along the streamlines may be taken to be t and the streamlines and particle paths will coincide. The converse does not follow as there are unsteady flows for which the streamlines and particle paths coincide.

If C is a closed curve in the region of flow, the streamlines through every point of C generate a surface known as a stream tube. Let S be a surface with C as the bounding curve, then

(4.13)

is known as the strength of the stream tube at its cross-section S.

The acceleration or the rate of change of velocity is defined as

(4.14)

Notice that in steady flow this does not vanish but reduces to

(4.15)

Even in steady flow other than a constant translation, a fluid particle will accelerate if it changes direction to go around an obstacle or if it increases its speed to pass through a constriction.

The name streakline is applied to the curve traced out by a plume of smoke or dye, which is continuously injected at a fixed point but does not diffuse. Thus at time t the streakline through a fixed-point y is a curve going from y to x(y,t), the position reached by the particle which was at y at time t=0. A particle is on the streakline if it passed the fixed-point y at some time between 0 and t. If this time was t^', then the material coordinates of the particle would be given by 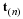. However, at time t this particle is at x=x(ξ,t) so that the equation of the streakline at time t is given by

(4.16)

where the parameter t^' along it lies in the interval 0≤t^'≤t. If we regard the motion as having been proceeding for all time, then the origin of time is arbitrary and t' can take negative values –∞≤t^'≤t.

The flow field illustrated in 4.13 by Aris is assigned as an exercise.

We noticed earlier that if the coordinate system is changed from coordinates ξ to coordinates x, then the element of volume changes by the formula

(4.17)

If we think of ξ as the material coordinates, they are the Cartesian coordinates at t=0, so that dξ₁dξ₂dξ₃ is the volume dV_o of an elementary rectangular parallelepiped. Consider this elementary parallelepiped about a given point ξ at the initial instant. By the motion this parallelepiped is moved and distorted but because the motion is continuous it cannot break up and so at some time t is some neighborhood of the point x=x(ξ,t). By the above equation, its volume is 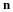and hence

(4.18)

It is called the dilation or expansion. The assumption that x=x(ξ,t) can be inverted to give ξ=ξ(x,t), and vice versa, is equivalent to requiring that neither J nor J^–1 vanish. Thus,

We can now ask how the dilation changes as we follow the motion. To answer this we calculate the material derivative DJ/Dt. However,

(4.20)

Now

(4.21)

for D/Dt is differentiation with ξ constant so that the order can be interchanged. Now if we regard v_i as a function of x₁, x₂, x₃,

(4.22)

The above relation can now be applied to differentiation of the Jacobian.

(4.23)

where we made use of the property of the determinant that the determinant of a matrix with repeated rows is zero. Thus,

(4.24)

We thus have an important physical meaning for the divergence of the velocity field. It is the relative rate of dilation following a particle path. It is evident that for an incompressible fluid motion,

(4.25)

In the cases of flow of an incompressible fluid, and of steady flow of a compressible fluid, the mass-conservation equation reduces to the statement that a vector divergence is zero, the divergences being of u and ρu respectively. If we impose the further restriction that the flow field either is two-dimensional or has axial symmetry, this vector divergence is the sum of only two derivatives, and the mass-conservation equation can then be regarded as defining a scalar function from which the components of u or ρu are obtained by differentiation. The procedure will be described here for the case of an incompressible fluid.

Assume first that the motion is two-dimensional, so that u=(u,v,0) and u and v are independent of z. The mass-conservation equation for an incompressible fluid then has the form

(4.26)

from which it follows that uδy–vδx is an exact differential, equal to δψ say. Then

(4.27)

and the unknown scalar function ψ(x,y,t) is defined by

(4.28)

where ψ_o is a constant and the line integral is taken along an arbitrary curve joining some reference point O to the point P with co-ordinates x, y. In this way we have used the mass-conservation equation to replace the two dependent variables u, v by the single dependent variable ψ , which is a very valuable simplification in many ca