HOCN
5.5×10-3
5.5%
H Cl O 2
2.8×10-2
28.2%
CH 3 COOH (acetic acid)
1.3×10-3
1.3%
CH 3 CH 2 COOH (propionic acid) 1.1×10-3
1.1%
We might be tempted to conclude from Table 5.2 that we can characterize the strength of each acid by the percent ionization of acid molecules in solution. However, before doing so, we observe
the pH of a single acid, nitrous acid, in solution as a function of the concentration of the acid.
(5.2)
In this case, "concentration of the acid" refers to the number of moles of acid that we dissolved
per liter of water. Our observations are listed in Table 5.3, which gives
, pH, and percent
ionization as a function of nitrous acid concentration.
Table 5.3. % Ionization of Nitrous
Acid
c0 (M)
pH % Ionization
0.50
1.7×10-2 1.8 3.3%
0.20
1.0×10-2 2.0 5.1%
0.10
7.0×10-3 2.2 7.0%
0.050
4.8×10-3 2.3 9.7%
0.020
2.9×10-3 2.5 14.7%
0.010
2.0×10-3 2.7 20.0%
0.005
1.3×10-3 2.9 26.7%
0.001
4.9×10-4 3.3 49.1%
0.0005 3.0×10-4 3.5 60.8%
Surprisingly, perhaps, the percent ionization varies considerably as a function of the concentration









of the nitrous acid. We recall that this means that the fraction of molecules which ionize,
according to Equation 5.2, depends on how many acid molecules there are per liter of solution.
Since some but not all of the acid molecules are ionized, this means that nitrous acid molecules
are present in solution at the same time as the negative nitrite ions and the positive hydrogen ions.
Recalling our observation of equilibrium in gas phase reactions, we can conclude that
Equation 5.2 achieves equilibrium for each concentration of the nitrous acid.
Since we know that gas phase reactions come to equilibrium under conditions determined by the
equilibrium constant, we might speculate that the same is true of reactions in aqueous solution,
including acid ionization. We therefore define an analogy to the gas phase reaction equilibrium
constant. In this case, we would not be interested in the pressures of the components, since the
reactants and products are all in solution. Instead, we try a function composed of the equilibrium
concentrations:
(5.3)
The concentrations at equilibrium can be calculated from the data in Table 5.3 for nitrous acid.
is listed and
. Furthermore, if c 0 is the initial concentration of the acid defined
by the number of moles of acid dissolved in solution per liter of solution, then
.
Note that the contribution of
to the value of the function K is simply a constant. This is
because the "concentration" of water in the solution is simply the molar density of water,
, which is not affected by the presence or absence of solute. All of the relevant
concentrations, along with the function in Equation 5.3 are calculated and tabulated in Table 5.4.
Table 5.4. Equilibrium Concentrations and K for
Nitrous Acid
c0 (M)
K
0.50
1.7×10-2 1.7×10-2 0.48
1.0×10-5
0.20
1.0×10-2 1.0×10-2 0.19
9.9×10-6
0.10
7.0×10-3 7.0×10-3 9.3×10-2 9.6×10-6
0.050
4.8×10-3 4.8×10-3 4.5×10-2 9.4×10-6
0.020
2.9×10-3 2.9×10-3 4.5×10-2 9.4×10-6
0.010
2.0×10-3 2.0×10-3 8.0×10-3 8.9×10-6
0.005
1.3×10-3 1.3×10-3 3.6×10-3 8.8×10-6
0.001
4.9×10-4 4.9×10-4 5.1×10-4 8.5×10-6

0.0005 3.0×10-4 3.0×10-4 2.0×10-4 8.5×10-6
We note that the function K in Equation 5.3 is approximately, though only approximately, the same for all conditions analyzed in Table 5.3. Variation of the concentration by a factor of 1000
produces a change in K of only 10% to 15%. Hence, we can regard the function K as a constant
which approximately describes the acid ionization equilibrium for nitrous acid. By convention,
chemists omit the constant concentration of water from the equilibrium expression, resulting in
the acid ionization equilibrium constant, Ka, defined as:
(5.4)
From an average of the data in Table 5.4, we can calculate that, at 25°C for nitrous acid, Ka=5×10-4. Acid ionization constants for the other weak acids in Table 5.2 are listed in Table 5.5.
Table 5.5. Weak Acid Ionization Constants, Ka
and pKa
Acid
Ka
p Ka
HNO 2
5×10-4
3.3
HCN
4.9×10-10 9.3
HIO
2.3×10-11 10.6
HF
3.5×10-4 3.4
HOCN
3.5×10-4 3.4
H Cl O 2
1.1×10-2 2.0
CH 3 COOH (acetic acid)
1.7×10-5 4.8
CH 3 CH 2 COOH (propionic acid) 1.4×10-5 4.9
We make two final notes about the results in Table 5.5. First, it is clear the larger the value of Ka, the stronger the acid. That is, when Ka is a larger number, the percent ionization of the acid is
larger, and vice versa. Second, the values of Ka very over many orders of magnitude. As such, it is
often convenient to define the quanity pKa, analogous to pH, for purposes of comparing acid
strengths:










(5.5)
pKa=–(log Ka)
The value of pKa for each acid is also listed in Table 5.5. Note that a small value of pKa implies a large value of Ka and thus a stronger acid. Weaker acids have larger values of pKa. Ka and pKa thus give a simple quantitative comparison of the strength of weak acids.
Observation 3: Autoionization of Water
Since we have the ability to measure pH for acid solutions, we can measure pH for pure water as
well. It might seem that this would make no sense, as we would expect
to equal zero exactly
in pure water. Surprisingly, this is incorrect: a measurement on pure water at 25°C yields pH=7,
so that
. There can be only one possible source for these ions: water molecules.
The process
(5.6)
is referred to as the autoionization of water. Note that, in this reaction, some water molecules
behave as acid, donating protons, while other water molecules behave as base, accepting protons.
Since at equilibrium
, it must also be true that
. We can write the
equilibrium constant for Equation 5.6, following our previous convention of omitting the pure water from the expression, and we find that, at 25°C,
(5.7)
(In this case, the subscript "w" refers to "water".)
Equation 5.6 occurs in pure water but must also occur when ions are dissolved in aqueous solutions. This includes the presence of acids ionized in solution. For example, we consider a
solution of 0.1M acetic acid. Measurements show that, in this solution
and
. We note two things from this observation: first, the value of
is considerably
less than in pure water; second, the autoionization equilibrium constant remains the same at
1.0×10-14. From these notes, we can conclude that the autoionization equilibrium of water occurs
in acid solution, but the extent of autoionization is suppressed by the presence of the acid in
solution.
We consider a final note on the autoionization of water. The pH of pure water is 7 at 25°C. Adding
any acid to pure water, no matter how weak the acid, must increase
, thus producing a pH
below 7. As such, we can conclude that, for all acid solutions, pH is less than 7, or on the other
hand, any solution with pH less than 7 is acidic.



Observation 4: Base Ionization, Neutralization and Hydrolysis of
Salts
We have not yet examined the behavior of base molecules in solution, nor have we compared the
relative strengths of bases. We have defined a base molecule as one which accepts a positive
hydrogen ion from another molecule. One of the most common examples is ammonia, NH 3. When
ammonia is dissolved in aqueous solution, the following reaction occurs:
(5.8)
Due to the lone pair of electrons on the highly electronegative N atom, NH 3 molecules will readily
attach a free hydrogen ion forming the ammonium ion NH +
4 . When we measure the concentration
of OH– for various initial concentration of NH 3 in water, we observe the results in Table 5.6. We should anticipate that a base ionization equilibrium constant might exist comparable to the acid
ionization equilibrium constant, and in Table 5.6, we have also calculated the value of the function Kb defined as:
(5.9)
Table 5.6. Equilibrium
Concentrations and Kb for
Ammonia
c0 (M)
Kb
pH
0.50
3.2×10-3 2.0×10-5 11.5
0.20
2.0×10-3 2.0×10-5 11.3
0.10
1.4×10-3 2.0×10-5 11.1
0.050
9.7×10-4 1.9×10-5 11.0
0.020
6.0×10-4 1.9×10-5 10.8
0.010
4.2×10-4 1.9×10-5 10.6
0.005
3.0×10-4 1.9×10-5 10.5
0.001
1.3×10-4 1.8×10-5 10.1
0.0005 8.7×10-5 1.8×10-5 9.9



Given that we have dissolved a base in pure water, we might be surprised to discover the presence
of positive hydrogen ions, H 3 O+, in solution, but a measurement of the pH for each of the
solutions reveals small amounts. The pH for each solution is also listed in Table 5.6. The source of these H 3 O+ ions must be the autoionization of water. Note, however, that in each case in basic solution, the concentration of H 3 O+ ions is less than that in pure water. Hence, the presence of the base in solution has suppressed the autoionization. Because of this, in each case the pH of a basic
solution is greater than 7.
Base ionization is therefore quite analogous to acid ionization observed earlier. We now consider
a comparison of the strength of an acid to the strength of a base. To do so, we consider a class of
reactions called "neutralization reactions" which occur when we mix an acid solution with a base
solution. Since the acid donates protons and the base accepts protons, we might expect, when
mixing acid and base, to achieve a solution which is no longer acidic or basic. For example, if we
mix together equal volumes of 0.1M H Cl(aq) and 0.1M Na OH(aq), the following reaction occurs:
(5.10)
The resultant solution is simply a salt solution with NaCl dissolved in water. This solution has neither acidic nor basic properties, and the pH is 7; hence the acid and base have neutralized each
other. In this case, we have mixed together a strong acid with a strong base. Since both are strong
and since we mixed equal molar quantities of each, the neutralization reaction is essentially
complete.
We next consider mixing together a weak acid solution with a strong base solution, again with
equal molar quantities of acid and base. As an example, we mix 100ml of 0.1M acetic acid ( HA)
solution with 100ml of 0.1M sodium hydroxide. In this discussion, we will abbreviate the acetic
acid molecular formula CH 3 COOH as HA and the acetate ion CH 3 COO– as A–. The reaction of HA
and NaOH is:
(5.11)
is the acetate ion in solution, formed when an acetic acid molecule donates the positive
hydrogen ion. We have thus created a salt solution again, in this case of sodium acetate in water.
Note that the volume of the combined solution is 200ml, so the concentration of sodium acetate
( NaA) in solution is 0.050M.
Unlike our previous NaCl salt solution, a measurement in this case reveals that the pH of the
product salt solution is 9.4, so the solution is basic. Thus, mixing equal molar quantities of strong
base with weak acid produces a basic solution. In essence, the weak acid does not fully neutralize
the strong base. To understand this, we examine the behavior of sodium acetate in solution. Since
the pH is greater than 7, then there is an excess of OH– ions in solution relative to pure water.
These ions must have come from the reaction of sodium acetate with the water. Therefore, the
negative acetate ions in solution must behave as a base, accepting positive hydrogen ions:




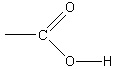
(5.12)
The reaction of an ion with water to form either an acid or a base solution is referred to as
hydrolysis. From this example, the salt of a weak acid behaves as a base in water, resulting in a
pH greater than 7.
To understand the extent to which the hydrolysis of the negative ion occurs, we need to know the
equilibrium constant for this reaction. This turns out to be determined by the acid ionization
constant for HA. To see this, we write the equilibrium constant for the hydrolysis of A– as (5.13)
Multiplying numerator and denominator by
, we find that
(5.14)
Therefore, for the hydrolysis of acetate ions in solution, Kh=5.8×10-10. This is fairly small, so the
acetate ion is a very weak base.
Observation 5: Acid strength and molecular properties
We now have a fairly complete quantitative description of acid-base equilibrium. To complete our
understanding of acid-base equilibrium, we need a predictive model which relates acid strength or
base strength to molecular properties. In general, we expect that the strength of an acid is related
either to the relative ease by which it can donate a hydrogen ion or by the relative stability of the
remaining negative ion formed after the departure of the hydrogen ion.
To begin, we note that there are three basic categories of acids which we have examined in this
study. First, there are simple binary acids: HF; HCl; HBr; HI. Second, there are acids formed from main group elements combined with one or more oxygen atoms, such H 2 SO 4 or HNO 3. These are called oxyacids. Third, there are the carboxylic acids, organic molecules which contain the
carboxylic functional group in Figure 5.1.
Figure 5.1. Carboxylic Functional Group
We consider first the simple binary acids. HCl, HBr, and HI are all strong acids, whereas HF is a weak acid. In comparing the experimental values of pKa values in Table 5.7, we note that the acid

strength increases in the order HF< HCl< HBr< HI. This means that the hydrogen ion can more readily separate from the covalent bond with the halogen atom (X) as we move down the periodic
table. This is reasonable, because the strength of the H-X bond also decreases as we move down
the periodic table, as shown in Table 5.7.
Table 5.7. H-X Bond Strengths
and pKa
pKa Bond Energy (
)
HF
3.1 567.7
HCl -6.0 431.6
HBr -9.0 365.9
HI
-9.5 298.0
The decreasing strength of the H-X bond is primarily due to the increase is the size of the X atom
as we move down the periodic table. We conclude that one factor which influences acidity is the
strength of the H-X bond: a weaker bond produces a stronger acid, and vice versa.
In the acids in the other two categories, the hydrogen atom which ionizes is attached directly to an
oxygen atom. Thus, to understand acidity in these molecules, we must examine what the oxygen
atom is in turn bonded to. It is very interesting to note that, in examining compounds like R-O-H,
where R is an atom or group of atoms, we can get either acidic or basic properties. For examples,
NaOH is a strong base, whereas HOCl is a weak acid. This means that, when NaOH ionizes in solution, the Na-O linkage ionizes, whereas when HOCl ionizes in solution, the H-O bond ionizes.
To understand this behavior, we compare the strength of the simple oxyacids HOI, HOBr, and
HOCl. The pKa's for these acids are found experimentally to be, respectively, 10.6, 8.6, and 7.5.
The acid strength for HOX increases as we move up the periodic table in the halogen group. This
means that the H-O bond ionizes more readily when the oxygen atom is bonded to a more
electronegative atom.
We can add to this observation by comparing the strengths of the acids HOCl, HOClO, HO Cl O 2, and HO Cl O 3. (Note that the molecular formulae are more commonly written as HClO, H Cl O 2, H Cl O 3, and H Cl O 4. We have written them instead to emphasize the molecular structure.) The pKa's of these acids are, respectively, 7.5, 2.0, -2.7, and -8.0. In each case, the molecule with more
oxygen atoms on the central Cl atom is the stronger acid: HOClO is more acidic than HOCl, etc.
A similar result is found in comparing the oxyacids of nitrogen. HONO 2, nitric acid, is one of the
strong acids, whereas HONO, nitrous acid, is a weak acid. Since oxygen atoms are very strongly
electronegative, these trends add to our observation that increasing electronegativity of the
attached atoms increases the ionization of the O-H bond.
Why would electronegativity play a role in acid strength? There are two conclusions we might
draw. First, a greater electronegativity of the atom or atoms attached to the H-O in the oxyacid
apparently results in a weaker H-O bond, which is thus more readily ionized. We know that an
electronegative atom polarizes bonds by drawing the electrons in the molecule towards it. In this
case, the Cl in HOCl and the Br in HOBr must polarize the H-O bond, weakening it and facilitating the ionization of the hydrogen. In comparing HOCl to HOClO, the added oxygen atom must increase the polarization of the H-O bond, thus weakening the bond further and increasing



































