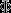Part One
5
Consider a glass biconcave lens with refractive index n = . Each face has a
3
radius of curvature equal to 12 cm and their vertices are 1.2 cm apart, following
a sketch drawn using an appropriate scale going from left to right.
1-1 Give the correct algebraic values for the variables used in the equations.
a.) S C = R = +12 cm
1
1
1
b.) S C = R = +12 cm;
2
2
2
c.) e = S S = +12 mm;
1 2
d.) S C = R = -12 cm;
1
1
1
e.) S C = R = -12cm;
2
2
2
f.) e = S S = -12 mm.
1 2
Check off the right answer(s).
1-2 Calculate the lens’ image focal length.
The image focal length Φ is:
a.) 90 mm;
b.) 88.235 mm
c.) -90 mm ;
d.) -88.235 mm
Check off the right answer(s).

African Virtual University
1-3 If we consider that the distance between the vertices is negligible for the radii
of curvature, which answer describes the correct focal length value?
a.) 90 mm ;
b.) 88.235 mm
c.) -90 mm ;
d.) -88.235 mm
Check off the right answer(s).
1-4 What is the approximation error?
The approximation error is :
a.) 20%
b.) 5%
c.) 2%
d.) 0.5%
Check off the right answer(s).
2- Recall the expression for the optical center.
3- Calculate the position of a lens’ optical center.
4- Geometrically interpret the optical center’s position for different types of
lenses.
5- Part Two
5-1 Once again using the biconcave lens, calculate the position of the lens’ optical
center.
The position of the lens’ optical center OS is:
2
a.) 0
b.) + 2mm
c.) + 6mm
d.) - 2mm
e.) - 6 mm
Check off the right answer(s).

African Virtual University
5-2 Geometrically interpret the value of the position of the optical center.
The optical center is:
a.) merged into the lens’ left vertex;
b.) between the middle of the lens and its left vertex;
c.) in the middle of the lens;
d.) between the middle of the lens and its right vertex;
e.) merged into the lens’ right vertex;
Check off the right answer(s)
6- Under which conditions can a lens’ thickness be considered negligible with
the optical center merged into the middle of the lens?
7- Define a thin lens.
8- A biconvex lens approximated to a thin lens is:
a.) convergent;
b.) divergent;
c.) of focal length 90 mm;
e.) of focal length 88.235 mm
f.) of focal length -90 mm;
g.) of focal length -88.235 mm
Check off the right answer(s)
9- Determine the focal lengths for a thin lens.
10- Give a geometrical interpretation of the characteristics for a thin lens.
11- Graphically determine the image of an object.
12- Graphically determine the emerging ray for an incident ray.
13 : Calculate the image and object focal lengths for a biconvex thin lens.
13-1 : The image focal length is :
a. +180 mm
b. +300 mm
c. + 88.235 mm
d. -180 mm
e. -300 mm
f. - 88.235 mm
Check off the right answer(s).

African Virtual University
13-2 : The object focal length is:
a. +180 mm
b. +300 mm
c. + 88.235 mm
d. -180 mm
e. -300 mm
f. - 88.235 mm
Check off the right answer(s).
14- Using the conjugate formulas for centered systems, write the conjugate
equations for thin lenses.
15- Part Three:
Determine the position of the thin lens’ principal planes.
15-1. The position of the image’s principal plane defined as S
is equal to:
2H ʹ
a.) +3.53 mm
b.) +3.235 mm
c.) -3.53 mm
d.) -3.235 mm
Check off the right answer(s)
15-2 The position of the object’s principal plane defined as S H is equal to:
1
a.) +3.53 mm
b.) +3.235 mm
c.) -3.53 mm
d.) -3.235 mm
Check off the right answer(s)
Learning Activity
The learners must complete all of the recommended reading before answering
the questions. They must complete all of the exercises. They will be divided
into work groups. Each group must solve the problems and will designate a spo-
kesperson. After a certain amount of time (4 hours) decided by the tutor, each
spokesperson will write up a report, making sure that the first and last name of
each group member is included, and will then send their report by e-mail to the
tenured teacher for the course.

African Virtual University 0
Answer Key
Question 1-1 : b. ; c. ; d. ; Comments: The distances are algebraic values and are
defined from left to right.
Give the correct algebraic values for the variables used in the equations
a. You have mixed up the variables.
b. Great answer, the distances are indeed algebraic values defined from left
to right.
c. Great answer, the distances are indeed algebraic values defined from left
to right..
d. Great answer, the distances are indeed algebraic values defined from left
to right.
e. Careful, you have not correctly identified the variables.
f. Try again.
Question 1-2 :
a. Careful, this is a diverging lens.
b. You are confused between a diverging and a converging lens.
c. Think it through before answering.
d. Good answer, the lens is divergent and we did not use the thin lens ap-
proximation.
Question 1-3
a. Reread the question before answering.
b. Think it through some more.
c. Great answer, the lens is indeed divergent and we consider its thickness
to be negligible.
Question 1-4
a. Try again.
b. Reread the question before trying again.
c. Very good.

African Virtual University
Question 2.
A lens’ optical center O is a point on the axis belonging to the refractive medium
n, that can be inside or outside the segment S S , in a way that every ray that
1 2
travels through the lens and intersecting that point has a parallel emerging ray
and incident ray.
Good answer, You have understood the question.
Question 3: Point O divides the segment S S in the relation between the radii of
1 2
curvature’s algebraic values and is therefore unique. O does not depend on the
refractive index for the glass that the thick lens is made of. O is positioned between
S and S if R and R are of opposite signs. O is outside of S S if R and R are
1
2
1
2
1 2
1
2
of the same sign. O is always closest to the face with the most curvature.

African Virtual University
OS
R
R
Therefore:
1
1
1
=
⇒ OS = e
1
OS −OS
R − R
R − R
2
1
2
1
2
1
OS −OS
R − R
R
In the same way:
2
1
2
1
2
=
⇒ OS = e
2
OS
R
R − R
2
2
2
1
Perfect answer.
Question 4: The optical center O is the image of the lens’ object nodal point N
through the entrance boundary, where the image of the optical center O through
the exit boundary is the image nodal point N’.
We can therefore consider that O and S (as well as O and S ) merge if the thic-
2
1
kness S S is small compared to the absolute value of the difference between
1 2
the radii of curvature’s algebraic R - R . The optical center O could then merge
2
1
with the vertices S and S ; the nodal points and principal points will also merge
1
2
with O. Good answer
Question 5-1
a. Try again.
b. You are mistaken, Try again.
c. Good answer, relation 5-6 from the course gives the same result.
d. Review your course.
e. You are confused.
Question 5-2.
a. Take your time.
b. Try again.
c. Good answer
d. Review your course.
e. You are confused.
Question 6 A lens is considered to be thin when its thickness is negligible in
relation to its face’s radii of curvature. The vertices can then merge into one
point S, and we can consider that O and S (as well as O and S ) merge if
2
1
the thickness S S is small compared to the absolute value of the difference
1 2
between the radii of curvature’s algebraic R - R . When those two conditions
2
1
are satisfied, the optical center O can merge with the vertices S and S ; the
1
2
nodal points and principal points will also merge with O. Very good, is can
see that you understand.

African Virtual University
Question 7: A thin lens is a centered system whose principal planes merge with
the optical center. This allows us to draw a scaled down representation of a
portion of straight line that is perpendicular to the lens’ principal axis. Very
good.
Question 8
a. Careful, it isn’t a converging lens.
b. Very good, such a lens is a diverging lens.
c. Think about it some more.
d. Carefully reread the question.
e. Take your time.
f. Very good, the vergency is negative since the lens is divergent.
g. Please try again.
Question 9: As is the case for all centered systems, a thin lens has an object fo-
cal length f and an image focal length f’. Since it is a centered system with
identical terminal media with indexes equal n , ‘THE’ focal length for the
0
lens is its image focal length that we will call . This focal length is related
to the through the equation:
1
⎛ 1
1 ⎞
⎛ 1
1 ⎞
V =
= (n − n )
(n n )
0
−
=
−
⎜
0
−
⎟
⎜⎜
⎟⎟
⎜
⎟
Φ
⎝ R
R
1
2 ⎠
⎝ S C
S C
1 1
2
2 ⎠
for a thin lens, which means that S and S merge with the optical center O.
1
2
Question 10: The expression that relates the vergency (optical power) V of a thin
lens allow us to see that two types of thin lenses can exist:
-
Converging thin lenses for which f’ is positive. The object focal point F
is in the object space and the image focal point F’ lies in the image space.
The two focal points are real. Excellent.
-
Diverging thin lenses for which f’ is negative and the focal points are vir-
tual. SC will be considered positive if the face is convex and negative
if the face si concave.


African Virtual University
(The annotations, where applicable must also be translated into English)
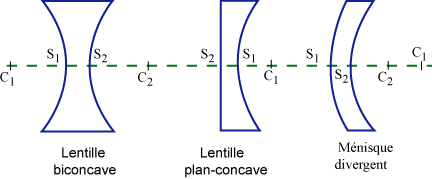
Therefore, the biconvex lens, convexe plane or meniscus that converge with
S C S
〈 C are converging lenses. Very good.
1 1
2
2
(The annotations, where applicable must also be translated into English)
On the other hand, the biconcave lens S C 〈0 , concave plane S C 〈0 or the
1
1
1
1
diverging meniscus S C S
〈 C are diverging lenses. Very good.
2
2
1 1
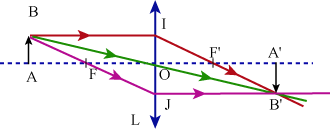
Question 11: Using the paraxial approximation (or Gauss approximation), the
image A’B’ of an object AB perpendicular to the axis is also perpendicular
to the axis. To find the image A’B’ of AB all we need to do is determine the
image B’ of B and then lower a perpendicular line to the axis the height of
B’ to find A’.


African Virtual University
To accomplish this we can use two of the rays that come from B:
-
the ray that intersects the optical center O and is not deviated.
-
the ray that intersects the lens’ object focal point F and emerges parallel
to the principal axis.
-
the ray that starts off parallel to the principal axis and intersects the image
focal point F’ as it emerges.
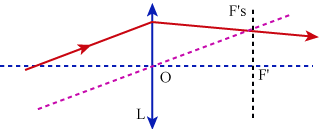
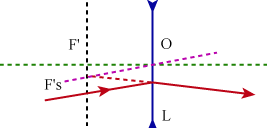
Question 12: We are looking for the point when the incident ray intersects the
object focal point F ; the emerging ray will run parallel to F O.
s
s
We draw a line parallel to the incident ray that intersects the optical center O and
intersects the image focal plane at F’ ; the ray exits the lens by intersecting the
s
secondary focal point F’ .
s
Feedback : Excellent commentary ; nice precise and clear sketches.

African Virtual University
Question 13-1.
a. Careful, the subject is a biconvex lens
b. Careful, we are talking about the image focal length.
c. Carefully reread the question.
d. Very good, the lens is biconvex and thus the image focal length is nega-
tive.
Question 13-2
a. Carefully reread the question.
b. Very good, the lens is biconvex and thus the image focal length is posi-
tive.
c. Careful, the subject is a biconvex lens
d. Careful, we are talking about the image focal length.
Question 14:
Conjugate relations for a central origin:
1
1
1
Using: p = OA
and
ʹ
p = OAʹ we get − + =
p pʹ f ʹ
A B
ʹ ʹ
OAʹ
pʹ
Magnification is described by: Γ =
=
=
AB
OA
p
Conjugate relations for a focal point origin:
Using: F A = x and F ʹAʹ = xʹ x.xʹ = − f ʹ2
f ʹ
xʹ
magnification is described by : Γ =
= −
x
f ʹ
(Which figure(s) are being referred to in this question?)
Feedback: Very good, the equations are correct.
Question 15-1
a. Think it through before answering.
b. Careful, the subject is the image plane not the object plane.
c. Good answer, the image plane’s position is indeed negative.
d. This is not the right answer. Try again.

African Virtual University
Question 15-2
The object principal plane’s position is described by S H and is equal to:
1
a. Great answer, you understand.
b. This is not quite the right value.
c.. Be careful, the distance is not negative.
d. Double-check your formula, this is not the right answer.
(Which figure(s) are being referred to in this question?)
Self Evaluation
The learners write down the difficulties they encountered while solving the pro-
blems. This will allow them to review the course sections they did not understand
as well and to prepare them for the summary evaluation.
Teacher Guidelines
The tutor will correct each group’s report and send out the appropriate feedback.
The answers will be posted on the ‘Student’ workspace. The grade received
from this activity is the same for each group member and accounts for 20% of
the module evaluation.


African Virtual University
Optional Educational Formative Evaluation
Activity Title
Rules for creating a short question.
Required Time
4 hours
Specific Objectives
To be able to:
•
Recall the three rules for creating a simple question;
•
Create a simple question using the three rules.
Applicable Reading
DIOUF, S. (2004). L’évaluation des apprentissages. UCAD of Dakar.
FASTEF(ex ENS). Unpublished course. (a more easily accessible reading
list is required)
Applicable Reading Justification
The text about evaluating what has been learned gives the reader information
on the questions relative to, the types and the functions of the evaluations, along
with the objectively corrected problems including short questions, the different
types of feedback, etc.
Activity Summary
For this activity, it is not necessary to complete the sentences. The goal is for
you to read the recommended text so that you may identify the rules for creating
certain questions like short (simple) questions.

African Virtual University
Formative Evaluation
1. Recall the rules for creating a simple question.
2. Which of the subsequent sentences follow those rules:
a. Some incident rays meet a boundary with an angle of incidence that is larger
than the critical angle and are therefore subject to …………………….
b. Some ………………… meet a boundary with an angle of incidence that
is larger than the critical angle and are therefore subject to total internal
reflection.
c. Some incident rays meet a boundary with an angle of incidence that is
…………………………………….. and are therefore subject to total
internal reflection.
Learning Activities
The learners read the recommended text while focusing on the part that is related
to the exercise. After three hours of reading, they answer the two questions. They
then write up an individual report and send it as an attachment in an e-mail to
the tutor for the course.
Answer Key
1. There are three rules for creating a short question.
The space to fill must not be at the beginning of a sentence.
The length of the space must not act as a hint to the answer.
The space to fill must always be at the end of a sentence.
2. Only sentence a obeys the rules.
Self Evaluation
This evaluation allows the learners to realize the difficulty in creating an evaluation
and to be aware of the way they should choose evaluation tools later on.
Teacher Guidelines
This evaluation is optional and is therefore not mandatory. Only those who wish
will complete it. The tutor will