Self-Study Guide 2: Programming in Fortran 95 by Dr. Rachael Padman - HTML preview

2 Good Programming Style

In section 1 we have covered some of the basics of programming. We will return to programming later when we look in even more detail at F95.

In this section we will briefly consider some rules for good practice in developing programs. When you come to tackle the computing exercise we will be looking for how you have tackled some of the issues we shall now discuss.

2.1 Readability

Your program should be as easy to follow in terms of its logical structure as possible. There are a number of ways we have already met that help us do this. Let us recap some of them.

First use comments. A general rule for comments is that you should use a comment when the F95 statements you write are not self explanatory. There is no need, for example, to add comments to obvious computational expressions. However you may want to add comments to the top of a block of expressions explaining how the following code relates to the physical problem.

• Similarly if you have a loop, a comment of the form below is of no help:

! loop from 1 to 10

do i=1,10

• But a comment of the following form, say in a program calculating a binomial might be very useful:

! loop to calculate nCr

do k=1,r

So use comments sensibly to make the code understandable.

• What we don’t want to hear is:

“I have written my program, now I just need to comment it before handing it in”

This is bad practice because comments are part of the program and should be there as much to help you follow your own intentions in programming as for the head of class to follow it.

• Another aspect of readability is indenting code blocks between do loops and in if clauses. This is very good practice. It uses the layout of the program to show at a glance the logical structure. Our strong advice is to make good use of indenting. Again it helps as much in program development as it does in presenting the final program.

2.2 Self-checking code

We have already seen in some of the examples how we can use checks to avoid numerical errors. There are a number of numerical operations which are “poorly defined”. These include, among many others:

a) division by zero

b) taking the square root or logarithm of a negative real number

Alternatively we may know the range of possible allowed values for a variable and can include checks to make sure this is not violated.

Sometimes we can be sure that variables cannot take on illegal values, other times we cannot. For example values may be supplied to the program by a user and the values may be wrong. Alternatively we may know that under certain conditions a variable may, for example, become negative and all this really means is that it should be set equal to zero; in fact the formula we are computing may explicitly state something like:

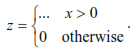
In either case you must be careful to check arguments to make sure they are “in range”. We have seen examples of this already and you should go back now and revise these methods.

Once again it is essential in program design to be sensible. Do not check a variable if it cannot be out of range; this just slows your code down. For example the following would be bad programming style:

real :: x

[some statements]

x = sin(y) +  1.0

if (x >= 0.0) z = sqrt(x)

Here x can never be less than zero; the test is not wrong, but clearly unnecessary and indicates a poor appreciation of the logic of the program.

2.3 Write clear code that relates to the physics

We are not aiming in this course to develop ultra-efficient programs or the shortest possible program etc. Our aim is for you to learn the basics of computational physics. Therefore you should aim to write your code so that it relates as clearly as possible to the physics and computational physics algorithms you are using as possible. You can split long expressions over many lines, for example, by using the continuation marker.

If the last character of a line is an ampersand ‘&’, then it is as if the next line was joined onto the current one (with the ‘&’ removed). Use this to lay out long expressions as clearly as possible.

• Another technique is to split long expressions using intermediate calculations. A simple example would be replacing something like:

res = sqrt(a + b*x + c*x*x + d*x*x*x) + &

log(e * f / (2.345*h + b*x))

with

t1 = a + b*x + c*x*x + d*x*x*x

t2 = E * F / (2.345*h + b*x)

res = sqrt(t1) + log(t2)

• Think about the choice of variable names. You can make the variable names very clear with names such as energy or momentum. This can be very helpful, but also cumbersome in long expressions. A useful rule of thumb is that if there is an accepted symbol for a physical quantity consider using that (e.g. E and p); use longer more descriptive names if one does not exist.

We will return to the topic of programming style later when we consider how the program can be broken up into smaller units. This will be the main job in the next section of the course.