Chapter 12
Arrays
An array is a set of values where each value is identified by an index. You
can make an array of ints, doubles, or any other type, but all the values in
an array have to have the same type.
Syntactically, array types look like other Java types except they are followed
by []. For example, int[] is the type “array of integers” and double[] is
the type “array of doubles.”
You can declare variables with these types in the usual ways:
int[] count;
double[] values;
Until you initialize these variables, they are set to null. To create the array
itself, use new.
count = new int[4];
values = new double[size];
The first assignment makes count refer to an array of 4 integers; the second
makes values refer to an array of doubles. The number of elements in
values depends on size. You can use any integer expression as an array
size.
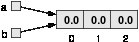
The following figure shows how arrays are represented in state diagrams:

150
Chapter 12. Arrays
The large numbers inside the boxes are the elements of the array. The small
numbers outside the boxes are the indices used to identify each box. When
you allocate an array if ints, the elements are initialized to zero.
12.1
Accessing elements
To store values in the array, use the [] operator. For example count[0]
refers to the “zeroeth” element of the array, and count[1] refers to the
“oneth” element. You can use the [] operator anywhere in an expression:
count[0] = 7;
count[1] = count[0] * 2;
count[2]++;
count[3] -= 60;
These are all legal assignment statements. Here is the result of this code
fragment:
The elements of the array are numbered from 0 to 3, which means that there
is no element with the index 4. This should sound familiar, since we saw the
same thing with String indices. Nevertheless, it is a common error to go be-
yond the bounds of an array, which throws an ArrayOutOfBoundsException.
You can use any expression as an index, as long as it has type int. One
of the most common ways to index an array is with a loop variable. For
example:
int i = 0;
while (i < 4) {
System.out.println(count[i]);
i++;
}
This is a standard while loop that counts from 0 up to 4, and when the loop
variable i is 4, the condition fails and the loop terminates. Thus, the body
of the loop is only executed when i is 0, 1, 2 and 3.
12.2. Copying arrays
151
Each time through the loop we use i as an index into the array, printing the
ith element. This type of array traversal is very common.
12.2
Copying arrays
When you copy an array variable, remember that you are copying a reference
to the array. For example:
double[] a = new double [3];
double[] b = a;
This code creates one array of three doubles, and sets two different variables
to refer to it. This situation is a form of aliasing.
Any changes in either array will be reflected in the other. This is not usually
the behavior you want; more often you want to allocate a new array and
copy elements from one to the other.
double[] b = new double [3];
int i = 0;
while (i < 4) {
b[i] = a[i];
i++;
}
12.3
for loops
The loops we have written have a number of elements in common. All of them
start by initializing a variable; they have a test, or condition, that depends
on that variable; and inside the loop they do something to that variable, like
increment it.
This type of loop is so common that there is another loop statement, called
for, that expresses it more concisely. The general syntax looks like this:
152
Chapter 12. Arrays
for (INITIALIZER; CONDITION; INCREMENTOR) {
BODY
}
This statement is equivalent to
INITIALIZER;
while (CONDITION) {
BODY
INCREMENTOR
}
except that it is more concise and, since it puts all the loop-related statements
in one place, it is easier to read. For example:
for (int i = 0; i < 4; i++) {
System.out.println(count[i]);
}
is equivalent to
int i = 0;
while (i < 4) {
System.out.println(count[i]);
i++;
}
Exercise 12.1. As an exercise, write a for loop to copy the elements of an
array.
12.4
Arrays and objects
In many ways, arrays behave like objects:
❼ When you declare an array variable, you get a reference to an array.
❼ You have to use new to create the array itself.
❼ When you pass an array as an argument, you pass a reference, which
means that the invoked method can change the contents of the array.
12.5. Array length
153
Some of the objects we looked at, like Rectangles, are similar to arrays in
the sense that they are collections of values. This raises the question, “How
is an array of 4 integers different from a Rectangle object?”
If you go back to the definition of “array” at the beginning of the chapter,
you see one difference: the elements of an array are identified by indices, and
the elements of an object have names.
Another difference is that the elements of an array have to be the same type.
Objects can have instance variables with different types.
12.5
Array length
Actually, arrays do have one named instance variable: length. Not surpris-
ingly, it contains the length of the array (number of elements). It is a good
idea to use this value as the upper bound of a loop, rather than a constant
value. That way, if the size of the array changes, you won’t have to go
through the program changing all the loops; they will work correctly for any
size array.
for (int i = 0; i < a.length; i++) {
b[i] = a[i];
}
The last time the body of the loop gets executed, i is a.length - 1, which
is the index of the last element. When i is equal to a.length, the condition
fails and the body is not executed, which is a good thing, since it would
throw an exception. This code assumes that the array b contains at least as
many elements as a.
Exercise 12.2. Write a method called cloneArray that takes an array of
integers as a parameter, creates a new array that is the same size, copies the
elements from the first array into the new one, and then returns a reference
to the new array.
12.6
Random numbers
Most computer programs do the same thing every time they are executed,
so they are said to be deterministic. Usually, determinism is a good thing,
154
Chapter 12. Arrays
since we expect the same calculation to yield the same result. But for some
applications we want the computer to be unpredictable. Games are an obvi-
ous example, but there are more.
Making a program truly nondeterministic turns out to be not so easy, but
there are ways to make it at least seem nondeterministic. One of them is
to generate random numbers and use them to determine the outcome of the
program. Java provides a method that generates pseudorandom numbers,
which may not be truly random, but for our purposes, they will do.
Check out the documentation of the random method in the Math class. The
return value is a double between 0.0 and 1.0. To be precise, it is greater
than or equal to 0.0 and strictly less than 1.0. Each time you invoke random
you get the next number in a pseudorandom sequence. To see a sample, run
this loop:
for (int i = 0; i < 10; i++) {
double x = Math.random();
System.out.println(x);
}
To generate a random double between 0.0 and an upper bound like high,
you can multiply x by high. How would you generate a random number
between low and high? How would you generate a random integer?
Exercise 12.3. Write a method called randomDouble that takes two doubles,
low and high, and that returns a random double x so that low ≤ x < high.
Exercise 12.4. Write a method called randomInt that takes two arguments,
low and high, and that returns a random integer between low and high, not
including high.
12.7
Array of random numbers
If your implementation of randomInt is correct, then every value in the range
from low to high-1 should have the same probability. If you generate a long
series of numbers, every value should appear, at least approximately, the
same number of times.
One way to test your method is to generate a large number of random values,
store them in an array, and count the number of times each value occurs.
12.7. Array of random numbers
155
The following method takes a single argument, the size of the array.
It
allocates a new array of integers, fills it with random values, and returns a
reference to the new array.
public static int[] randomArray(int n) {
int[] a = new int[n];
for (int i = 0; i<a.length; i++) {
a[i] = randomInt(0, 100);
}
return a;
}
The return type is int[], which means that this method returns an array of
integers. To test this method, it is convenient to have a method that prints
the contents of an array.
public static void printArray(int[] a) {
for (int i = 0; i<a.length; i++) {
System.out.println(a[i]);
}
}
The following code generates an array and prints it:
int numValues = 8;
int[] array = randomArray(numValues);
printArray(array);
On my machine the output is
27
6
54
62
54
2
44
81
which is pretty random-looking. Your results may differ.
If these were exam scores (and they would be pretty bad exam scores) the
teacher might present the results to the class in the form of a histogram,
156
Chapter 12. Arrays
which is a set of counters that keeps track of the number of times each value
appears.
For exam scores, we might have ten counters to keep track of how many
students scored in the 90s, the 80s, etc. The next few sections develop code
to generate a histogram.
12.8
Counting
A good approach to problems like this is to think of simple methods that
are easy to write, then combine them into a solution.
This process is
called bottom-up development. See http://en.wikipedia.org/wiki/
Top-down_and_bottom-up_design.
It is not always obvious where to start, but a good approach is to look for
subproblems that fit a pattern you have seen before.
In Section 8.7 we saw a loop that traversed a string and counted the number
of times a given letter appeared. You can think of this program as an example
of a pattern called “traverse and count.” The elements of this pattern are:
❼ A set or container that can be traversed, like an array or a string.
❼ A test that you can apply to each element in the container.
❼ A counter that keeps track of how many elements pass the test.
In this case, the container is an array of integers. The test is whether or not
a given score falls in a given range of values.
Here is a method called inRange that counts the number of elements in
an array that fall in a given range. The parameters are the array and two
integers that specify the lower and upper bounds of the range.
public static int inRange(int[] a, int low, int high) {
int count = 0;
for (int i=0; i<a.length; i++) {
if (a[i] >= low && a[i] < high) count++;
}
return count;
}
12.9. The histogram
157
I wasn’t specific about whether something equal to low or high falls in the
range, but you can see from the code that low is in and high is out. That
keeps us from counting any elements twice.
Now we can count the number of scores in the ranges we are interested in:
int[] scores = randomArray(30);
int a = inRange(scores, 90, 100);
int b = inRange(scores, 80, 90);
int c = inRange(scores, 70, 80);
int d = inRange(scores, 60, 70);
int f = inRange(scores, 0, 60);
12.9
The histogram
This code is repetitious, but it is acceptable as long as the number of ranges
is small. But imagine that we want to keep track of the number of times
each score appears, all 100 possible values. Would you want to write this?
int count0 = inRange(scores, 0, 1);
int count1 = inRange(scores, 1, 2);
int count2 = inRange(scores, 2, 3);
...
int count3 = inRange(scores, 99, 100);
I don’t think so. What we really want is a way to store 100 integers, prefer-
ably so we can use an index to access each one. Hint: array.
The counting pattern is the same whether we use a single counter or an array
of counters. In this case, we initialize the array outside the loop; then, inside
the loop, we invoke inRange and store the result:
int[] counts = new int[100];
for (int i = 0; i < counts.length; i++) {
counts[i] = inRange(scores, i, i+1);
}
The only tricky thing here is that we are using the loop variable in two roles:
as in index into the array, and as the parameter to inRange.
158
Chapter 12. Arrays
12.10
A single-pass solution
This code works, but it is not as efficient as it could be. Every time it invokes
inRange, it traverses the entire array. As the number of ranges increases,
that gets to be a lot of traversals.
It would be better to make a single pass through the array, and for each value,
compute which range it falls in. Then we could increment the appropriate
counter. In this example, that computation is trivial, because we can use the
value itself as an index into the array of counters.
Here is code that traverses an array of scores, once, and generates a his-
togram.
int[] counts = new int[100];
for (int i = 0; i < scores.length; i++) {
int index = scores[i];
counts[index]++;
}
Exercise 12.5. Encapsulate this code in a method called makeHist that takes
an array of scores and returns a histogram of the values in the array.
12.11
Glossary
array: A collection of values, where all the values have the same type, and
each value is identified by an index.
element: One of the values in an array. The [] operator selects elements.
index: An integer variable or value used to indicate an element of an array.
deterministic: A program that does the same thing every time it is invoked.
pseudorandom: A sequence of numbers that appear to be random, but
which are actually the product of a deterministic computation.
histogram: An array of integers where each integer counts the number of
values that fall into a certain range.
12.12. Exercises
159
12.12
Exercises
Exercise 12.6. Write a method named areFactors that takes an integer n
and an array of integers, and that returns true if the numbers in the array
are all factors of n (which is to say that n is divisible by all of them). HINT:
See Exercise 6.1.
Exercise 12.7. Write a method that takes an array of integers and an integer
named target as arguments, and that returns the first index where target
appears in the array, if it does, and -1 otherwise.
Exercise 12.8. Some programmers disagree with the general rule that vari-
ables and methods should be given meaningful names. Instead, they think
variables and methods should be named after fruit.
For each of the following methods, write one sentence that describes abstractly
what the method does. For each variable, identify the role it plays.
public static int banana(int[] a) {
int grape = 0;
int i = 0;
while (i < a.length) {
grape = grape + a[i];
i++;
}
return grape;
}
public static int apple(int[] a, int p) {
int i = 0;
int pear = 0;
while (i < a.length) {
if (a[i] == p) pear++;
i++;
}
return pear;
}
public static int grapefruit(int[] a, int p) {
for (int i = 0; i<a.length; i++) {
if (a[i] == p) return i;
160
Chapter 12. Arrays
}
return -1;
}
The purpose of this exercise is to practice reading code and recognizing the
computation patterns we have seen.
Exercise 12.9.
1. What is the output of the following program?
2. Draw a stack diagram that shows the state of the program just before
mus returns.
3. Describe in a few words what mus does.
public static int[] make(int n) {
int[] a = new int[n];
for (int i=0; i<n; i++) {
a[i] = i+1;
}
return a;
}
public static void dub(int[] jub) {
for (int i=0; i<jub.length; i++) {
jub[i] *= 2;
}
}
public static int mus(int[] zoo) {
int fus = 0;
for (int i=0; i<zoo.length; i++) {
fus = fus + zoo[i];
}
return fus;
}
public static void main(String[] args) {
int[] bob = make(5);
dub(bob);
12.12. Exercises
161
System.out.println(mus(bob));
}
Exercise 12.10. Many of the patterns we have seen for traversing arrays
can also be written recursively. It is not common to do so, but it is a useful
exercise.
1. Write a method called maxInRange that takes an array of integers
and a range of indices (lowIndex and highIndex), and that finds the
maximum value in the array, considering only the elements between
lowIndex and highIndex, including both ends.
This method should be recursive. If the length of the range is 1, that is,
if lowIndex == highIndex, we know immediately that the sole element
in the range must be the maximum. So that’s the base case.
If there is more than one element in the range, we can break the array
into two pieces, find the maximum in each of the pieces, and then find
the maximum of the maxima.
2. Methods like maxInRange can be awkward to use. To find the largest
element in an array, we have to provide a range that includes the entire
array.
double max = maxInRange(array, 0, a.length-1);
Write a method called max that takes an array as a parameter and that
uses maxInRange to find and return the largest value. Methods like max
are sometimes called wrapper methods because they provide a layer
of abstraction around an awkward method and make it easier to use.
The method that actually performs the computation is called the helper
method.
3. Write a recursive version of find using the wrapper-helper pattern.
find should take an array of integers and a target integer. It should
return the index of the first location where the target integer appears in
the array, or -1 if it does not appear.
Exercise 12.11. One not-very-efficient way to sort the elements of an array
is to find the largest element and swap it with the first element, then find
the second-largest element and swap it with the second, and so on. This
162
Chapter 12. Arrays
method is called a selection sort (see http: // en. wikipedia. org/ wiki/
Selection_ sort ).
1. Write a method called indexOfMaxInRange that takes an array of inte-
gers, finds the largest element in the given range, and returns its index.
You can modify your recursive version of maxInRange or you can write
an iterative version from scratch.
2. Write a method called swapElement that takes an array of integers and
two indices, and that swaps the elements at the given indices.
3. Write a method called selectionSort that takes an array of integers
and that uses indexOfMaxInRange and swapElement to sort the array
from largest to smallest.
Exercise 12.12. Write a method called letterHist that takes a String as
a parameter and that returns a histogram of the letters in the String. The
zeroeth element of the histogram should contain the number of a’s in the
String (upper and lower case); the 25th element should contain the number
of z’s. Your solution should only traverse the String once.
Exercise 12.13. A word is said to be a “doubloon” if every letter that appears
in the word appears exactly twice. For example, the following are all the
doubloons I found in my dictionary.
Abba, Anna, appall, appearer, appeases, arraigning, beriberi, bil-
abial, boob, Caucasus, coco, Dada, deed, Emmett, Hannah, horse-
shoer, intestines, Isis, mama, Mimi, murmur, noon, Otto, papa,
peep, reappear, redder, sees, Shanghaiings, Toto
Write a method called isDoubloon that returns true if the given word is a
doubloon and false otherwise.
Exercise 12.14. Two words are anagrams if they contain the same letters
(and the same number of each letter). For example, “stop” is an anagram of
“pots” and “allen downey” is an anagram of “well annoyed.”
Write a method that takes two Strings and returns true if the Strings are
anagrams of each other.
Optional challenge: read the letters of the Strings only once.
12.12. Exercises
163
Exercise 12.15. In Scrabble each player has a set of tiles with letters on
them, and the object of the game is to use those letters to spell words. The
scoring system is complicated, but longer words are usually worth more than
shorter words.
Imagine you are given your set of tiles as a String, like "quijibo" and you
are given another String to test, like "jib". Write a method called canSpell
that takes two Strings and returns true if the set of tiles can be used to spell
the word. You might have more than one tile with the same letter, but you
can only use each tile once.
Optional challenge: read the letters of the Strings only once.
Exercise 12.16. In real Scrabble, there are some blank tiles that can be used
as wild cards; that is, a blank tile can be used to represent any letter.
Think of an algorithm for canSpell that deals with wild cards. Don’t get
bogged down in details of implementation like how to represent wild cards.
Just describe the algorithm, using English, pseudocode, or Java.
164
Chapter 12. Arrays





