Chapter 13
Arrays of Objects
13.1
The Road Ahead
In the next three chapters we will develop programs to work with playing
cards and decks of cards. Before we dive in, here is an outline of the steps:
1. In this chapter we’ll define a Card class and write methods that work
with Cards and arrays of Cards.
2. In Chapter 14 we will create a Deck class and write methods that
operate on Decks.
3. In Chapter 15 I will present object-oriented programming (OOP) and
we will transform the Card and Deck classes into a more OOP style.
I think that way of proceeding makes the road smoother; the drawback is
that we will see several versions of the same code, which can be confusing.
If it helps, you can download the code for each chapter as you go along. The
code for this chapter is here: http://thinkapjava.com/code/Card1.java.
13.2
Card objects
If you are not familiar with common playing cards, now would be a good
time to get a deck, or else this chapter might not make much sense. Or read
http://en.wikipedia.org/wiki/Playing_card.
166
Chapter 13. Arrays of Objects
There are 52 cards in a deck; each belongs to one of four suits and one of
13 ranks. The suits are Spades, Hearts, Diamonds and Clubs (in descending
order in Bridge). The ranks are Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen and
King. Depending on what game you are playing, the Ace may be considered
higher than King or lower than 2.
If we want to define a new object to represent a playing card, it is pretty
obvious what the instance variables should be: rank and suit. It is not
as obvious what type the instance variables should be. One possibility is
Strings, containing things like "Spade" for suits and "Queen" for ranks. One problem with this implementation is that it would not be easy to compare
cards to see which had higher rank or suit.
An alternative is to use integers to encode the ranks and suits. By “encode,”
I do not mean what some people think, which is to encrypt, or translate into
a secret code. What a computer scientist means by “encode” is something
like “define a mapping between a sequence of numbers and the things I want
to represent.” For example,
Spades
→
3
Hearts
→
2
Diamonds
→
1
Clubs
→
0
The obvious feature of this mapping is that the suits map to integers in order,
so we can compare suits by comparing integers. The mapping for ranks is
fairly obvious; each of the numerical ranks maps to the corresponding integer,
and for face cards:
Jack
→
11
Queen
→
12
King
→
13
The reason I am using mathematical notation for these mappings is that they
are not part of the program. They are part of the program design, but they
never appear explicitly in the code. The class definition for the Card type
looks like this:
class Card
{
int suit, rank;
13.3. The printCard method
167
public Card() {
this.suit = 0;
this.rank = 0;
}
public Card(int suit, int rank) {
this.suit = suit;
this.rank = rank;
}
}
As usual, I provide two constructors: one takes a parameter for each instance
variable; the other takes no parameters.
To create an object that represents the 3 of Clubs, we invoke new:
Card threeOfClubs = new Card(0, 3);
The first argument, 0 represents the suit Clubs.
13.3
The printCard method
When you create a new class, the first step is to declare the instance variables
and write constructors. The second step is to write the standard methods
that every object should have, including one that prints the object, and one
or two that compare objects. Let’s start with printCard.
To print Card objects in a way that humans can read easily, we want to map
the integer codes onto words. A natural way to do that is with an array of
Strings. You can create an array of Strings the same way you create an
array of primitive types:
String[] suits = new String [4];
Then we can set the values of the elements of the array.
suits[0] = "Clubs";
suits[1] = "Diamonds";
suits[2] = "Hearts";
suits[3] = "Spades";
Creating an array and initializing the elements is such a common operation
that Java provides a special syntax for it:
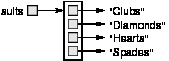
168
Chapter 13. Arrays of Objects
String[] suits = { "Clubs", "Diamonds", "Hearts", "Spades" }; This statement is equivalent to the separate declaration, allocation, and assignment. The state diagram of this array looks like:
The elements of the array are references to the Strings, rather than Strings
themselves.
Now we need another array of Strings to decode the ranks:
String[] ranks = { "narf", "Ace", "2", "3", "4", "5", "6",
"7", "8", "9", "10", "Jack", "Queen", "King" }; The reason for the "narf" is to act as a place-keeper for the zeroeth element
of the array, which is never used (or shouldn’t be). The only valid ranks
are 1–13. To avoid this wasted element, we could have started at 0, but the
mapping is more natural if we encode 2 as 2, and 3 as 3, etc.
Using these arrays, we can select the appropriate Strings by using the suit
and rank as indices. In the method printCard,
public static void printCard(Card c) {
String[] suits = { "Clubs", "Diamonds", "Hearts", "Spades" }; String[] ranks = { "narf", "Ace", "2", "3", "4", "5", "6",
"7", "8", "9", "10", "Jack", "Queen", "King" }; System.out.println(ranks[c.rank] + " of " + suits[c.suit]);
}
the expression suits[c.suit] means “use the instance variable suit from
the object c as an index into the array named suits, and select the appro-
priate string.” The output of this code
Card card = new Card(1, 11);
printCard(card);
is Jack of Diamonds.
13.4. The sameCard method
169
13.4
The sameCard method
The word “same” is one of those things that occur in natural language that
seem perfectly clear until you give it some thought, and then you realize
there is more to it than you expected.
For example, if I say “Chris and I have the same car,” I mean that his car and
mine are the same make and model, but they are two different cars. If I say
“Chris and I have the same mother,” I mean that his mother and mine are
one person. So the idea of “sameness” is different depending on the context.
When you talk about objects, there is a similar ambiguity. For example, if
two Cards are the same, does that mean they contain the same data (rank
and suit), or they are actually the same Card object?
To see if two references refer to the same object, we use the == operator. For
example:
Card card1 = new Card(1, 11);
Card card2 = card1;
if (card1 == card2) {
System.out.println("card1 and card2 are identical.");
}
References to the same object are identical. References to objects with same
data are equivalent.
To check equivalence, it is common to write a method with a name like
sameCard.
public static boolean sameCard(Card c1, Card c2) {
return(c1.suit == c2.suit && c1.rank == c2.rank);
}
Here is an example that creates two objects with the same data, and uses
sameCard to see if they are equivalent:
Card card1 = new Card(1, 11);
Card card2 = new Card(1, 11);
if (sameCard(card1, card2)) {
System.out.println("card1 and card2 are equivalent.");
}
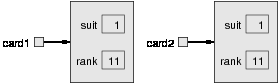
170
Chapter 13. Arrays of Objects
If references are identical, they are also equivalent, but if they are equivalent,
they are not necessarily identical.
In this case, card1 and card2 are equivalent but not identical, so the state
diagram looks like this:
What does it look like when card1 and card2 are identical?
In Section 8.10 I said that you should not use the == operator on Strings
because it does not do what you expect. Instead of comparing the contents
of the String (equivalence), it checks whether the two Strings are the same
object (identity).
13.5
The compareCard method
For primitive types, the conditional operators compare values and determine
when one is greater or less than another. These operators (< and > and the
others) don’t work for object types. For Strings Java provides a compareTo
method. For Cards we have to write our own, which we will call compareCard.
Later, we will use this method to sort a deck of cards.
Some sets are completely ordered, which means that you can compare any
two elements and tell which is bigger. Integers and floating-point numbers
are totally ordered. Some sets are unordered, which means that there is no
meaningful way to say that one element is bigger than another. Fruits are
unordered, which is why we cannot compare apples and oranges. In Java, the
boolean type is unordered; we cannot say that true is greater than false.
The set of playing cards is partially ordered, which means that sometimes
we can compare cards and sometimes not. For example, I know that the 3
of Clubs is higher than the 2 of Clubs, and the 3 of Diamonds is higher than
13.6. Arrays of cards
171
the 3 of Clubs. But which is better, the 3 of Clubs or the 2 of Diamonds?
One has a higher rank, but the other has a higher suit.
To make cards comparable, we have to decide which is more important, rank
or suit. The choice is arbitrary, but when you buy a new deck of cards, it
comes sorted with all the Clubs together, followed by all the Diamonds, and
so on. So let’s say that suit is more important.
With that decided, we can write compareCard. It takes two Cards as param-
eters and return 1 if the first card wins, -1 if the second card wins, and 0 if
they are equivalent.
First we compare suits:
if (c1.suit > c2.suit) return 1;
if (c1.suit < c2.suit) return -1;
If neither statement is true, the suits must be equal, and we have to compare
ranks:
if (c1.rank > c2.rank) return 1;
if (c1.rank < c2.rank) return -1;
If neither of these is true, the ranks must be equal, so we return 0.
Exercise 13.1. Encapsulate this code in a method. Then modify it so that
aces are ranked higher than Kings.
13.6
Arrays of cards
By now we have seen several examples of composition (the ability to combine
language features in a variety of arrangements). One of the first examples
we saw was using a method invocation as part of an expression. Another
example is the nested structure of statements: you can put an if statement
within a while loop, or within another if statement, etc.
Having seen this pattern, and having learned about arrays and objects, you
should not be surprised to learn that you can make arrays of objects. And
you can define objects with arrays as instance variables; you can make arrays
that contain arrays; you can define objects that contain objects, and so on.
In the next two chapters we will see examples of these combinations using
Card objects.
This example creates an array of 52 cards:
172
Chapter 13. Arrays of Objects
Card[] cards = new Card [52];
Here is the state diagram for this object:
0 1 2 3
51
cards
The array contains references to objects; it does not contain the Card objects
themselves. The elements are initialized to null. You can access the elements
of the array in the usual way:
if (cards[0] == null) {
System.out.println("No cards yet!");
}
But if you try to access the instance variables of the non-existent Cards, you
get a NullPointerException.
cards[0].rank;
// NullPointerException
But that is the correct syntax for accessing the rank of the “zeroeth” card
in the deck. This is another example of composition, combining the syntax
for accessing an element of an array and an instance variable of an object.
The easiest way to populate the deck with Card objects is to write a nested
loop:
int index = 0;
for (int suit = 0; suit <= 3; suit++) {
for (int rank = 1; rank <= 13; rank++) {
cards[index] = new Card(suit, rank);
index++;
}
}
The outer loop enumerates the suits from 0 to 3. For each suit, the inner
loop enumerates the ranks from 1 to 13. Since the outer loop runs 4 times,
and the inner loop runs 13 times, the body is executed is 52 times.
I used index to keep track of where in the deck the next card should go.
The following state diagram shows what the deck looks like after the first
two cards have been allocated:
13.7. The printDeck method
173
0 1 2 3
51
cards
suit
0
suit
0
rank
1
rank
2
Exercise 13.2. Encapsulate this deck-building code in a method called
makeDeck that takes no parameters and returns a fully-populated array of
Cards.
13.7
The printDeck method
When you work with arrays, it is convenient to have a method that prints
the contents. We have seen the pattern for traversing an array several times,
so the following method should be familiar:
public static void printDeck(Card[] cards) {
for (int i=0; i < cards.length; i++) {
printCard(cards[i]);
}
}
Since cards has type Card[], an element of cards has type Card.
So
cards[i] is a legal argument for printCard.
13.8
Searching
The next method I’ll write is findCard, which searches an array of Cards to
see whether it contains a certain card. This method gives me a chance to
demonstrate two algorithms: linear search and bisection search.
Linear search is pretty obvious; we traverse the deck and compare each card
to the one we are looking for. If we find it we return the index where the
card appears. If it is not in the deck, we return -1.
174
Chapter 13. Arrays of Objects
public static int findCard(Card[] cards, Card card) {
for (int i = 0; i< cards.length; i++) {
if (sameCard(cards[i], card)) {
return i;
}
}
return -1;
}
The arguments of findCard are card and cards. It might seem odd to have
a variable with the same name as a type (the card variable has type Card).
We can tell the difference because the variable begins with a lower-case letter.
The method returns as soon as it discovers the card, which means that we
do not have to traverse the entire deck if we find the card we are looking for.
If we get to the end of the loop, we know the card is not in the deck.
If the cards in the deck are not in order, there is no way to search faster than
this. We have to look at every card because otherwise we can’t be certain
the card we want is not there.
But when you look for a word in a dictionary, you don’t search linearly
through every word, because the words are in alphabetical order. As a result,
you probably use an algorithm similar to a bisection search:
1. Start in the middle somewhere.
2. Choose a word on the page and compare it to the word you are looking
for.
3. If you find the word you are looking for, stop.
4. If the word you are looking for comes after the word on the page, flip
to somewhere later in the dictionary and go to step 2.
5. If the word you are looking for comes before the word on the page, flip
to somewhere earlier in the dictionary and go to step 2.
If you ever get to the point where there are two adjacent words on the page
and your word comes between them, you can conclude that your word is not
in the dictionary.
13.8. Searching
175
Getting back to the deck of cards, if we know the cards are in order, we can
write a faster version of findCard. The best way to write a bisection search
is with a recursive method, because bisection is naturally recursive.
The trick is to write a method called findBisect that takes two indices as
parameters, low and high, indicating the segment of the array that should
be searched (including both low and high).
1. To search the array, choose an index between low and high (call it mid)
and compare it to the card you are looking for.
2. If you found it, stop.
3. If the card at mid is higher than your card, search the range from low
to mid-1.
4. If the card at mid is lower than your card, search the range from mid+1
to high.
Steps 3 and 4 look suspiciously like recursive invocations. Here’s what this
looks like translated into Java code:
public static int findBisect(Card[] cards, Card card, int low, int high) {
// TODO: need a base case
int mid = (high + low) / 2;
int comp = compareCard(cards[mid], card);
if (comp == 0) {
return mid;
} else if (comp > 0) {
return findBisect(cards, card, low, mid-1);
} else {
return findBisect(cards, card, mid+1, high);
}
}
This code contains the kernel of a bisection search, but it is still missing a
piece, which is why I added a TODO comment.
As written, the method recurses forever if the card is not in the deck. We
need a base case to handle this condition.
176
Chapter 13. Arrays of Objects
If high is less than low, there are no cards between them, see we conclude
that the card is not in the deck. If we handle that case, the method works
correctly:
public static int findBisect(Card[] cards, Card card, int low, int high) {
System.out.println(low + ", " + high);
if (high < low) return -1;
int mid = (high + low) / 2;
int comp = compareCard(cards[mid], card);
if (comp == 0) {
return mid;
} else if (comp > 0) {
return findBisect(cards, card, low, mid-1);
} else {
return findBisect(cards, card, mid+1, high);
}
}
I added a print statement so I can follow the sequence of recursive invocations.
I tried out the following code:
Card card1 = new Card(1, 11);
System.out.println(findBisect(cards, card1, 0, 51));
And got the following output:
0, 51
0, 24
13, 24
19, 24
22, 24
23
Then I made up a card that is not in the deck (the 15 of Diamonds), and
tried to find it. I got the following:
0, 51
0, 24
13, 24
13.9. Decks and subdecks
177
13, 17
13, 14
13, 12
-1
These tests don’t prove that this program is correct. In fact, no amount of
testing can prove that a program is correct. On the other hand, by looking at
a few cases and examining the code, you might be able to convince yourself.
The number of recursive invocations is typically 6 or 7, so we only invoke
compareCard 6 or 7 times, compared to up to 52 times if we did a linear
search. In general, bisection is much faster than a linear search, and even
more so for large arrays.
Two common errors in recusive programs are forgetting to include a base case
and writing the recursive call so that the base case is never reached. Either
error causes infinite recursion, which throws a StackOverflowException.
13.9
Decks and subdecks
Here is the prototype of findBisect:
public static int findBisect(Card[] deck, Card card, int low, int high)
We can think of cards, low and high as a single parameter that specifies a
subdeck. This way of thinking is common, and I sometimes think of it as
an abstract parameter. What I mean by “abstract,” is something that is
not literally part of the program text, but which describes the function of
the program at a higher level.
For example, when you invoke a method and pass an array and the bounds
low and high, there is nothing that prevents the invoked method from ac-
cessing parts of the array that are out of bounds. So you are not literally
sending a subset of the deck; you are really sending the whole deck. But
as long as the recipient plays by the rules, it makes sense to think of it,
abstractly, as a subdeck.
This kind of thinking, in which a program takes on meaning beyond what is
literally encoded, is an important part of thinking like a computer scientist.
178
Chapter 13. Arrays of Objects
The word “abstract” gets used so often and in so many contexts that it comes
to lose its meaning. Nevertheless, abstraction is a central idea in computer
science (and many other fields).
A more general definition of “abstraction” is “The process of modeling a
complex system with a simplified description to suppress unnecessary details
while capturing relevant behavior.”
13.10
Glossary
encode: To represent one set of values using another set of values, by con-
structing a mapping between them.
identity: Equality of references. Two references that point to the same
object.
equivalence: Equality of values. Two references that point to objects that
contain the same data.
abstract parameter: A set of parameters that act together as a single pa-
rameter.
abstraction: The process of interpreting a program (or anything else) at a
higher level than what is literally represented by the code.
13.11
Exercises
Exercise 13.3. In Blackjack the object of the game is to get a collection of
cards with a score of 21. The score for a hand is the sum of scores for all
cards. The score for an aces is 1, for all face cards is ten, and for all other
cards the score is the same as the rank. Example: the hand (Ace, 10, Jack,
3) has a total score of 1 + 10 + 10 + 3 = 24.
Write a method called handScore that takes an array of cards as an argument
and that returns the total score.
Exercise 13.4. In Poker a “flush” is a hand that contains five or more cards
of the same suit. A hand can contain any number of cards.
13.11. Exercises
179
1. Write a method called suitHist that takes an array of Cards as a
parameter and that returns a histogram of the suits in the hand. Your
solution should only traverse the array once.
2. Write a method called hasFlush that takes an array of Cards as a
parameter and that returns true if the hand contains a flush, and false
otherwise.
Exercise 13.5. Working with cards is more interesting if you can display
them on the screen. If you haven’t played with the graphics examples in
Appendix A, you might want to do that now.
Then download http: // thinkapjava. com/ code/ CardTable. java and
http: // thinkapjava. com/ code/ cardset. zip .
<





