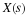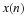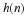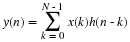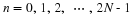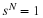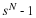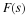A third approach to removing redundancy in an algorithm is to express the algorithm as an operator and then factor that operator into sparse factors. This approach is used by Tolimieri 4, 5, Egner 3, Selesnick, Elliott 2 and others. It is presented in a more general form in DFT and FFT: An Algebraic View The operators may be in the form of a matrix or a tensor operator.
The definition of the DFT in Multidimensional Index Mapping: Equation 1 can written as a matrix-vector operation by C=WX which, for N=8 is
which clearly requires N2=64 complex multiplications and N(N–1) additions.
A factorization of the DFT operator, W, gives 
and
or, expanded,
where the Fi matrices are sparse. Note that each has 16 (or 2N) non-zero terms and F2 and F3 have 8 (or N) non-unity terms. If N=2M, then the number of factors is log(N)=M. In another form with the twiddle factors separated so as to count the complex multiplications we have
which is in the form 
described by the index map.
A1, A2, and A3 each represents 8 additions, or, in general, N additions.
M1 and M2 each represent 4 (or N/2) multiplications.
This is a very interesting result showing that implementing the DFT using the factored form requires considerably less arithmetic than the single factor definition. Indeed, the form of the formula that Cooley and Tukey derived showing that the amount of arithmetic required by the FFT is on the order of Nlog(N) can be seen from the factored operator formulation.
Much of the theory of the FFT can be developed using operator factoring and it has some advantages for implementation of parallel and vector computer architectures. The eigenspace approach is somewhat of the same type 1.
A very general structure for all kinds of algorithms can be generalized from the approach of operators and operator decomposition. This is developed as “Algebraic Theory of Signal Processing" discussed in the module DFT and FFT: An Algebraic View by Püschel and others 3.
Beard, James K. (2003). The FFT in the 21st Century: Eigenspace Processing. Boston: Kluwer.
Elliott, Douglas F. (Ed.). (1987). Handbook of Digital Signal Processing. [Chapter 7 on FFT by Elliott]. San Diego, CA: Academic Press.
Egner, Sebastian and Püschel, Markus. (2001). Automatic Generation of Fast Discrete Signal Transforms. IEEE Transactions on Signal Processing, 49(9), 1992–202.
Tolimieri, Richard and An, Myoung and Lu, Chao. (1989, 1997). Algorithms for Discrete Fourier Transform and Convolution. (second). New York: Springer-Verlag.
Tolimieri, Richard and An, Myoung and Lu, Chao. (1993, 1997). Mathematics of Multidimensional Fourier Transform Algorithms. (second). New York: Springer-Verlag.