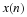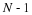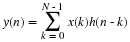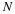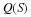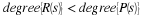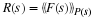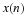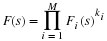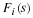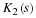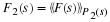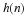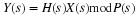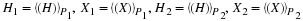In this section a method quite different from the index mapping or polynomial evaluation is developed. Rather than dealing with the DFT directly, it is converted into a cyclic convolution which must then be carried out by some efficient means. Those means will be covered later, but here the conversion will be explained. This method requires use of some number theory, which can be found in an accessible form in 12 or 13 and is easy enough to verify on one's own. A good general reference on number theory is 14.

The DFT and cyclic convolution are defined by

(5.1)

(5.2)

For both, the indices are evaluated modulo N. In order to convert the DFT in Equation 5.1 into the cyclic convolution of Equation 5.2, the nk product must be changed to the k–n difference. With real numbers, this can be done with logarithms, but it is more complicated when working in a finite set of integers modulo N. From number theory 1, 12, 13, 14, it can be shown that if the modulus is a prime number, a base (called a primitive root) exists such that a form of integer logarithm can be defined. This is stated in the following way. If N is a prime number, a number r called a primitive roots exists such that the integer equation

(5.3)

creates a unique, one-to-one map of the N–1 member set m={0,...,N–2} and the N–1 member set n={1,...,N–1}. This is because the multiplicative group of integers modulo a prime, p, is isomorphic to the additive group of integers modulo (p–1) and is illustrated for N=5 below.

Table 5.1. Table of Integers modulo 5, [* not defined]

r	m=	0	1	2	3	4	5	6	7
1		1	1	1	1	1	1	1	1
2		1	2	4	3	1	2	4	3
3		1	3	4	2	1	3	4	2
4		1	4	1	4	1	4	1	4
5		*	0	0	0	*	0	0	0
6		1	1	1	1	1	1	1	1

Table 5.1 is an array of values of r^m modulo N and it is easy to see that there are two primitive roots, 2 and 3, and Equation 5.3 defines a permutation of the integers n from the integers m (except for zero). Equation 5.3 and a primitive root (usually chosen to be the smallest of those that exist) can be used to convert the DFT in Equation 5.1 to the convolution in Equation 5.2. Since Equation 5.3 cannot give a zero, a new length-(N-1) data sequence is defined from x(n) by removing the term with index zero. Let

and

where the term with the negative exponent (the inverse) is defined as the integer that satisfies

(5.6)

If N is a prime number, r^–m always exists. For example, 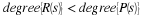. Equation 5.1 now becomes

(5.7)

for s=0,1,..,N–2, and

(5.8)

New functions are defined, which are simply a permutation in the order of the original functions, as

(5.9)

Equation 5.7 then becomes

(5.10)

which is cyclic convolution of length N-1 (plus x(0)) and is denoted as

Applying this change of variables (use of logarithms) to the DFT can best be illustrated from the matrix formulation of the DFT. Equation 5.1 is written for a length-5 DFT as

(5.12)

where the square matrix should contain the terms of W^nk but for clarity, only the exponents nk are shown. Separating the x(0) term, applying the mapping of Equation 5.9, and using the primitive roots r=2 (and r^–1=3) gives

(5.13)

and

which can be seen to be a reordering of the structure in Equation 5.12. This is in the form of cyclic convolution as indicated in Equation 5.10. Rader first showed this in 1968 12, stating that a prime length-N DFT could be converted into a length-(N-1) cyclic convolution of a permutation of the data with a permutation of the W's. He also stated that a slightly more complicated version of the same idea would work for a DFT with a length equal to an odd prime to a power. The details of that theory can be found in 12, 10.

Until 1976, this conversion approach received little attention since it seemed to offer few advantages. It has specialized applications in calculating the DFT if the cyclic convolution is done by distributed arithmetic table look-up 5 or by use of number theoretic transforms 1, 12, 13. It and the Goertzel algorithm 16, 3 are efficient when only a few DFT values need to be calculated. It may also have advantages when used with pipelined or vector hardware designed for fast inner products. One example is the TMS320 signal processing microprocessor which is pipelined for inner products. The general use of this scheme emerged when new fast cyclic convolution algorithms were developed by Winograd 21.

The DFT of x(n) evaluates the Z-transform of x(n) on N equally spaced points on the unit circle in the z plane. Using a nonlinear change of variables, one can create a structure which is equivalent to modulation and filtering x(n) by a “chirp" signal. 2, 20, 19, 16, 18, 3.

The mathematical identity (k–n)²=k²–2kn+n² gives

(5.15)

which substituted into the definition of the DFT in Multidimensional Index Mapping: Equation 1 gives

(5.16)

This equation can be interpreted as first multiplying (modulating) the data x(n) by a chirp sequence (W^n2/2, then convolving (filtering) it, then finally multiplying the filter output by the chirp sequence to give the DFT.

Define the chirp sequence or signal as h(n)=W^n2/2 which is called a chirp because the squared exponent gives a sinusoid with changing frequency. Using this definition, Equation 5.16 becomes

(5.17)

We know that convolution can be carried out by multiplying the DFTs of the signals, here we see that evaluation of the DFT can be carried out by convolution. Indeed, the convolution represented by * in Equation 5.17 can be carried out by DFTs (actually FFTs) of a larger length. This allows a prime length DFT to be calculated by a very efficient length-2^M FFT. This becomes practical for large N when a particular non-composite (or N with few factors) length is required.

As developed here, the chirp z-transform evaluates the z-transform at equally spaced points on the unit circle. A slight modification allows evaluation on a spiral and in segments 19, 16 and allows savings with only some input values are nonzero or when only some output values are needed. The story of the development of this transform is given in 18.

Two Matlab programs to calculate an arbitrary length DFT using the chirp z-transform is shown in screen.

function y = chirpc(x);
% function y = chirpc(x)
% computes an arbitrary-length DFT with the
% chirp z-transform algorithm.  csb.  6/12/91
%
N  = length(x);  n = 0:N-1;     %Sequence length
W  = exp(-j*pi*n.*n/N);         %Chirp signal
xw = x.*W;                      %Modulate with chirp
WW = [conj(W(N:-1:2)),conj(W)]; %Construct filter
y  = conv(WW,xw);               %Convolve w filter
y  = y(N:2*N-1).*W;             %Demodulate w chirp
 
 
function y = chirp(x);
% function y = chirp(x)
% computes an arbitrary-length Discrete Fourier Transform (DFT)
% with the chirp z transform algorithm. The linear convolution
% then required is done with FFTs.
% 1988: L. Arevalo; 11.06.91 K. Schwarz, LNT Erlangen; 6/12/91 csb.
%
N   = length(x);                %Sequence length
L   = 2^ceil(log((2*N-1))/log(2)); %FFT length
n   = 0:N-1;
W   = exp(-j*pi*n.*n/N);        %Chirp signal
FW  = fft([conj(W), zeros(1,L-2*N+1), conj(W(N:-1:2))],L);
y   = ifft(FW.*fft(x.'.*W,L));  %Convolve using FFT
y   = y(1:N).*W;                %Demodulate
 

Goertzel's algorithm 7, 3, 15 is another methods that calculates the DFT by converting it into a digital filtering problem. The method looks at the calculation of the DFT as the evaluation of a polynomial on the unit circle in the complex plane. This evaluation is done by Horner's method which is implemented recursively by an IIR filter.

The First-Order Goertzel Algorithm

The polynomial whose values on the unit circle are the DFT is a slightly modified z-transform of x(n) given by

(5.18)

which for clarity in this development uses a positive exponent . This is illustrated for a length-4 sequence as a third-order polynomial by

(5.19) X ( z ) = x ( 3