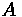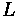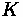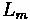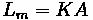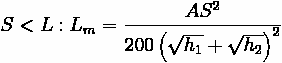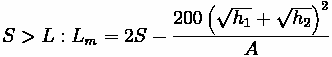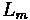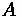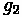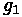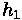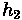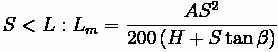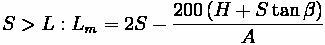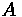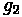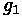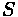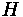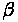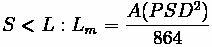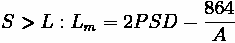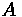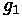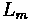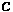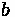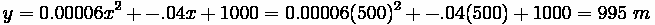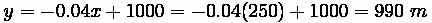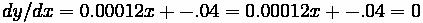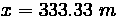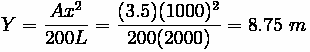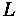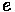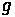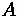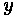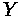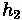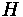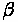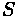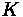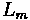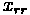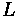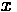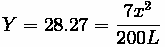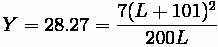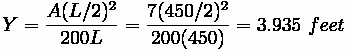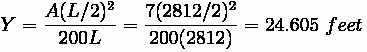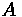


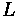

Fundamentals of Transportation/Vertical Curves
161
grades are generally described
as being in units of (m/m) or
(ft/ft), depending on unit type
chosen.
Both types of curves are in
parabolic form. Parabolic
functions have been found
suitable for this case because
they provide a constant rate of
A Typical Crest Vertical Curve (Profile View)
change of slope and imply
equal curve tangents, which
will be discussed shortly. The general form of the parabolic equation is defined below,
where
is the elevation for the parabola.
At x = 0, which refers to the position along the curve that corresponds to the PVC, the
elevation equals the elevation of the PVC. Thus, the value of equals
. Similarly, the
slope of the curve at x = 0 equals the incoming slope at the PVC, or
. Thus, the value of
equals
. When looking at the second derivative, which equals the rate of slope change,
a value for can be determined.
Thus, the parabolic formula for a vertical curve can be illustrated.
Where:
•
: elevation of the PVC
•
: Initial Roadway Grade (m/m)
•
: Final Roadway Grade (m/m)
•
: Length of Curve (m)
Most vertical curves are designed to be Equal Tangent Curves. For an Equal Tangent
Curve, the horizontal length between the PVC and PVI equals the horizontal length between the PVI and the PVT. These curves are generally easier to design.
Offset
Some additional properties of vertical curves exist. Offsets, which are vertical distances from the initial tangent to the curve, play a significant role in vertical curve design. The formula for determining offset is listed below.
Where:
•
: The absolute difference between
and
, multiplied by 100 to translate to a
percentage
•
: Curve Length
•
: Horizontal distance from PVC along curve
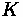

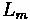
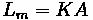
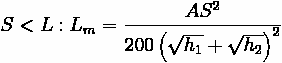
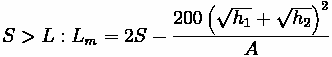
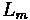
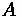
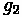
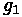

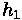
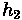
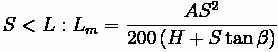
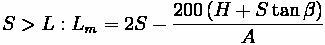
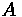
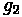
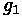
Fundamentals of Transportation/Vertical Curves
162
Stopping Sight Distance
Sight distance is dependent on the type of curve used and the design speed. For crest
curves, sight distance is limited by the curve itself, as the curve is the obstruction. For sag curves, sight distance is generally only limited by headlight range. AASHTO has several
tables for sag and crest curves that recommend rates of curvature,
, given a design
speed or stopping sight distance. These rates of curvature can then be mulitplied by the absolute slope change percentage,
to find the recommended curve length,
.
Without the aid of tables, curve length can still be calculated. Formulas have been derived to determine the minimum curve length for required sight distance for an equal tangent
curve, depending on whether the curve is a sag or a crest. Sight distance can be computed from formulas in other sections (See Sight Distance).
Crest Vertical Curves
The correct equation is dependent on the design speed. If the sight distance is found to be less than the curve length, the first formula below is used, whereas the second is used for sight distances that are greater than the curve length. Generally, this requires computation of both to see which is true if curve length cannot be estimated beforehand.
Where:
•
: Minimum Curve Length (m)
•
: The absolute difference between
and
, multiplied by 100 to translate to a
percentage
•
: Sight Distance (m)
•
: Height of driver's eye above roadway surface (m)
•
: Height of objective above roadway surface (m)
Sag Vertical Curves
Just like with crest curves, the correct equation is dependent on the design speed. If the sight distance is found to be less than the curve length, the first formula below is used, whereas the second is used for sight distances that are greater than the curve length.
Generally, this requires computation of both to see which is true if curve length cannot be estimated beforehand.
Where:
•
: The absolute difference between
and
, multiplied by 100 to translate to a
percentage
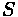
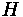
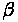
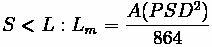
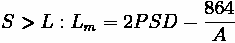
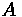

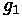

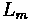


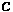
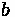

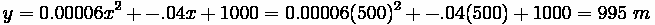
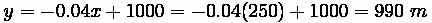
Fundamentals of Transportation/Vertical Curves
163
•
: Sight Distance (m)
•
: Height of headlight (m)
•
: Inclined angle of headlight beam, in degrees
Passing Sight Distance
In addition to stopping sight distance, there may be instances where passing may be
allowed on vertical curves. For sag curves, this is not an issue, as even at night, a vehicle in the opposing can be seen from quite a distance (with the aid of the vehicle's headlights).
For crest curves, however, it is still necessary to take into account. Like with the stopping sight distance, two formulas are available to answer the minimum length question,
depending on whether the passing sight distance is greater than or less than the curve
length. These formulas use units that are in metric.
Where:
•
: The absolute difference between
and
, multiplied by 100 to translate to a
percentage
•
: Passing Sight Distance (m)
•
: Minimum curve length (m)
Examples
Example 1: Basic Curve Information
Problem:
A 500-meter equal-tangent sag vertical curve has the PVC at station 100+00
with an elevation of 1000 m. The initial grade is -4% and the final grade is +2%.
Determine the stationing and elevation of the PVI, the PVT, and the lowest point
on the curve.
Solution:
The curve length is stated to be 500 meters. Therefore, the PVT is at station
105+00 (100+00 + 5+00) and the PVI is in the very middle at 102+50, since it
is an equal tangent curve. For the parabolic formulation, equals the elevation
at the PVC, which is stated as 1000 m. The value of equals the initial grade, which in decimal is -0.04. The value of can then be found as 0.00006.
Using the general parabolic formula, the elevation of the PVT can be found:
Since the PVI is the intersect of the two tangents, the slope of either tangent and the
elevation of the PVC or PVT, depending, can be used as reference. The elevation of the PVI can then be found:
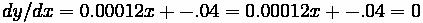
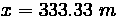


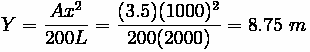

Fundamentals of Transportation/Vertical Curves
164
To find the lowest part of the curve, the first derivative of the parabolic formula can be found. The lowest point has a slope of zero, and thus the low point location can be found: Using the parabolic formula, the elevation can be computed for that location. It turns out to be at an elevation of 993.33 m, which is the lowest point along the curve.
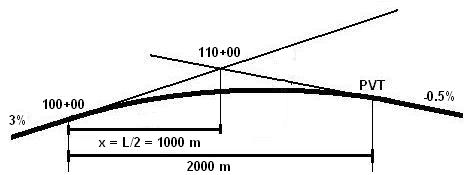
Example 2: Adjustment for Obstacles
Problem:
A current roadway is climbing a hill at an angle of +3.0%. The roadway starts at
station 100+00 and elevation of 1000 m. At station 110+00, there is an at-grade
railroad crossing that goes over the sloped road. Since designers are concerned
for the safety of drivers crossing the tracks, it has been proposed to cut a level tunnel through the hill to pass beneath the railroad tracks and come out on the opposite side. A vertical crest curve would connect the existing roadway to the proposed tunnel with a
grade of (-0.5)%. The prospective curve would start at station 100+00 and have a length of 2000 meters. Engineers have stated that there must be at least 10 meters of separation
between the railroad tracks and the road to build a safe tunnel. Assume an equal tangent curve. With the current design, is this criteria met?
Solution:
One way to solve this problem
would be to compute the
elevation of the curve at
station 110+00 and then see if
it is at least 10 meters from
the tangent. Another way
would be to use the Offset
Formula. Since A, L, and x are
all known, this problem can be
easily solved. Set x to 1000 meters to represent station 110+00.
The design DOES NOT meet the criteria.
Example 3: Stopping Sight Distance
Problem:
A current roadway has a design speed of 100 km/hr, a coefficient of friction of
0.1, and carries drivers with perception-reaction times of 2.5 seconds. The
drivers use cars that allows their eyes to be 1 meter above the road. Because of
ample roadkill in the area, the road has been designed for carcasses that are 0.5 meters in height. All curves along that road have been designed accordingly.



Fundamentals of Transportation/Vertical Curves
165
The local government, seeing the potential of tourism in the area and the boost to the local economy, wants to increase the speed limit to 110 km/hr to attract summer drivers.
Residents along the route claim that this is a horrible idea, as a particular curve called
"Dead Man's Hill" would earn its name because of sight distance problems. "Dead Man's Hill" is a crest curve that is roughly 600 meters in length. It starts with a grade of +1.0%
and ends with (-1.0)%. There has never been an accident on "Dead Man's Hill" as of yet, but residents truly believe one will come about in the near future.
A local politician who knows little to nothing about engineering (but thinks he does) states that the 600-meter length is a long distance and more than sufficient to handle the
transition of eager big-city drivers. Still, the residents push back, saying that 600 meters is not nearly the distance required for the speed. The politician begins a lengthy campaign to
"Bring Tourism to Town", saying that the residents are trying to stop "progress". As an engineer, determine if these residents are indeed making a valid point or if they are simply trying to stop progress?
Solution:
Using sight distance formulas from other sections, it is found that 100 km/hr has
an SSD of 465 meters and 110 km/hr has an SSD of 555 meters, given the
criteria stated above. Since both 465 meters and 555 meters are less than the
600-meter curve length, the correct formula to use would be:
Since the 1055-meter minimum curve length is greater than the current 600-meter length
on "Dead Man's Hill", this curve would not meet the sight distance requirements for 110
km/hr.
This seems like a very large gap. The question becomes, was the curve even good enough at 100 km/hr? Using the same formula, the result is:
740 meters for a minimum curve length is far greater than the existing 600-meter curve.
Therefore, the residents are correct in saying that "Dead Man's Hill" is a disaster waiting to happen. As a result, the politician, unable to hold public confidence by his "progress"
comment, was forced to resign.
Thought Question
Problem
Sag curves have sight distance requirements because of nighttime sight distance
constraints. The headlights on cars have a limited angle at which they can shine with bright enough intensity to see objects far off in the distance. If the government were to allow a wider angle of light to be cast out on standard car headlights, would this successfully
provide more stopping sight distance?
Solution
Yes, of course. For a single car traveling on a road with many sag curves, the design speed could be increased since more road could be seen. However, when additional cars were
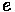
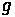
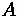
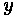
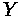

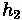
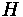
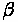
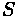
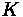
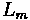
Fundamentals of Transportation/Vertical Curves
166
added to that same road, problems would begin to appear. With a greater angle of light
being cast from headlights, drivers in opposing lanes would be severely blinded, forcing them to slow down to avoid causing an accident. Just think of the last time somebody drove by with their 'brights' on and blinded you. This problem could cause more accidents and
force people to slow down, thus producing a net loss overall.
Sample Problem
Problem (Solution)
Variables
•
- Curve Length
•
- Elevation of designated point, such as PVC, PVT, etc.
•
- Grade
•
- Absolute difference of grade percentages for a certain curve, in percent
•
- Elevation of curve
•
- Offset between grade tangent from PVC and curve elevation for a specific station
•
- Height of driver's eye above roadway surface
•
- Height of object above roadway surface
•
- Height of headlight
•
- Inclined angle of headlight beam, in degrees
•
- Sight Distance in question
•
- Rate of curvature
•
- Minimum Curve Length
Key Terms
• PVC: Point of Vertical Curve
• PVI: Point of Vertical Intersection
• PVT: Point of Vertical Tangent
• Crest Curve: A curve with a negative grade change (like on a hill)
• Sag Curve: A curve with a positive grade change (like in a valley)



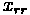


Fundamentals of Transportation/Vertical Curves/Problem
167
Fundamentals of Transportation/
Vertical Curves/Problem
Problem:
To help prevent future collisions between cars and trains, an at-grade crossing
of a rail road by a country road is being redesigned so that the county road will
pass underneath the tracks. Currently the vertical alignment of the county road
consists of an equal tangents crest vertical curve joining a 4% upgrade to a 3% downgrade.
The existing vertical curve is 450 feet long, the PVC of this curve is at station 48+24.00, and the elevation of the PVC is 1591.00 feet. The centerline of the train tracks is at station 51+50.00. Your job is to find the shortest vertical curve that provides 20 feet of clearance between the new county road and the train tracks, and to make a preliminary estimate of
the cut that will be needed to construct the new curve.
• Solution
Fundamentals of Transportation/
Vertical Curves/Solution
Problem:
To help prevent future collisions between cars and trains, an at-grade crossing
of a rail road by a country road is being redesigned so that the county road will
pass underneath the tracks. Currently the vertical alignment of the county road
consists of an equal tangents crest vertical curve joining a 4% upgrade to a 3% downgrade.
The existing vertical curve is 450 feet long, the PVC of this curve is at station 48+24.00, and the elevation of the PVC is 1591.00 feet. The centerline of the train tracks is at station 51+50.00. Your job is to find the shortest vertical curve that provides 20 feet of clearance between the new county road and the train tracks, and to make a preliminary estimate of
the cut at the PVI that will be needed to construct the new curve.
Solution:
A.) What is the curve length?
The curves are equal tangent, so we know that: PVI - PVC = PVT - PVI = L/2
From this, we know:
• PVC of First Curve: 48+24
• PVI of Both Curves (this is a constant): (48+24.00 + (450/2) = 50+49)
•
: Distance between PVI and railroad tracks: (51+50 - 50+49 = 101 feet)
• PVI Elevation: 1591 + (0.04*225) = 1600 feet
Use the offset formula for the first curve to find the vertical distance between the tangent and the curve:
Where:
•
= 7 (Change in Grade)
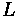
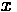
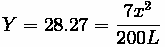

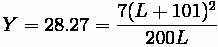
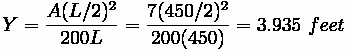
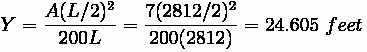
Fundamentals of Transportation/Vertical Curves/Solution
168
•
= 450 feet
•
= 51+50 - 48+24 = 326 feet
The offset, Y, at the railroad tracks's station is computed to be 8.27 feet.
The road is to be lowered an additional 20 feet. Therefore, the new offset at that sight would become 28.27 feet. The equation for the second curve becomes:
Neither L (length of curve) or x (distance of offset from PVC) are known. However, we know this is an equal tangent curve, meaning the distance from PVC to PVI is L/2 for the curve in question. Also, the distance between PVI and the railroad tracks is
, which is 101 feet.
Therefore, (L/2) +
equals the distance from PVC to the railroad tracks, which is what
we want for x. Thus, we are left with one unknown and one equation.
The new curve length is found to be 2812 feet.
B.) How deep is the cut at the PVI?
To find this, the offset formula can be used again, using the length L/2 as the distance from the PVC on any curve.
For the old curve, the offset is:
For the new curve, using data found from before, the offset is:
The difference between the two offsets is 20.67 feet. This is the depth of the cut at the PVI.
Transportation Economics/Pricing
169
Transportation Economics/Pricing
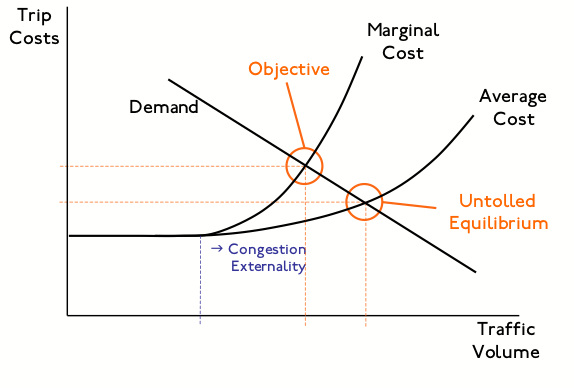
Pricing
Rationales for Pricing
• Revenue