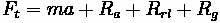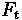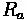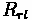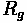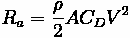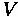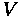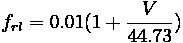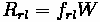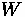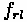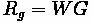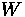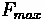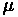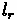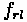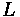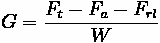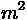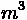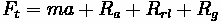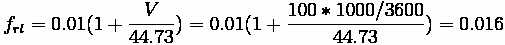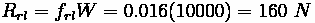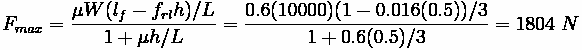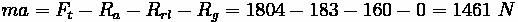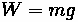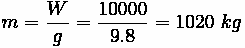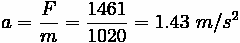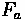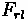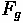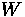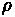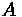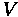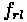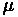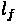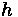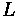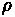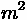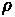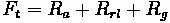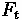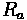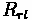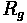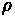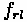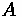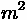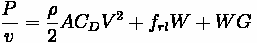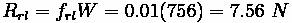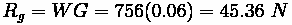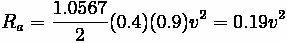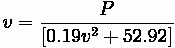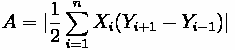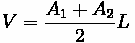139
Fundamentals of Transportation/
Sight Distance/Problem
Problem:
You see a body lying across the road and need to stop. If your vehicle was
initially traveling at 100 km/h and skids to a stop on a 2.5% upgrade, taking 75
m to do so, what was the coefficient of friction on this surface?
• Solution
Fundamentals of Transportation/
Sight Distance/Solution
Problem:
You see a a body lying across the road and need to stop. If your vehicle was
initially traveling at 100 km/h and skids to a stop on a 2.5% upgrade, taking 75
m to do so, what was the coefficient of friction on this surface?
Solution:
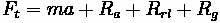
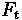


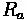
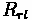
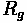
Fundamentals of Transportation/Grade
140
Fundamentals of Transportation/
Grade
Road Vehicle Performance forms the basics that make up highway design guidelines and traffic analysis. Roads need to designed so that the vehicles traveling upon them are
accommodated. For example, the Interstate Highway system in the United States has a
maximum allowable grade that can be used, so that the semitrucks that frequently use
these roads would be able to travel them without encountering grade problems. While this can pose quite a design challenge in mountainous regions like Colorado Rockies, without it those trucks would be forced to find better alternative routes, which costs time and money.
The ability of a certain vehicle type to use a road is dependent on the power produced by its motor, as well as other road-based and environmental characteristics. When choosing a
road design, these elements need to be considered.
Fundamental Characteristics
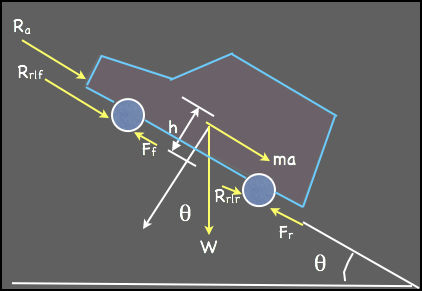
Tractive effort and resistance
are the two main forces that
oppose one another and
determine the performance of
roadway vehicles. Tractive
effort is the force exerted
against the roadway surface to
allow a vehicle to move
forward. Resistance
encompasses all forces that
push back and impede motion.
Both of these are in units of
force. The general formula for
this is outlined below:
Forces acting on a vehicle
Where:
•
= Tractive Effort
•
= Vehicle Mass
•
= Acceleration
•
= Aerodynamic Resistance
•
= Rolling Resistance
•
= Grade Resistance
These components are discussed in greater detail in the following sections.
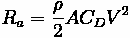
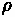
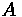

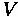
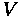
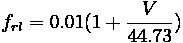
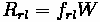
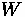
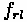
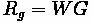
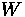

Fundamentals of Transportation/Grade
141
Aerodynamic Resistance
Aerodynamic resistance is a force that is produced by turbulent air flow around the vehicle body. This turbulence is dependent on the shape of the vehicle, as well as the friction of air passing over the vehicle's surface. A small portion of this resistance comes from air flow through vehicle components, such as interior ventilation. This resistance can be estimated through the following formula:
Where:
•
= Air Density
•
= Frontal area of the vehicle
•
= Coefficient of Drag
•
= Speed of the vehicle
Air density is a function of elevation and temperature. Frontal area and coefficient of drag are generally unique to each vehicle or type of vehicle.
Rolling Resistance
Rolling resistance is caused by a vehicle's internal mechanical friction and the interaction of tires with the roadway surface. Three main causes exist that create this resistance. The first is the rigidity of the tire and the roadway surface. The second is tire pressure and temperature. The third is vehicular operating speed. This value of rolling friction can be calculated from a very simplified formula, given here in metric.
is in meters per second.
The resistance caused by this friction will increase as weight is added to the vehicle.
Therefore, rolling resistance can be calculated.
Where:
•
= Vehicle Weight
•
= Rolling Friction
Grade Resistance
Grade resistance is the simplest form of resistance. It is the gravitational force acting on the vehicle. This force may not be exactly perpendicular to the roadway surface, especially in situations when a grade is present. Thus, grade resistance can be calculated in the
following formula:
Where:
•
= Vehicle Weight
•
= Grade (length/length)


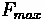
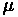

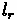

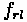

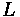
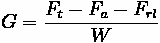

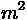
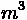
Fundamentals of Transportation/Grade
142
Tractive Effort
Tractive effort is the force that allows the vehicle to move forward, subject to the
resistances of the previous three forces. The derivation of the formula comes from
understanding the forces and moments that on around the various tires. It can be
summarized into a simple concept, illustrated here.
For a rear-wheel drive car:
For a front-wheel drive car:
Where:
•
= Maximum Tractive Effort
•
= Coefficient of road adhesion
•
= Vehicle Weight
•
= Distance from rear axle to vehicle's center of gravity
•
= Distance from front axle to vehicle's center of gravity
•
= Coefficient of rolling friction
•
= Height of the center of gravity above the roadway surface
•
= Length of wheelbase
Grade Computation
Most of the work surrounding tractive effort is geared toward determining the allowable
grade of a given roadway. With a certain known vehicle type using this road, the grade can be easily calculated. Using the force balance equation for tractive effort, a value for grade can be separating, producing the formula below:
This calculation produces the maximum grade allowed for a given vehicle type. It assumes that the vehicle is operating at optimal engine capacity and, thus, no acceleration can
occur, dropping that element from the overall equation.
Examples
Example 1: Racecar Acceleration
Problem:
A racecar is speeding down a level straightaway at 100 km/hr. The car has a
coefficient of drag of 0.3, a frontal area of 1.5
, a weight of 10 kN, a
wheelbase of 3 meters, and a center of gravity 0.5 meters above the roadway
surface, which is 1 meter behind the front axle. The air density is 1.054 kg/
and the
coefficient of road adhesion is 0.6. What is the rate of acceleration for the vehicle?


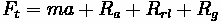


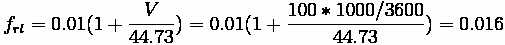
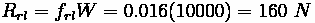
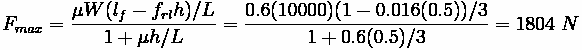
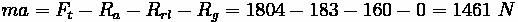
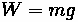
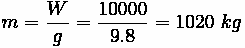
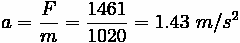



Fundamentals of Transportation/Grade
143
Solution:
Use the force balancing equation to solve for .
Since the straightaway is a level one, the grade is zero, thus removing grade resistance from the general problem.
Aerodynamic resistance is computed:
Rolling resistance is computed:
Tractive Effort is computed:
Looking back to the force balancing equation:
Divide out mass, which can be computed from weight by dividing out gravity.
Thus, divide mass from the force and acceleration can be found.
Thus, the vehicle is accelerating at a rate of 1.43 meters per second squared.
Example 2: Going Up a Hill
Problem:
Using the same case from Example 1, assume that instead the racecar
encounters a steep hill that it must travel up. It is desired that the driver
maintain the 100 km/hr velocity at a very minimum. With that being said, what
would be the maximum grade that the hill could be?
Solution:
At the steepest eligible hill, the racecar would be able to maintain 100 km/hr
without any room for acceleration or deceleration. Therefore, acceleration goes
to zero. All other values would stay the same from Example 1. Using the grade
formula, the maximum grade can be calculated.

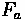
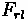
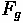
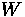


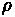
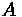

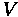
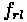

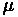

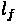
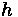
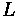
Fundamentals of Transportation/Grade
144
The maximum allowable grade is 14.61%.
Thought Question
Problem
Why is it that, in mountainous country, trucks and cars have different speed limits?
Answer
Tractive effort is one of the leading reasons, as trucks have a harder time going up steep hills than typical passenger cars, but it is not the only one. Safety is another leading reason, surprisingly, as big rig trucks are obviously more difficult to control in a harsh
environment, such as a mountain pass.
Sample Problem
Problem (Solution)
Variables
•
- Tractive Effort Force
•
- Aerodynamic resistance Force
•
- Rolling Resistance Force
•
- Grade Resistance Force
•
- Vehicle Weight
•
- Vehicle Mass
•
- Acceleration
•
- Air Density
•
- Frontal area of the vehicle
•
- Coefficient of Drag
•
- Speed of the vehicle
•
- Rolling Friction
•
- Grade
•
- Coefficient of road adhesion
•
- Distance from rear axle to vehicle's center of gravity
•
- Distance from front axle to vehicle's center of gravity
•
- Height of the center of gravity above the roadway surface
•
- Length of wheelbase

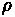
Fundamentals of Transportation/Grade
145
Key Terms
• Tractive Effort
• Aerodynamic Resistance
• Rolling Resistance
• Grade Resistance
Fundamentals of Transportation/
Grade/Problem
Problem:
It has been estimated that a Tour-de-France champion could generate a
sustained 510 Watts of power while a healthy young human male (HYHM) can
generate about 310 Watts of power. The bicycling champion and HYHM are
going to race (on bicycles) up a hill with a 6% upgrade, that is five miles long, and the elevation at the top of the hill is 5000 feet. Both rider/bicycle combinations weigh 170 lbs, with frontal area 0.4m2 and coefficient of drag 0.9 (values being typical of bicyclists in crouched racing positions). The coefficient of rolling resistance for both bicycles is 0.01.
Assume is 1.0567 kg/cubic-m. Remember, power equals the product of force and velocity.
(1) Who gets to the top first? (2) How much longer does it take the loser to make it to the top?
• Solution


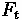


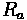
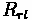
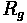
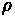

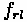

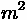


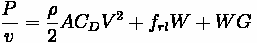
Fundamentals of Transportation/Grade/Solution
146
Fundamentals of Transportation/
Grade/Solution
Problem:
It has been estimated that a Tour-de-France champion could generate a
sustained 510 Watts of power while a healthy young human male (HYHM) can
generate about 310 Watts of power. The bicycling champion and HYHM are
going to race (on bicycles) up a hill with a 6% upgrade, that is five miles long, and the elevation at the top of the hill is 5000 feet. Both rider/bicycle combinations weigh 170 lbs, with frontal area 0.4
and coefficient of drag 0.9 (values being typical of bicyclists in
crouched racing positions). The coefficient of rolling resistance for both bicycles is 0.01.
Assume is 1.0567 kg/cubic-m. Remember, power equals the product of force and velocity.
(1) Who gets to the top first? (2) How much longer does it take the loser to make it to the top?
Solution:
The winner is obvious the Tour-de-France champion, as everything between the
two is equal with the exception of power. Since the champion produces more
power, he, by default, would win.
We need to find the maximum steady state speed for each racer to compute the differences in arrival time. At the steady state speed we must have:
Where:
•
= Tractive Effort
•
= Vehicle Mass
•
= Acceleration
•
= Aerodynamic Resistance
•
= Rolling Resistance
•
= Grade Resistance
We also know:
•
= 1.0567 kg/cubic-m
•
= 756 N
•
= 0.01
•
= 0.06
•
= 0.4
•
= 0.9
To estimate available tractive effort we can use the definition of power as time rate of work, P = FV, to get:
Substituting in the components of the individual formulas to the general one, we get:
If we compute rolling and grade resistance, we get:
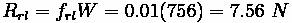
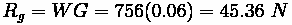
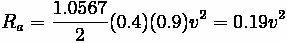
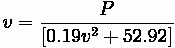

Fundamentals of Transportation/Grade/Solution
147
Together, they add up to 52.92 N.
Aerodynamic Resistance can be found to be:
With everything substituted into the general formula, the end result is the following
formulation:
This problem can be solved iteratively (setting a default value for v and then computing through iterations) or graphically. Either way, when plugging in 510 watts for the
Tour-de-France champion, the resulting velocity is 7.88 meters/second. Similarly, when
plugging in 310 watts for the HYHM, the resulting velocity is 5.32 meters/second.
The hill is five miles in length, which translates to 8.123 kilometers, 8,123 meters. It will take the champion 1030 seconds (or 17.1 minutes) to complete this link, whereas the
HYHM will take 1527 seconds (or 25.4 minutes). The resulting difference is 8.3 minutes.
Fundamentals of Transportation/
Earthwork
Earthwork is something that
transportation projects seldom
avoid. In order to establish a
properly functional road, the
terrain must often be adjusted.
In many situations, geometric
design will often involve
minimizing the cost of
earthwork movement.
Earthwork is expressed in
units of volumes (cubic meters
The equipment necessary for earthwork to occur
in metric). Increases in such
volumes require additional trucks (or more runs of the same truck), which cost money.
Thus, it is important for designers to engineer roads that require very little earthwork.
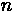
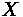
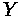
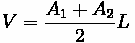
![]()