([1−δ ij( z)) Mijz]}
(8)
i=1 j=1
Eq. 8 shows the system has been split into linear and nonlinear part, Fig. 4. Notice that the
first column of Mij depends on i while the second column depends on j Hence, the resulting
nonlinear part ϕ(z) such that:
m n
ϕ( z) = ∑ ∑(1−δ ij ( z)) Mij z
(9)
i=1 j=1
is additively decomposable (Cuesta, Gordillo et al. 1999), that is:
ϕ(z) = ϕ(z1, z2) = ϕ(z1, 0) + ϕ(0, z2)
(10)
(see (Cuesta, Gordillo et al. 1999) for the proof)
220
New Approaches in Automation and Robotics
Eq. 10 implies that the nonlinear part ϕ is additively decomposable, and therefore
techniques used for stability analysis of SISO system can be used to stabilize the multi-input
multi-output systems. This can be done by adding a number of small fuzzy systems equal to
the number of the output variables in the feedback loop of the MIMO system for each input
variable as shown in Fig. 12. In this way all the nonlinearities of the fuzzy system can be
included within a bounded sector.
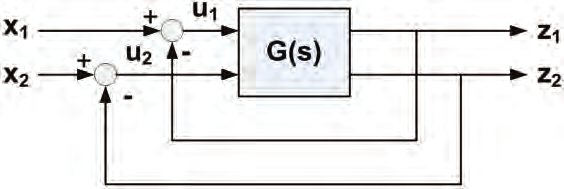
Fig. 12 The proposed MIMO fuzzy feedback system
6.2 Stability analysis of closed loop MIMO system
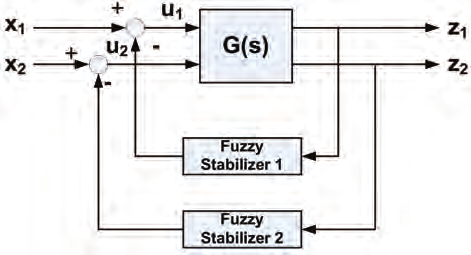
A simple stability analysis for closed loop system is shown in Fig. 13 (a). In this system the
proposed fuzzy stabiliser is placed on each feedback loop for each input as shown in Fig.
13(b). That includes all the nonlinearities of the system.
Fig. 13.(a) MIMO closed loop system
Fuzzy Stabilization of Fuzzy Control Systems
221
Fig. 13.(b) MIMO closed loop system with fuzzy stabilizers
6.3 Simulation example
Consider a MIMO system with a state space representation:
⎡ 1
x& ⎤ ⎡−7 −7 −50⎤ ⎡ 1
x ⎤ ⎡1 0⎤
⎢ ⎥ ⎢
⎥ ⎢ ⎥ ⎢
⎥ ⎡ 1
u ⎤
x&
= 1
0
0
x
+
⎢ 2 ⎥ ⎢
⎥ ⎢ 2 ⎥ ⎢0 1⎥ ⎢ ⎥
⎣ u 2 ⎦
⎢ x& ⎥ ⎢ 0
1
0 ⎥ ⎢ x ⎥ ⎢0 0⎥
⎣ 3 ⎦ ⎣
⎦ ⎣ 3 ⎦ ⎣
⎦
⎡ 1
x ⎤
⎡ 1
y ⎤ ⎡−1 0 0⎤ ⎢ ⎥
=
⎢ ⎥ ⎢
⎥ ⎢ x 2 ⎥
⎣ y 2 ⎦ ⎣ 0 1 0⎦ ⎢ x ⎥
⎣ 3 ⎦
In our problem we will find a transfer function of the model of the form:
⎡ 1
y ⎤ ⎡ 11
G
12
G ⎤ ⎡ 1
u ⎤
=
⎢ ⎥ ⎢
⎥ ⎢ ⎥
⎣ y 2 ⎦ ⎣ G 21 G 22 ⎦ ⎣ u 2 ⎦
2
s
where
11
G =
3
s + 7 2
s + 7 s + 50
− s
G 21 =
3
s + 7 2
s + 7 s + 50
7 s + 50
12
G =
3
s + 7 2
s + 7 s + 50
2
s + 7 s
G 22 =
3
s + 7 2
s + 7 s + 50
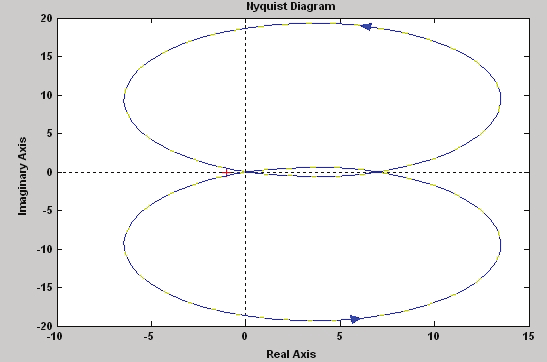
Using the analysis described in section 5 and by aid of Nyquist plot of the system as shown
1
in Fig. 14 we can determine −
= 6
− 45
.
, as a result M/L ≤ 0.155.
β
Note that, for all the components of the system (G11, G12, G21, and G22), the denominator
in each case remains the same, since it holds the key to the system stability.
222
New Approaches in Automation and Robotics
Fig. 14 The Nyquist plot of the simulated system
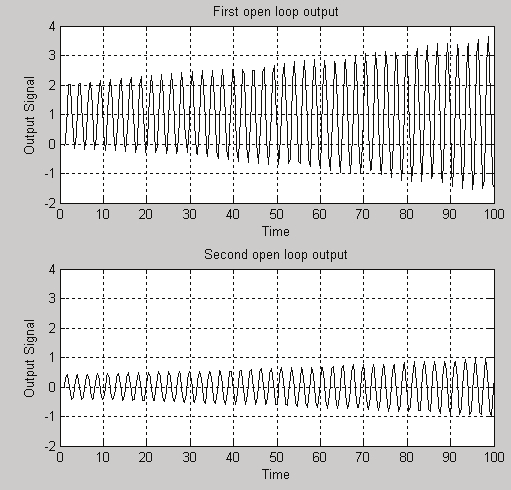
The outputs of the open loop system show the system instability as shown in Fig. 15.
Fig. 15 The open loop response of the simulated system
Fuzzy Stabilization of Fuzzy Control Systems
223
When the fuzzy stabilizers are added to the system according to Fig. 12 and the fuzzy
parameters are set such that the ratio M/L ≤ 0.007 is kept the same as follow:
Stabilizer (1)
M11= 3.1
, L11= 25
Stabilizer (2)
M12= 1.8
, L12= 12
Stabilizer (3)
M21= 0.031
, L21= 0.25
Stabilizer (4)
M22= 0.018
, L22= 0.12
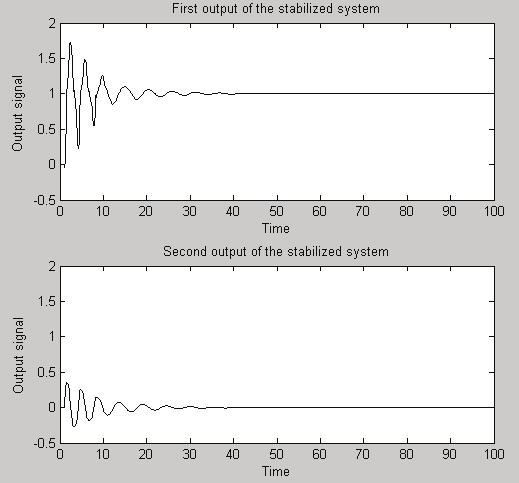
The simulation results in Fig. 16 show the output of the stabilized system.
Fig. 16 The outputs of the stabilized simulated system
The proposed technique has the advantage of keeping the system stable even if the system
nonlinearities have been changed provided that they still remain within the bounded sector
proposed.
7. Conclusion
This chapter presented a practical approach to stabilize fuzzy systems based on adaptive
nonlinear feedback using a fuzzy stabilizer in the feedback loop. For this we needed to
identify the nonlinearity range of the system. The fuzzy stabilizer is tuned so that the system
nonlinearities lie in a bounded sector as delivered by using the circle criterion theory.
Because of circle criterion’s graphical nature; the designer is given a physical feel for the
system. The concept has been used to ensure stability of a car-like robot controller. In
addition, the idea has been extended to stabilize MIMO systems based on the additively
decomposition technique.
224
New Approaches in Automation and Robotics
The advantage of the proposed approach is the simplicity of the design procedure especially
for the MIMO systems analysis and implementation. The use of the fuzzy system to control
the feedback loop using its approximate reasoning algorithm gives a good opportunity to
handle the practical system uncertainty. The approach described have provided a quick and
easy stabilization process which can allow designers to fine tune their controllers
performance without at the same time, worrying about stability issues It is also shown that
the fuzzy stabilizer can be integrated, with small modifications, in any fuzzy controller to
enhance its stability. As a result it is suitable for hardware implementation or even to
modify existence software and hardware design if required to ensure system stability.
8. References
Abdelnour, G., J. Y. Cheung, et al. (1993). "Application of Describing Functions in the
Transient Respose Analysis of Three Term Fuzzy Controller." IEEE Transaction on
System, Man and Cybernetics 23: 603-606.
Aracil, J. and F. Gordillo (2004). "Describing function method for stability analysis of PD and
PI fuzzy controllers." Fuzzy Sets and Systems 143: 233-249.
Babuska, R., J. Roubos, et al. (1998). Identification of MIMO systems by input-output TS
fuzzy models. In the proceedings of The 1998 IEEE International Conference on
Fuzzy systems, IEEE World Congress on Computational Intelligence.
Buckley, J. J. and E. Eslami (2002). An Introduction to Fuzzy Logic and Fuzzy Sets, Phydica-
Verlag Heidelberg.
Cuesta, F., F. Gordillo, et al. (1999). "Stability Analysis of Nonlinear Multivariable Takagi–
Sugeno Fuzzy Control Systems." IEEE Transaction on Fuzzy Systems 7(5): 508-520.
Cuesta, F. and A. Ollero (2004). "Fuzzy control of reactive navigation with stability analysis
based on conicity and Lyapunov theory." Journal of Control Engineering Practice
12: 625-638.
Espada, A. and A. Barreiro (1999). "Robust stability of fuzzy control systems based on
conicity conditions." Automatica 35: 643-654.
Farinwata, S. S., D. Filev, et al. (2000). Fuzzy Control: Synthesis and Analysis, John Wiley &
Sons Ltd.
Fuh, C.-C. and P.-C. Tung (1997). "Robust stability analysis of fuzzy control systems." Fuzzy
Sets and Systems 88: 289-298.
Gang, J. and C. Laijiu (1996). "Linguistic stability analysis of fuzzy closed loop control
systems." Fuzzy Sets and Systems 82: 27-34.
Giron-Sierra, J. M. and G. Ortega (2002). A Survey of Stability of Fuzzy Logic Control with
Aerospace Applications. 15th Triennial World Congress. Barcelona, Spain.
Gruyitch, L., J.-P. Richard, et al. (2004). Stability Domains, Chapman& Hall/CRC.
J. Yen, R. L., and L. A. Zadeh (1995). Industrial applications of fuzzy logic and intelligent
systems, IEEE Press.
Jenkins, D. and K. M. Passino (1999). "An Introduction to Nonlinear Analysis of Fuzzy
Control Systems." Journal of Intelligent and Fuzzy Systems, 17(1): 75–103.
Kandel, A., Y. LUO, et al. (1999). "Stability analysis of fuzzy control systems." Fuzzy Sets
and Systems 105: 33-48.
Fuzzy Stabilization of Fuzzy Control Systems
225
Kang, H.-J., C. Kwon, et al. (1998). "Robust Stability Analysis and Design Method for the
Fuzzy Feedback Linearization Regulator." IEEE Transaction on Fuzzy Systems 6(4):
464-472.
Katoh, R., T. Yamashita, et al. (1995). "Stability analysis of control system having PD type of
fuzzy controller." Fuzzy Sets and Systems 74: 321-334.
Lam, H. K. and L. D. Seneviratne (2007). "LMI-based stability design of fuzzy controller for
nonlinear systems." IET Control Theory Appl. 1(1): 393-401.
Lin, C., Q.-G. Wang, et al. (2007). "Stability conditions for time-delay fuzzy systems using
fuzzy weighting-dependent approach." IET Control Theory Appl. 1(1): 127-132.
Mannani, A. and H. A. Talebi (2007). "A Fuzzy Lyapunov-Based Control Strategy for a
Macro–Micro Manipulator: Experimental Results." IEEE Transactions on Control
Systems Technology 15(2): 375-383.
Piegat, A. (1997). Hyperstability of fuzzy-control systems and degrees of freedom. In the
proceedings of EUFIT’97.
Ray, K. S., A. M. Ghosh, et al. (1984). "L2-Stability and the related design concept for SISO
linear systems associated with fuzzy logic controllers." IEEE Transactions on
Systems, Man, and Cybernetics SMC-14(6): 932–939.
Ray, K. S. and D. D. Majumderr (1984). "Application of circle criteria for stability analysis of
linear SISO and MIMO systems associated with fuzzy logic controllers." IEEE
Transactions on Systems, Man, and Cybernetics SMC-14(2): 345–349.
Reznik, L. (1997). Fuzzy Contollers, Newnes.
Rubio, J. d. J. and W. Yu (2007). "Stability Analysis of Nonlinear System Identification via
Delayed Neural Networks." IEEE TRANSACTIONS ON CIRCUITS AND
SYSTEMS-II: EXPRESS BRIEFS 54(2): 161-165.
Safonov, M. G. (1980). Stability and Roboustness of Multivariable Feedback Systems. Unites
State of America, The Massachusetts Institute Of Technology.
Safonov, M. G. (1980). Stability and Robustness of Multivariable Feedback systems, The
Massachusetts Institute of Technology.
Tanaka, K. and M. Sugeno (1992). "Stability analysis and design of fuzzy control systems."
Fuzzy Sets and Systems 45: 135-156.
Thathachar, M. A. L. and P. Viswanath (1997). "On the stability of fuzzy systems." IEEE
Transaction on Fuzzy Systems 5(1): 145-151.
Vidyasagar, M. (1993). Nonlinear Systems Analysis. Englewood, Cliffs, New Jersey, Prentice
Hall, Inc.
Wang, H. O., K. Tanaka, et al. (1996). "An Aproach to Fuzzy Control of Nonlinear Systems:
Stability and Design Issues." IEEE Trans. Fuzzy Systems 4: 14-23.
Wang, W. J. and H. R. Lin (1998). "Fuzzy control design for the trajectory tracking in phase
plane." IEEE Transaction on System, Man and Cybernetics, part A 28(5): 710-719.
Wu, S. J. and T. L. Ch. (2000). "Optimal fuzzy controller design: Local concept approach."
IEEE Trans. Fuzzy Systems 8(2): 171-185.
Ying, H. (1996). "Structure Decomposition of the General MIMO Fuzzy Systems."
International Journal of Intelligent Control and Systems 1(3): 327-337.
226
New Approaches in Automation and Robotics
Ying, H. (1999). "Analytical analysis and feedback linearization tracking control of the
general Takagi-Sugeno fuzzy dynamic systems." IEEE Transaction on system, Man
and Cybernetics, part C 29(2): 290-298.
Zuo, Z. and Y. Wang (2007). "Robust stability and stabilisation for nonlinear uncertain time-
delay systems via fuzzy control approach." IET Control Theory Appl. 1(1): 422-429.
13
Switching Control in the Presence of
Constraints and Unmodeled Dynamics
Vojislav Filipovic
Regional center for talents, Loznica
Serbia
1. Introduction
Recently there has been increased research interest in the study of the hybrid dynamical
systems (Sun & Ge, 2005) and (Li et al., 2005). These systems involve the interaction of
discrete and continuous dynamics. Continuous variables take the values from the set of real
numbers and the discrete variables take the values from finite set of symbols. The hybrid
systems have the behaviour of an analog dynamic system before certain abrupt structural or
operating conditions are changed. The event driven dynamics in hybrid control systems can
be described using different frameworks from discrete event systems (Cassandras &
Lafortune, 2008) such as timed automata, max-plus algebra or Petry nets. For dynamic
systems whose component are dominantly discrete event, main tools for analysis and design
are representation theory, supervisory control, computer simulation and verification. From
the clasical control theory point of view, hybrid systems may be considered as a switching
control between analog feedback loops. Generally, hybrid systems can achieve better
performance then non-switching controllers because they can to reconfigure and reorganize
their structures. For that is necessery correct coordination of discrete and analog control
variables.
The mathematical model for real process, generally, has the Hammerstein-Wiener form
(Crama & Atkins, 2001) and (Zhao & Chen, 2006). It means that on the input and output of
the process are present nonlinear elements (actuator and sensor). Here we will consider
Hammerstein model which has the input saturation as nonlinear element. That is the most
frequent nonlinearity encountered in practice (Hippe, 2006). Also, unmodeled dynamics
with matching condition is present. As a control strategy will be used switching control. The
switched systems can be viewed as higher abstraction of hybrid systems.
The design of switching controllers having guaranted stability, known as the picewise linear
LQ control (PLC), is first considered in (Wredenhagen & Belanger, 1994). The picewise
linear systems are systems that have different linear dynamics in different regions of the
continuous state space (Johansson, 2003). The PLC control has the associated switching
surfaces in form of positively invariant sets and yields a relatively low-gain controller. In the
LHG (low-and-high gain) design a low gain feedback law is first designed in such a way
228
New Approaches in Automation and Robotics
that the actuator does not saturate in magnitude and the closed – loop system remains
linear. The low gain enlarge the region in which the closed-loop system remains linear and
enlarge the basin of attraction of the closed-loop systems (Lin, 1999). After that, using
appropriate Lyapunov function for the closed-loop system, under this low gain feedback
control law, a linear high gain feedback law is designed and added to the low gain feedback
control. Combination of LHG and PLC gives the robust controllers with fast transience. The
key feature of PLC/LHG controllers is that the saturation level is avoided. But, it has been
recognized in references (Lin et al., 1997) and (De Dona et al., 2002) that the performance of
closed-loop system can be further improved by forcing the control into saturation. Such
controller increases the value of the switching regions so that each linear controller is able to
act in a region where a degree of over-saturation is reached. The over-saturation means that
the controller demands for input level is greater than the avaliable range.
The actuator rate saturation, also, is important problem. Namely, the phase lag associated
with saturation rate has a destabilizing effect (Saberi et al., 2000). The problem is more
severe when the actuator is, also, subject to magnitude saturation since small actuator
output results in small stability margin even in the absence of rate saturation (Lin et al.,
1997).
The problem is more complex in the presence of delay in the system. The paper
(Tarbouriech & da Silva, 2000) deals with the synthesis of stabilizing controllers for linear
systems with state delay and saturation controls. Performance guided hybrid LQ controller
for discrete time-delay systems is considered in (Filipovic, 2005). In (Wu et al., 2007) the
method for designing an output feedback law that stabilize a linear system subject to
actuator saturation with large domain of attraction is considered. It is usually true that
higher performance levels are associated with pushing the limits (Goodwin et al., 2005).
That is motivation to operate the system on constraint bounderies. It means that problem
with actuator saturation can be considered as optimisation with constraints.
In this paper the robustness of picewise linear LQ control with prescribed degree of stability
using switching, low-and-high gain and over-saturation is considered. The process is
described with linear uncertain dynamic system in the state space form. Structure of the
uncertaintes is defined with matching conditions. By the Lyapunov stability criterion
(Michel et al., 2008) it is shown that a robust PLC/LHG controller with allowed over-
saturation, can exponentially stabilize linear uncertain systems with prescribed exponential
rate. This approach is different in comparison with (De Dona et al., 2002) where the Riccati
equation approach is used.
2. Switching controller with prescribed degree of stability
The dynamic system subject to input saturation can be described in the next form
x&(t) = Ax(t) + BsatΔu(t) , x(t =
∈ ⊂
0 )
n
x0 X R
(1)
Where
n
x ∈ R and
m
u ∈ R . Nonlinear input function (saturation function) is defined as
m
m
sat : R →
Δ
R
Switching Control in the Presence of Constraints and Unmodeled Dynamics
229
Δ = [Δ
Δ
Δ >
=
1 ,L, m ]
, i
0 i
,
1,2,L,m
satΔ ( u) = [ satΔ ( u 1),L, satΔ ( u )] T
m
1
m
Δ
satΔ (u =
Δ (2)
i
i ) sign (
ui )min
( ui , i)
The ui is the ith element of vector u. As in (Wredenhagen & Belanger, 1994) we take a
sequence {ρ
ρ > ρ L > ρ >
i }N such that
1
2
N
0 and matrix Q > 0 . Then that one can to
i=1
define matrix
R =
>
=
i
diag[r1i , r2i ,L, rm
i ]
r
,
j
0
, j 1,2,L, m
i
(3)
Design of optimal LQ regulator with prescribed degree of stability is based on minimization
of next functional
∞
J(x , α
0
)= ∫ 2αt
e
[ Tx(t) (
Qx t)+ T
v (t)R v(t)
i
]dt
(4)
t0
The quantity α in (4) defines the degree of system stability for the feedback control systems.
From (4) for every Ri we can get matrices Pi and Ki from equations
(A + αI)TP +
+ α −
−
+
=
i
P (
i A
I) PiBR 1
i BTPi
Q 0
(5)
1 T
K
−
=
i
Ri B i
P
(6)
where Pi is the positive solution of the algebraic Riccati equation (5) for the optimal LQ
problem. Matrix K i is gain of the controller.
The switching surfaces are ellipsoids defined by
Δ
E =









