cn to make Equation true. If f[ n] is finite energy ( f[ n]∈ L 2[0, N] ), then the equality in Equation
holds in the sense of energy convergence; with discrete-time signals, there are no concerns for
divergence as there are with continuous-time signals.
The cn - called the Fourier coefficients - tell us "how much" of the sinusoid ⅇjω 0 kn is in f[ n] . The formula shows f[ n] as a sum of complex exponentials, each of which is easily processed by an LTI
system (since it is an eigenfunction of every LTI system). Mathematically, it tells us that the set
of complex exponentials { ⅇjω 0 kn , k∈ℤ } form a basis for the space of N-periodic discrete time
functions.








Equations
Now, in order to take this useful tool and apply it to arbitrary non-periodic signals, we will have to
delve deeper into the use of the superposition principle. Let sT( t) be a periodic signal having
period T. We want to consider what happens to this signal's spectrum as the period goes to
infinity. We denote the spectrum for any assumed value of the period by cn( T). We calculate the
spectrum according to the Fourier formula for a periodic signal, known as the Fourier Series (for
more on this derivation, see the section on Fourier Series.)
()
where
and where we have used a symmetric placement of the integration interval about the
origin for subsequent derivational convenience. We vary the frequency index n proportionally as
we increase the period. Define
()
making the corresponding Fourier Series
()
As the period increases, the spectral lines become closer together, becoming a continuum.
Therefore,
()
with
()
(3.16)
Discrete-Time Fourier Transform
(3.17)
Inverse DTFT
Warning
It is not uncommon to see the above formula written slightly different. One of the most
common differences is the way that the exponential is written. The above equations use the


radial frequency variable ω in the exponential, where ω=2 πf , but it is also common to include
the more explicit expression, ⅈ2πft , in the exponential. Sometimes DTFT notation is
expressed as F( ⅇⅈω) , to make it clear that it is not a CTFT (which is denoted as F( Ω) ). Click
here for an overview of the notation used in Connexion's DSP modules.
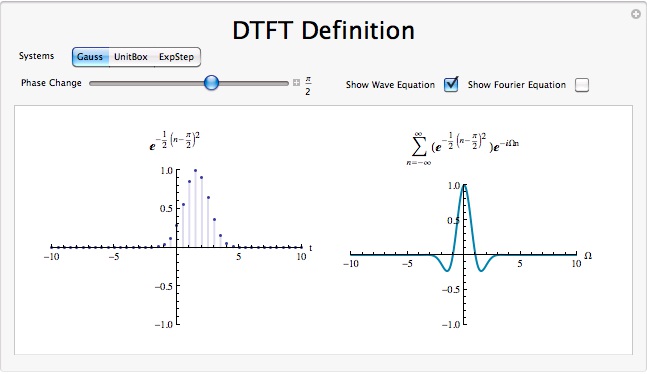
DTFT Definition demonstration
Figure 3.9.
Click on the above thumbnail image (when online) to download an interactive Mathematica Player demonstrating Discrete Time
Fourier Transform. To Download, right-click and save target as .cdf.
DTFT Summary
Because complex exponentials are eigenfunctions of LTI systems, it is often useful to represent
signals using a set of complex exponentials as a basis. The discrete time Fourier transform
synthesis formula expresses a discrete time, aperiodic function as the infinite sum of continuous
frequency complex exponentials.
()
The discrete time Fourier transform analysis formula takes the same discrete time domain signal
and represents the signal in the continuous frequency domain.
()
3.5. Continuous-Time Fourier Transform*




3.5. Continuous-Time Fourier Transform*
In this lab, we learn how to compute the continuous-time Fourier transform (CTFT), normally
referred to as Fourier transform, numerically and examine its properties. Also, we explore noise
cancellation and amplitude modulation as applications of Fourier transform.
Properties of CTFT
The continuous-time Fourier transform (CTFT) (commonly known as Fourier transform) of an
aperiodic signal x( t) is given by
(3.18)
The signal x( t) can be recovered from X( ω) via this inverse transform equation
(3.19)
Some of the properties of CTFT are listed in Table 3.1.
Table 3.1. Properties of CTFT
Properties
Time domain
Frequency domain
Time shift
x ( t − t 0 )
X ( ω ) e − jωt 0
Time scaling
Linearity
a 1 x 1 ( t ) + a 2 x 2 ( t ) a 1 X 1 ( ω ) + a 2 X 2 ( ω ) Time convolution
x ( t ) ∗ h ( t )
X ( ω ) H ( ω )
Frequency convolution x ( t ) h ( t )
X ( ω ) ∗ H ( ω )
Refer to signals and systems textbooks m31521 - m31521 for more theoretical details on this transform.
Numerical Approximations to CTFT
Assuming that the signal x( t) is zero for t<0 and t≥ T, we can approximate the CTFT integration in Equation (1) as follows:




(3.20)
where T= Nτ and N is an integer. For sufficiently small τ, the above summation provides a close
approximation to the CTFT integral. The summation
is widely used in digital signal
processing (DSP), and both LabVIEW MathScript and LabVIEW have a built-in function for it
called fft. In a .m file, if N samples x( nτ) are stored in a vector x, then the function call
>>xw=tau*fft (x)
calculates
(3.21)
where
(3.22)
with N assumed to be even. The fft function returns the positive frequency samples before the
negative frequency samples. To place the frequency samples in the right order, use the function
fftshift as indicated below:
>>xw=fftshift(tau*fft (x ) )
Note that X( ω) is a vector (actually, a complex vector) of dimension N. X( ω) is complex in
general despite the fact that x( t) is real-valued. The magnitude of X( ω) can be computed using the
function abs and the phase of X( ω) using the function angle.
3.6. Introduction*
Contents of Sampling chapter
Introduction(Current module)
Proof
Illustrations

Matlab Example
Hold operation
System view
Aliasing applet
Exercises
Table of formulas
Why sample?
This section introduces sampling. Sampling is the necessary fundament for all digital signal
processing and communication. Sampling can be defined as the process of measuring an analog
signal at distinct points.
Digital representation of analog signals offers advantages in terms of
robustness towards noise, meaning we can send more bits/s
use of flexible processing equipment, in particular the computer
more reliable processing equipment
easier to adapt complex algorithms
Claude E. Shannon
Figure 3.10.
Claude Elwood Shannon (1916-2001)
Claude Shannon has been called the father of information theory, mainly due to his landmark papers on the "Mathematical theory of communication" . Harry Nyquist was the first to state

the sampling theorem in 1928, but it was not proven until Shannon proved it 21 years later in the
paper "Communications in the presence of noise" .
Notation
In this chapter we will be using the following notation
Original analog signal x( t)
Sampling frequency Fs
Sampling interval Ts (Note that:
)
Sampled signal xs( n) . (Note that xs( n)= x( nTs) )
Real angular frequency Ω
Digital angular frequency ω. (Note that: ω= ΩTs )
The Sampling Theorem
The Sampling theorem
When sampling an analog signal the sampling frequency must be greater than twice the
highest frequency component of the analog signal to be able to reconstruct the original signal
from the sampled version.
Finished? Have at look at: Proof; Illustrations; Matlab Example; Aliasing applet; Hold
operation; System view; Exercises
3.7. Proof*
Sampling theorem
In order to recover the signal x( t) from it's samples exactly, it is necessary to sample x( t) at a



rate greater than twice it's highest frequency component.
Introduction
As mentioned earlier, sampling is the necessary fundament when we want to apply digital signal
processing on analog signals.
Here we present the proof of the sampling theorem. The proof is divided in two. First we find an
expression for the spectrum of the signal resulting from sampling the original signal x( t). Next we
show that the signal x( t) can be recovered from the samples. Often it is easier using the frequency
domain when carrying out a proof, and this is also the case here.
Key points in the proof
We find an equation for the spectrum of the sampled signal
We find a simple method to reconstruct the original signal
The sampled signal has a periodic spectrum...
...and the period is 2π Fs
Proof part 1 - Spectral considerations
By sampling x( t) every Ts second we obtain xs( n). The inverse fourier transform of this time
discrete signal is
()
For convenience we express the equation in terms of the real angular frequency Ω using ω= ΩTs .
We then obtain
()
The inverse fourier transform of a continuous signal is
()
From this equation we find an expression for x ( nTs)









()
To account for the difference in region of integration we split the integration in Equation into
subintervals of length
and then take the sum over the resulting integrals to obtain the complete
area.
()
Then we change the integration variable, setting
()
We obtain the final form by observing that ⅇⅈ 2π kn= 1 , reinserting η= Ω and multiplying by
()
To make xs( n)= x( nTs) for all values of n, the integrands in Equation and Equation have to agreee, that is
()
This is a central result. We see that the digital spectrum consists of a sum of shifted versions of
the original, analog spectrum. Observe the periodicity!
We can also express this relation in terms of the digital angular frequency ω= ΩTs
()
This concludes the first part of the proof. Now we want to find a reconstruction formula, so that
we can recover x( t) from xs( n).
Proof part II - Signal reconstruction
For a bandlimited signal the inverse fourier transform is








()
In the interval we are integrating we have:
. Substituting this relation into Equation
we get
()
Using the DTFT relation for Xs( ⅇⅈΩTs) we have
()
Interchanging integration and summation (under the assumption of convergence) leads to
()
Finally we perform the integration and arrive at the important reconstruction formula
()
(Thanks to R.Loos for pointing out an error in the proof.)
Summary
Spectrum sampled signal
Reconstruction formula
Go to Introduction; Illustrations; Matlab Example; Hold operation; Aliasing applet; System
view; Exercises ?
3.8. Illustrations*
In this module we illustrate the processes involved in sampling and reconstruction. To see how all
these processes work together as a whole, take a look at the system view. In Sampling and
reconstruction with Matlab we provide a Matlab script for download. The matlab script shows
the process of sampling and reconstruction live.
Basic examples
Example 3.6.
To sample an analog signal with 3000 Hz as the highest frequency component requires
sampling at 6000 Hz or above.
Example 3.7.
The sampling theorem can also be applied in two dimensions, i.e. for image analysis. A 2D
sampling theorem has a simple physical interpretation in image analysis: Choose the sampling
interval such that it is less than or equal to half of the smallest interesting detail in the image.
The process of sampling
We start off with an analog signal. This can for example be the sound coming from your stereo at
home or your friend talking.
The signal is then sampled uniformly. Uniform sampling implies that we sample every Ts seconds.
In Figure 3.11 we see an analog signal. The analog signal has been sampled at times t= nTs .
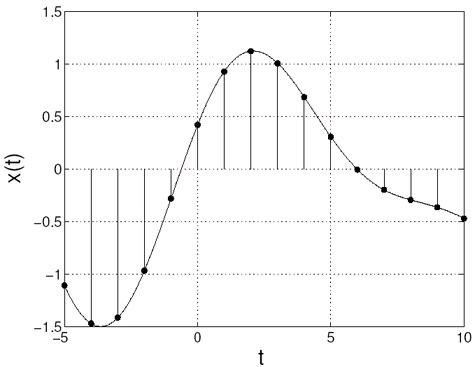
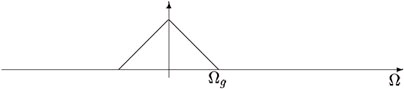


Figure 3.11.
Analog signal, samples are marked with dots.
In signal processing it is often more convenient and easier to work in the frequency domain. So
let's look at at the signal in frequency domain, Figure 3.12. For illustration purposes we take the
frequency content of the signal as a triangle. (If you Fourier transform the signal in Figure 3.11
you will not get such a nice triangle.)
Figure 3.12.
The spectrum X( ⅈΩ) .
Notice that the signal in Figure 3.12 is bandlimited. We can see that the signal is bandlimited
because X( ⅈΩ) is zero outside the interval [– Ωg, Ωg] . Equivalentely we can state that the signal has no angular frequencies above Ωg, corresponding to no frequencies above
.
Now let's take a look at the sampled signal in the frequency domain. While proving the sampling
theorem we found the the spectrum of the sampled signal consists of a sum of shifted versions of
the analog spectrum. Mathematically this is described by the following equation:
()
Sampling fast enough



In Figure 3.13 we show the result of sampling x( t) according to the sampling theorem. This means that when sampling the signal in Figure 3.11/Figure 3.12 we use Fs≥2 Fg . Observe in
Figure 3.13 that we have the same spectrum as in Figure 3.12 for Ω∈[-Ω



















































