Chapter 1. The Physics of Horn Playing
1.1. Acoustics for Music Theory*
Summary
For adults, a short review of the physics underlying music theory.
Music is Organized Sound Waves
Music is sound that's organized by people on purpose, to dance to, to tell a story, to make other people feel a certain way, or just to sound pretty or be entertaining. Music is organized on many different levels. Sounds can be arranged into melodies, harmonies, rhythms, textures and phrases. Beats, measures, cadences, and form all help to keep the music organized and understandable. But the most basic way that music is organized is by arranging the actual sound waves themselves so that the sounds are interesting and pleasant and go well together.
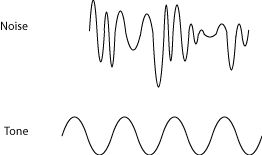
A rhythmic, organized set of thuds and crashes is perfectly good music - think of your favorite drum solo - but many musical instruments are designed specifically to produce the regular, evenly spaced sound waves that we hear as particular pitches. Crashes, thuds, and bangs are loud, short jumbles of lots of different wavelengths. These are the kinds of sound we often call "noise", when they're random and disorganized, but as soon as they are organized in time (rhythm), they begin to sound like music. (When used as a scientific term, noise refers to continuous sounds that are random mixtures of different wavelengths, not shorter crashes and thuds.)
However, to get the melodic kind of sounds more often associated with music, the sound waves must themselves be organized and regular, not random mixtures. Most of the sounds we hear are brought to our ears through the air. A movement of an object causes a disturbance of the normal motion of the air molecules near the object. Those molecules in turn disturb other nearby molecules out of their normal patterns of random motion, so that the disturbance itself becomes a thing that moves through the air - a sound wave. If the movement of the object is a fast, regular vibration, then the sound waves are also very regular. We hear such regular sound waves as tones, sounds with a particular pitch. It is this kind of sound that we most often associate with music, and that many musical instruments are designed to make.
Musicians have terms that they use to describe tones. (Musicians also have other meanings for the word "tone", but this course will stick to the "a sound with pitch" meaning.) This kind of (regular, evenly spaced) wave is useful for things other than music, however, so scientists and engineers also have terms that describe pitched sound waves. As we talk about where music theory comes from, it will be very useful to know both the scientific and the musical terms and how they are related to each other.
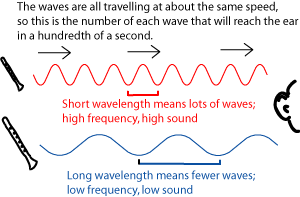
For example, the closer together those evenly-spaced waves are, the higher the note sounds. Musicians talk about the pitch of the sound, or name specific notes, or talk about tuning. Scientists and engineers, on the other hand, talk about the frequency and the wavelength of the sound. They are all essentially talking about the same things, but talking about them in slightly different ways, and using the scientific ideas of wavelength and frequency can help clarify some of the main ideas underlying music theory.
Longitudinal and Transverse Waves
So what are we talking about when we speak of sound waves? Waves are disturbances; they are changes in something - the surface of the ocean, the air, electromagnetic fields. Normally, these changes are travelling (except for standing waves); the disturbance is moving away from whatever created it, in a kind of domino effect.
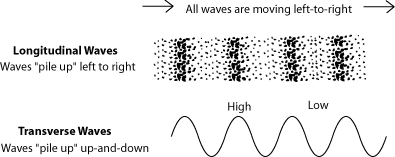
Most kinds of waves are transverse waves. In a transverse wave, as the wave is moving in one direction, it is creating a disturbance in a different direction. The most familiar example of this is waves on the surface of water. As the wave travels in one direction - say south - it is creating an up-and-down (not north-and-south) motion on the water's surface. This kind of wave is fairly easy to draw; a line going from left-to-right has up-and-down wiggles. (See Figure 1.2.)
But sound waves are not transverse. Sound waves are longitudinal waves. If sound waves are moving south, the disturbance that they are creating is giving the air molecules extra north-and-south (not east-and-west, or up-and-down) motion. If the disturbance is from a regular vibration, the result is that the molecules end up squeezed together into evenly-spaced waves. This is very difficult to show clearly in a diagram, so most diagrams, even diagrams of sound waves, show transverse waves.
Longitudinal waves may also be a little difficult to imagine, because there aren't any examples that we can see in everyday life (unless you like to play with toy slinkies). A mathematical description might be that in longitudinal waves, the waves (the disturbances) are along the same axis as the direction of motion of the wave; transverse waves are at right angles to the direction of motion of the wave. If this doesn't help, try imagining yourself as one of the particles that the wave is disturbing (a water drop on the surface of the ocean, or an air molecule). As it comes from behind you, a transverse waves lifts you up and then drops down; a longitudinal wave coming from behind pushes you forward and pulls you back. You can view here animations of longitudinal and transverse waves, single particles being disturbed by a transverse wave or by a longitudinal wave, and particles being disturbed by transverse and longitudinal waves.
The result of these "forward and backward" waves is that the "high point" of a sound wave is where the air molecules are bunched together, and the "low point" is where there are fewer air molecules. In a pitched sound, these areas of bunched molecules are very evenly spaced. In fact, they are so even, that there are some very useful things we can measure and say about them. In order to clearly show you what they are, most of the diagrams in this course will show sound waves as if they are transverse waves.
Wave Amplitude and Loudness
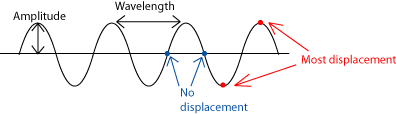
Both transverse and longitudinal waves cause a displacement of something: air molecules, for example, or the surface of the ocean. The amount of displacement at any particular spot changes as the wave passes. If there is no wave, or if the spot is in the same state it would be in if there was no wave, there is no displacement. Displacement is biggest (furthest from "normal") at the highest and lowest points of the wave. In a sound wave, then, there is no displacement wherever the air molecules are at a normal density. The most displacement occurs wherever the molecules are the most crowded or least crowded.
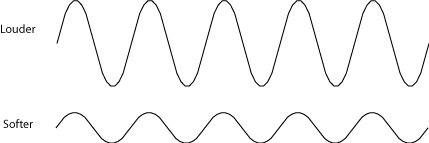
The amplitude of the wave is a measure of the displacement: how big is the change from no displacement to the peak of a wave? Are the waves on the lake two inches high or two feet? Are the air molecules bunched very tightly together, with very empty spaces between the waves, or are they barely more organized than they would be in their normal course of bouncing off of each other? Scientists measure the amplitude of sound waves in decibels. Leaves rustling in the wind are about 10 decibels; a jet engine is about 120 decibels.
Musicians call the loudness of a note its dynamic level. Forte (pronounced "FOR-tay") is a loud dynamic level; piano is soft. Dynamic levels don't correspond to a measured decibel level. An orchestra playing "fortissimo" (which basically means "even louder than forte") is going to be quite a bit louder than a string quartet playing "fortissimo". (See Dynamics for more of the terms that musicians use to talk about loudness.) Dynamics are more of a performance issue than a music theory issue, so amplitude doesn't need much discussion here.
Wavelength, Frequency, and Pitch
The aspect of evenly-spaced sound waves that really affects music theory is the spacing between the waves, the distance between, for example, one high point and the next high point. This is the wavelength, and it affects the pitch of the sound; the closer together the waves are, the higher the tone sounds.
All sound waves are travelling at about the same speed - the speed of sound. So waves with a shorter wavelength arrive (at your ear, for example) more often (frequently) than longer waves. This aspect of a sound - how often a peak of a wave goes by, is called frequency by scientists and engineers. They measure it in hertz, which is how many peaks go by per second. People can hear sounds that range from about 20 to about 17,000 hertz.
The word that musicians use for frequency is pitch. The shorter the wavelength, the higher the frequency, and the higher the pitch, of the sound. In other words, short waves sound high; long waves sound low. Instead of measuring frequencies, musicians name the pitches that they use most often. They might call a note "middle C" or "second line G" or "the F sharp in the bass clef". (See Octaves and Diatonic Music and Tuning Systems for more on naming specific frequencies.) These notes have frequencies (Have you heard of the "A 440" that is used as a tuning note?), but the actual frequency of a middle C can vary a little from one orchestra, piano, or performance, to another, so musicians usually find it more useful to talk about note names.
Most musicians cannot name the frequencies of any notes other than the tuning A (440 hertz). The human ear can easily distinguish two pitches that are only one hertz apart when it hears them both, but it is the very rare musician who can hear specifically that a note is 442 hertz rather than 440. So why should we bother talking about frequency, when musicians usually don't? As we will see, the physics of sound waves - and especially frequency - affects the most basic aspects of music, including pitch, tuning, consonance and dissonance, harmony, and timbre.
1.2. Standing Waves and Wind Instruments*
Summary
The musical sounds of aerophones (woodwinds and brass) are created by standing waves in the air inside the instruments.
A wind instrument makes a tone when a standing wave of air is created inside it. In most wind instruments, a vibration that the player makes at the mouthpiece is picked up and amplified and given a pleasant timbre by the air inside the tube-shaped body of the instrument. The shape and length of the inside of the tube give the sound wave its pitch as well as its timbre.
You will find below a discussion of what makes standing waves in a tube, wind instruments and the harmonic series, and the types of tubes that can be used in musical instruments. This is a simplified discussion to give you a basic idea of what's going on inside a wind instrument. Mathematical equations are avoided, and all the complications - for example, what happens to the wave when there are closed finger holes in the side of the tube - are ignored. Actually, the physics of what happens inside real wind instruments is so complex that physicists are still studying it, and still don't have all the answers. If you want a more in-depth or more technical discussion, there are some recommendations below.
If you can't follow the discussion below, try reviewing Acoustics for Music Theory, Standing Waves and Musical Instruments, Harmonic Series I, and Wind Instruments: Some Basics
What Makes the Standing Waves in a Tube
As discussed in Standing Waves and Musical Instruments, instruments produce musical tones by trapping waves of specific lengths in the instrument. It's pretty easy to see why the standing waves on a string can only have certain lengths; since the ends of the strings are held in place, there has to be a node in the wave at each end. But what is it that makes only certain standing waves possible in a tube of air?
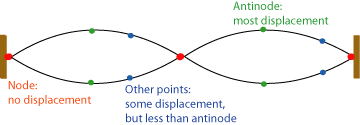
To understand that, you'll have to understand a little bit about what makes waves in a tube different from waves on a string. Waves on a string are transverse waves. The string is stretched out in one direction (call it "up and down"), but when it's vibrating, the motion of the string is in a different direction (call it "back and forth"). Take a look at this animation. At the nodes (each end, for example), there is no back and forth motion, but in between the nodes, the string is moving back and forth very rapidly. The term for this back-and-forth motion is displacement. There is no displacement at a node; the most displacement happens at an antinode.
The standing waves of air in a tube are not transverse waves. Like all sound waves, they are longitudinal. So if the air in the tube is moving in a certain direction (call it "left and right"), the vibrations in the air are going in that same direction (in this case, they are rushing "left and right").
But they are like the waves on a string in some important ways. Since they are standing waves, there are still nodes - in this case, places where the air is not rushing back and forth. And, just as on the string, in between the nodes there are antinodes, where the displacement is largest (the air is moving back and forth the most). And when one antinode is going in one direction (left), the antinodes nearest it will be going in the other direction (right). So, even though what is happening is very different, the end result of standing waves "trapped" in a tube will be very much like the end result of standing waves "trapped" on a string: a harmonic series based on the tube length.
There will be more on that harmonic series in the next section. First, let's talk about why only some standing waves will "fit" in a tube of a particular length. If the tube were closed on both ends, it's easy to see that this would be a lot like the wave on the string. The air would not be able to rush back and forth at the ends, so any wave trapped inside this tube would have to have nodes at each end.
It's very difficult to draw air that is rushing back and forth in some places and standing still in other places, so most of the figures below use a common illustration method, showing the longitudinal waves as if they are simultaneously the two maximum positions of a transverse wave. Here is an animation that may give you some idea of what is happening in a longitudinal standing wave. As of this writing, there was a nice Standing Waves applet demonstration of waves in tubes. Also, see below for more explanation of what the transverse waves inside the tubes really represent.
Now, a closed tube wouldn't make a very good musical instrument; it wouldn't be very loud. Most of the sound you hear from an instrument is not the standing wave inside the tube; the sound is made at the open ends where the standing waves manage to create other waves that can move away from the instrument. Physicists sometimes study the acoustics of a tube closed at both ends (called a Kundt tube), but most wind instruments have at least one open end. An instrument that is open at both ends may be called open-open, or just an open tube instrument. An instrument that is only open at one end may be called open-closed, or a closed tube or stopped tube instrument (or sometimes semi-closed or half-closed). This is a little confusing, since such instruments (trumpets, for example) still obviously have one open end.
Now, there's nothing stopping the air from rushing back and forth at the open end of the tube. In fact, the waves that "fit" the tube are the ones that have antinodes at the open end, so the air is in fact rushing back and forth there, causing waves (at the same frequency as the standing wave) that are not trapped in the instrument but can go out into the room.