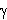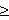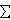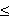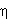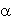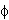3. SYSTEM
System Analytics
Agents: Doctors, scientists, system analysts, business analysts, engineers;
Moves : requirements engineering, system design, prototype testing, installation, testing, commissioning;
Emerging technologies: innovate a set of emerging technologies based on health security parameters and sustainable development goals.
 Proactive approach
Proactive approach
 Reactive approach
Reactive approach
 Deep learning /* multi-model ensembling method */
Deep learning /* multi-model ensembling method */
-
-
- Raw data collection
- Data filtering
- Feature selection
- Cross validation
- Configure deep learning architecture
- Define training strategy(algorithm, learning rate, stopping criteria);
- Call 1st stage classification algorithm
- Call 2nd stage ensemble method
- Testing strategy KDD
 Intelligent reasoning
Intelligent reasoning
-
-
- Case based reasoning
- Perception common sense reasoning
 Regenerative medicine
Regenerative medicine
 Precision medicine
Precision medicine
 Cancer genomics
Cancer genomics
-
- Biomedical technology: artificial pancreas, artificial liver, artificial kidney, artificial limbs, artificial cardiovascular devices, oral insulin;
- Artificial immune system for epidemic and pandemic control.
Dr, Jim Morrison and Prof. Michel Bolton are presenting on emerging healthcare systems. Artificial intelligence (AI) is basically simulation of human intelligence. An intelligent reasoning system demands new data structure beyond knowledge base with envision, perception and proper assessment of a problem; reasoning is not effective when done in isolation from its significance in terms of the needs and interests of an agent with respect to the wider world. A rational reasoning system needs the support of an intelligent analytics. The basic objective is to evaluate the natural and adaptive immunity of a complex system. The evaluation of the immunity of a system involves modeling, defining complete specifications and verification.
First, it is essential to model the human biological system by proper representation of its various states and programs. Next, it is important to specify the properties of the system through logical reasoning. Finally, it is essential to develop a verification mechanism which justifies: does the model satisfy the properties indicating a healthy immune system? The evaluation of immunity of a system can be done by exhaustive search of the state space (local, global, initial and goal states and state transition relations) of a system through simulation, testing, deductive reasoning and model checking based on intelligent search. The procedure terminates with positive or negative answer; the positive answer indicates a healthy immune system; the negative results provide an error trace indicating incorrect modeling or specification of the system or the occurrence of malicious threats.
The human immune system is an adaptive, robust, complex and distributed information processing system which protects the health of the biological system from the attacks of malicious foreign pathogens (e.g. virus, bacteria, fungi, protozoa, parasitic worms). It discriminates the self from non-self elements. The immunity is either innate or adaptive; innate immunity detects and kills specific known invading organisms; adaptive immunity responds to previously unknown foreign organisms. AI community needs a new outlook, imagination and dreams to solve a complex problem like prevention of cancer through a set of simple mechanisms. There are some types of cancer due to bad luck. But, we still do not know enough about the causes and preventive measures of different types of cancer. The following section highlights two branches of artificial intelligence: (a) deep learning and (b) case based reasoning.
Deep Learning : Cancer is a complex global health problem involving abnormal cell growth and a major cause of morbidity and mortality. It is challenging to predict cancer using machine learning algorithms based on gene expression or image data for effective and accurate decision making, diagnosis and detection at early stage. It is basically a classification problem which predicts and distinguishes cancer patients from healthy persons. Recently, deep learning has been explored in terms of ensemble approach that combines multiple machine learning models. It is an interesting strategic option to apply various classification algorithms on informative gene expression and then a deep learning approach is employed to ensemble the outputs of the classifiers. This deep learning based multi-model ensemble method is an accurate and effective method for cancer prediction as compared to single classifier. One of the critical issues is that it is irrational to mix data of various types of cancer and then apply deep learning based multi-model ensemble method on this mixed data. Rather, it is correct to apply deep learning algorithm on data set of different types of cancer separately such as lung, stomach and breast cancer.
Let us exercise SWOT analysis on deep learning. Deep learning is an efficient biomedical research tool in many potential applications such as drug discovery and biomarker development. A neural network may have a single hidden layer where DNN has many hierarchical layers of nonlinear information processing units. A simple neural network does not deal well with raw data whereas deep learning can be largely unsupervised and can learn intricate patterns from even high- dimensional raw data with little guidance. Only a deep circuit can perform exponentially complex computational tasks without requiring an infinite number of nodes. DNNs can process very large high dimensional, sparse, noisy data sets with nonlinear relationships. DNNs have high generalization ability; once trained on a data set, they can be applied to other new data sets; this is a requirement for binding and interpretation of heterogeneous multiplatform data. DNNs can be classified into networks for unsupervised learning, networks for supervised learning and hybrid or semi-supervised networks.
But there are some limitations such as black box problem in quality control and interpretation of high dimensional data; selection problem in choosing appropriate DNN architecture, high computational cost of time consuming training method, overfitting problem and the need for large training data sets that may not be readily available. In case of overfitting, training error is low but the test error is high.
Training strategy : Data analysis on gene expression level is one of the research hotspots today. There are various types of machine learning algorithm such as k - nearest-neighbor (kNN), support vector machines (SVM), decision trees (DT), random forests (RF), and gradient boosting decision trees (GBDT). But, each machine learning method has its own flaws in terms of classification accuracy and other performance measures. It is hard for SVM to find out an appropriate kernel function. DTs have over fitting problems and RFs require more samples to attain high classification accuracy. Each machine learning algorithm may outperform others; it is rational to adopt multiple learning algorithms for better performance. There are various types of ensemble methods such as bagging, boosting, linear regression, stacking, majority voting algorithm and deep learning. Majority voting considers linear relationships among classifiers.
Deep learning has the ability to learn the intricate nonlinear structures from the original large data sets automatically. Deep neural networks can ensemble multiple classification models to predict cancer more accurately. To avoid over fitting, it is required to preprocess the raw data and employ differential gene expression analysis to select important and informative genes, which are fed to various classification models. A deep neural network is used to ensemble the outputs of multiple classification models to obtain the final prediction result. Deep learning based multi-model ensemble method makes more effective use of the information of the limited cancer data and generates more accurate prediction than single classifiers or majority voting algorithm. There are several open issues. Is it rational to ensemble the outputs of multiple classification models to obtain the final prediction result for same type of cancer across different demographic profile of cancer patients or various zones of the world? Is it possible to ensemble the outputs of multiple classifiers for different types of cancer?
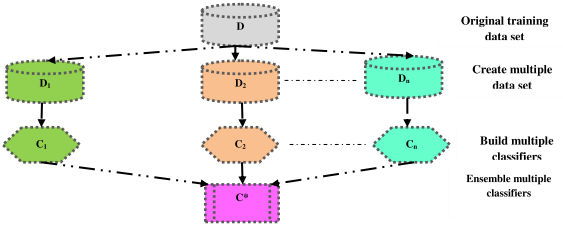
Figure 5.1. Ensemble learning method
Another critical issue is to improve classification accuracy in case of imbalanced, multi-class learning problems. Let us consider the case of bowel cancer data where a large number of examples of normal cases may exist with a much smaller number of positive cases of cancer. This data imbalance complicates the learning process and may result misclassification for the classes with fewer representative examples. Such uneven distribution may create a difficult learning process for finding unbiased decision boundaries. A regularized ensemble model of deep learning employs regularization that accommodates multiclass data sets, automatically determines error bound and penalizes the classifier when it misclassifies examples that were correctly classified in the previous learning phase and can attain superior performance in terms of improvement of overall accuracy for all classes.
Testing strategy: Let us consider three data sets of three kinds of cancers such as Lung cancer (LCD), Stomach cancer (SCD) and Breast cancer data (BCD).
-
-
- ROC curve for LCD : True positive rate vs. false positive rate for KNN, SVM, DT,RF, Majority voting, ensemble
- ROC curve for SCD data
- ROC curve for BCDA data
- Dataset, data size, precision (%), recall (%), accuracy(%), CPU time(S)
- Predictive accuracy (%) of various classification algorithms
Optimal Margin Classifier for Cancer Detection : The expert panel are trying to explore whether an efficient optimal margin classifier such as support vector machine can be applicable for detection of cancer. Here, the most important issue is the performance of SVM in terms of classification accuracy and privacy of data. Classification comprises of two subtasks: learning a classifier from training data with class labels and predicting the class labels for unlabeled data using the learned classifier. Data can be stored as feature vectors. In the classification problem of detecting cancer, the training data comprises of patients with labels cancer or no cancer. Support Vector Machine (SVM) is the most well-known kernelized maximum margin classifier. The learning methodology is the approach of using examples to synthesis programs for computing the desired output from a set of inputs; it generates target decision function in hypothesis space. The learning algorithm selects training data as input and selects a hypothesis from the hypothesis space. There are various methods of learning such as supervised learning from training examples, unsupervised learning, batch learning and online learning. The next issue is generalization - how to assess the quality of an online learning algorithm? Consistent hypothesis performs correct classification of the training data. The ability of a learning machine to correctly classify data not existing in the training set is known as generalization. How to improve generalization: Ockham’s Razor suggests that unnecessary complications are not helpful; it may result overfit. Support Vector Machine (SVM) is a learning system that uses a hypothesis space of linear functions in a high dimensional feature space, trained with a learning algorithm from optimization theory that implements a learning bias derived from statistical learning theory. In case of pattern classification problem, the objective of SVM is to devise a computationally efficient way of learning for finding out an optimal capacity of the pattern classifier to minimize the expected generalization error on a given amount of training data by maximizing the margin between training patterns and class boundary. The basic properties of SVM are that the learning system is suitable for both linear and nonlinear problems, computationally efficient algorithm through modular and dual representation in Kernel induced high dimensional feature space and optimized generalization bounds.
Learning in Kernel induced feature space is as follows:
Target Function – f(m1,m2,r) = C*m1*m2/r2; g(x,y,z) = ln f(m1,m2,r) = ln C+ ln m1 + ln m2 -2 ln r = c+x+y-2z; A linear machine can learn g but not f. A kernel is a function K such that for all x,z ε X ;K(x,z) = <φ(x). φ(z)> where φ is a mapping from input space X to inner product feature space F.
<x.z>2 = (Σn i=1 xi zi)2 = (Σn i=1 xi zi) (Σn j=1 xj zj) = Σn i=1 Σn j=1 xi zi xj zj = Σn,n i,j=(1,1) (xi xj ) ( zj zi ) = φ(x). φ(z)
Let us consider linear classification problem. Given a linearly separable training sample S = ((x1, y1), , (xl , yl)), the hyperplane (w,b) realizes the maximal margin hyperplane with geometric margin 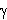 = 1/ ||w||2 by solving the optimization problem : Minimize <w.w> Subject to yi (
= 1/ ||w||2 by solving the optimization problem : Minimize <w.w> Subject to yi (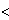 w. xi
w. xi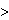 + b)
+ b) 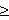 1 where i = 1,. ,l; In case of SVM, the strategy is to find the maximal margin hyperplane in kernel induced feature space. In case of linear classification problem, the equation of hyperplane is f(x) =
1 where i = 1,. ,l; In case of SVM, the strategy is to find the maximal margin hyperplane in kernel induced feature space. In case of linear classification problem, the equation of hyperplane is f(x) = 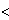 w.x
w.x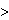 +b = 0 or, f(x) =
+b = 0 or, f(x) = 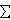 li=1 wi xi +b = 0; An input x = (x1, , xn) belongs to positive class if f(x)
li=1 wi xi +b = 0; An input x = (x1, , xn) belongs to positive class if f(x) 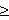 0; An input x = (x1,...., xn) belongs to negative class if f(x) < 0. The decision function: h(x) = sgn (f(x)) = sgn(
0; An input x = (x1,...., xn) belongs to negative class if f(x) < 0. The decision function: h(x) = sgn (f(x)) = sgn(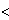 w.x
w.x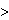 +b); Functional margin of an example (xi, yi) is
+b); Functional margin of an example (xi, yi) is 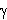 i = yi (
i = yi (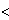 w.xi
w.xi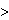 + b). Geometric margin measures the Euclidean distance between an example and the hyperplane, it is expressed as normalized linear function (w/ ||w||, b/ ||w||). Updation rule of SVM algorithm in primal form is as follows: if
+ b). Geometric margin measures the Euclidean distance between an example and the hyperplane, it is expressed as normalized linear function (w/ ||w||, b/ ||w||). Updation rule of SVM algorithm in primal form is as follows: if 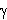 i or yi (
i or yi (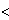 w.xi
w.xi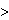 + b)
+ b) 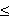 0 then wk+1
0 then wk+1 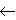 wk +
wk + 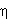 yixi , k
yixi , k 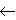 k+1
k+1 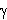 i
i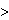 0 indicates correct classification of the training example. Duality is the one of the basic features of Support Vector Machine; SVMs can be modelled as linear learning machines in a dual fashion. In this case, updation rule of the perceptron algorithm is expressed in dual form. The solution i.e. final hypothesis of weight vector is a linear combination of training points. Each pattern xi is associated with an embedding strength
0 indicates correct classification of the training example. Duality is the one of the basic features of Support Vector Machine; SVMs can be modelled as linear learning machines in a dual fashion. In this case, updation rule of the perceptron algorithm is expressed in dual form. The solution i.e. final hypothesis of weight vector is a linear combination of training points. Each pattern xi is associated with an embedding strength 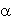 i , which is proportional to the no. of times misclassification of xi causes updation of the weight.
i , which is proportional to the no. of times misclassification of xi causes updation of the weight.
w = 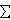 li=1
li=1 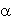 i yi xi
i yi xi
f(x) = 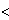 w.x
w.x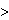 +b = 0
+b = 0
= (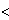
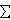 li=1
li=1 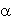 i yi xi.x
i yi xi.x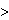 +b )
+b )
= (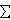 li=1
li=1 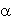 i yi
i yi 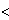 xi.x
xi.x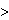 +b )
+b )
In the dual form, the updation rule and decision function can be expressed in the form of inner product space 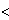 xi.x
xi.x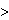 .
.
Kernel Based Algorithms; Two separate learning functions; Learning Algorithm in an embedded space; Kernel function performs the embedding; Embed data to a different space; Possibly higher dimension; Linearly separable in the new space. Kernels themselves can be constructed in a modular way. Modularity is one of the important properties of SVM.
Learning In Kernel Induced Feature Space : Kernel methods exploit information about the inner products between data items. Kernel function can simplify the computation of separating hyperplane without explicitly carrying out the map in the feature space. The number of operations to compute the inner product space is not proportional to the number of features. Hence, high dimension of feature space does not affect the computation. Since F is high dimensional, the RHS of this equation is computationally very expensive.
f(x) = 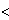 w.x
w.x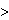 +b = (
+b = (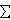 l
l 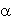 i yi
i yi 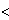 xi.x
xi.x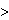 +b ); it is the equation of hyperplane in input space. f(x) =
+b ); it is the equation of hyperplane in input space. f(x) = 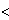 w.
w. 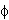 (x)
(x)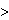 +b = (
+b = (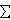 li=1
li=1 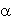 i yi
i yi 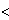
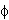 (xi).
(xi). 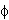 (x)
(x)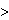 + b ); it is the equation of hyperplane in feature space where
+ b ); it is the equation of hyperplane in feature space where 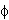 is a mapping from input space to inner product feature space. f(x) =
is a mapping from input space to inner product feature space. f(x) = 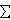 li=1
li=1 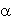 i yi K (xi.x) + b where K = Kernel function Next, let us consider computation of geometric margin. Geometric margin is the functional margin of a normalized weight vector. In case of linear classifier, the hyperplane function (w,b) does not change if we rescale the hyperplane (mw,mb) where m
i yi K (xi.x) + b where K = Kernel function Next, let us consider computation of geometric margin. Geometric margin is the functional margin of a normalized weight vector. In case of linear classifier, the hyperplane function (w,b) does not change if we rescale the hyperplane (mw,mb) where m 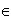 R+ due to inherent degree of freedom. So, to optimize the geometric margin, we can consider functional margin of 1 for two points x+ and x - .
R+ due to inherent degree of freedom. So, to optimize the geometric margin, we can consider functional margin of 1 for two points x+ and x - . 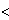 w.x+
w.x+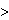 +b = +1;
+b = +1; 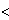 w.x -
w.x -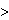 +b = -1; Geometric margin
+b = -1; Geometric margin 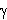 = ½(||w||2) [(
= ½(||w||2) [(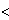 w.x+
w.x+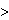 +b) – (
+b) – (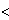 w.x -
w.x -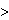 +b)] =1/ ||w||2.
+b)] =1/ ||w||2.
SVM problem formulation is as follows. Given a linearly separable training sample S = ((x1, y1), ....., (xl, yl)), the hyperplane (w,b) realizes the maximal margin hyperplane with geometric margin 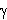 = 1/ ||w||2 by solving the optimization problem - minimize <w.w> subject to yi (
= 1/ ||w||2 by solving the optimization problem - minimize <w.w> subject to yi (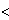 w. xi
w. xi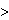 + b)
+ b) 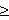 1 where i = 1,....,l; this is a convex optimization problem minimizing a quadratic function under linear inequality constraints.
1 where i = 1,....,l; this is a convex optimization problem minimizing a quadratic function under linear inequality constraints.
Primal Form ---- L(w, b,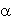 ) = 1/2
) = 1/2