Fig. 10. Model with counterweights mass Fig. 11. Balanced Hexapod using pantograph
Fig. 12. Leg counterweight
In this case, the mass M becomes,
6
6
∗
∗
∗
M = m + m + m + m +
m +
p
p
a
a
∑ i ∑ im
(82)
i= 1
i= 1
Dynamics of Hexapods with Fixed-Length Legs
263
where mp and ∗
mp are the mass of the platform and the mass of the platform counterweight,
i
m and ∗ i
m are the mass of the legs and the mass of the legs counterweights, a
m and ∗ a
m are
the mass of the pantograph and the mass of the of the pantograph counterweight. In this
case, the global center of the mass of the manipulator is written as
6
6
Mr = m
∗ ∗
∗ ∗
∗ ∗
r +
r +
r +
r +
r +
∑
∑
p p
mp p ma a ma a
i
m i
i
m ir
(83)
i= 1
i= 1
where
∗
p
r and pr are the platform center of the mass and the platform counterweight
position,
∗
i
r and ir are the legs center of the mass and the legs counterweight position,
∗
a
r and ar are the pantograph center of the mass and the pantograph counterweight position.
From Figs. 9-10, vectors
∗
∗
∗
r
p
r , pr , ar , ar , ir and i can be derived and substituted into eq.(83), yielding
∗
r =
(h + Q ⋅g)
⎛
⎞
⎛
⎞
∗
∗
l
∗
l
M
m
+ m (h + Q ⋅ g )
a
a
+
⎜ h
⎟ +
⎜ h
⎟ +
p
p
ma
ma
⎜
⎟
⎜
⎟
⎝ h ⎠
⎝ h ⎠
6
⎡
l ⎤
+∑ m ⎢(h + Q ⋅p ) −(h + Q ⋅p − b − s ) gi ⎥ +
i
i
i
i
i
(84)
⎣
l
i= 1
i ⎦
6
∗
⎡
⎤
+∑ m∗ ⎢(h + Q ⋅p ) − (h + Q ⋅p − b − s ) lgi
i
i
i
i
i
⎥
⎢
l
i= 1
i ⎥
⎣
⎦
where, la is the center of mass of the pantograph with respect to the fixed frame, la* is the
pantograph counterweight position with respect to the fixed frame, lgi is the length of the leg
counterweight link, li is the length of the leg, s i can be written, for i= 1,...,6, as
s = ρ ⋅ ˆ
i
i s i
(85)
In concise form, eq.(84) can be expressed as
Mr = A h + QB +
A s +
∑6
1
5 i i
A0
(86)
i= 1
where
∗
∗
6
l
l
⎛
lgi ⎞
6
⎛
l ⎞
∗
∗
∗
A = m + m + m
+ m
+
1
p
p
a
a
∑ im⎜ 1− ⎟+ m ⎜ 1− gi
a
a
⎟
∑ i
(87)
h
h
l
⎜
l ⎟
i= 1
⎝
i ⎠
i= 1
⎝
i ⎠
∗
6
⎛
lgi ⎞
6
⎛
l ⎞
∗ ∗
∗
B = m g + m g +
p
p
∑ imp i⎜ 1− ⎟+ m p ⎜ 1− gi ⎟
∑ i i
(88)
l
⎜
l ⎟
i= 1
⎝
i ⎠
i= 1
⎝
i ⎠
l
l∗
gi
∗ gi
=
+
5
A i
i
m
i
m
, i=1,..,6
(89)
i
l
i
l
264
Parallel Manipulators, Towards New Applications
A =
0
∑6 5
A ib i
(90)
i= 1
The conditions for static balancing can be given, for i = 1,..,6, as follows
A =
1
0 , B = 0 , A =
i
0 , A =
5
0
0
(91)
From conditions A =
5 i
0 , for i=1,..,6, one can obtain
∗
l
l
gi
∗
m
+
gi
m
=
i
i
0
(92)
i
l
i
l
From eq. (92), for i= 1,..,6 , the following is obtained
m l
∗
l = − i gi
gi
(93)
∗ i
m
By condition
=
1
A
0 , i.e.,
6
∗
∗
l
∗ l∗
a
a
m +
+
+
+
+
=
∑
p
mp
( i
m
i
m ) ma
ma
0
(94)
h
h
i= 1
one can obtain
h ⎛
6
l ⎞
*
l = −
⎜ m + *
m +
*
a
a
m
m
m
(95)
*
p
p
∑( +
i
i ) +
a
⎟
⎜
⎟
a
m ⎝
h
i= 1
⎠
Finally, condition B = 0 leads to the following
∗
∗
m g + m g +
(
∗
m + m )p =
∑ 6
p
p
i
i
i
0
(96)
i= 1
Eq.(96) shows that the static balancing can be achieved by fixing the global center of the
mass of the moving platform, that of the legs and their counterweights at the same position,
O'. In order to obtain it, the platform counterweight should be placed in the position:
m g + ∑ 6
p
(
∗
m +
i
i
m )p i
∗
i=
g =
1
(97)
∗
mp
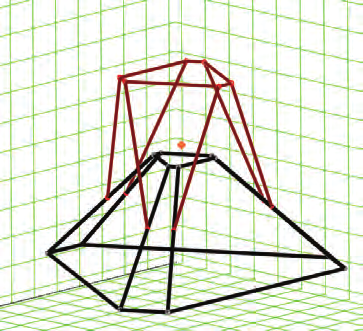
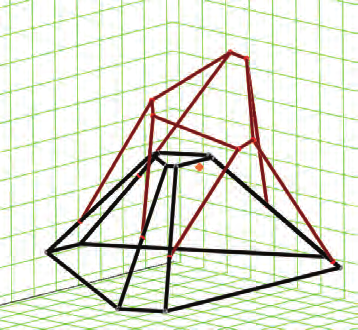
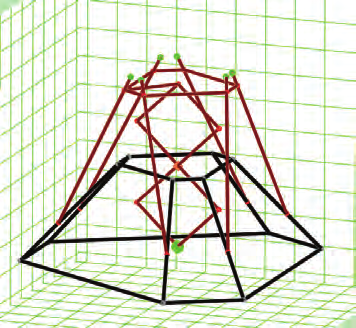
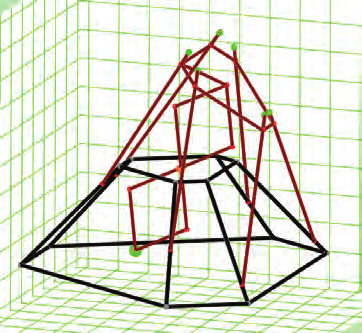
Simulation is carried out to demonstrate the proposed method. The results are shown in
Figs. 13-14, from which it can be seen that the centre of mass of the robot is non-stationary
for non balanced case, while it is fixed for the balanced case.
After static balancing the global mass of the device increases by
∗
∗
∗
Δ M = m + m + m + ∑ 6
p
a
a
i
m
(98)
i= 1
Dynamics of Hexapods with Fixed-Length Legs
265
The negative effect for the dynamic performance by the increasing global mass can be
reduced by optimum design of the pantograph. A graph can be arranged to provide such
help. Fig. 15 shows the ratios,
M + Δ M I + *
I
I +
*
I
, i
i , a
a
,
(99)
M
Ii
I a
which vary respect to the ratio ra*/ h and lgi*/ lgi and where Ii is the moment of inertia of the
leg, Ii* is the moment of inertia of the leg counterweight whit respect of P i, Ia is the moment
of inertia of the moving platform and Ia* is the moment of inertia of the pantograph
counterweight with respect of O. It should be noted that with a suitable design it is possible
to reduce M
Δ at the same time, it may increase Ii and Ia. The effect of gravity compensation
on the dynamic performances was studied in detail in (Xi, 1999).
Fig. 13. Mobile center of mass Hexapod
Fig. 14. Fixed center of mass of Balanced Hexapod

266
Parallel Manipulators, Towards New Applications
Figure 15. Graph for optimum design
Input
Mobile platform
mass [kg]
short side [mm] long side [mm]
8 200
800
Fixed platform 1
mass [kg]
short side [mm] long side [mm]
/ 100
400
Fixed platform 2
mass [kg]
short side [mm] long side [mm]
/ 250
1000
leg
mass [kg]
li [mm]
lgi [mm]
0.5 750
375
Pantograph
mass [kg]
side length [mm]
ra [mm]
3 100
0
Output
m a* [kg]
mi* [kg]
17 1
Table 3. Geometric and inertial parameters
Dynamics of Hexapods with Fixed-Length Legs
267
7. Conclusion
In this chapter, the inverse dynamics of hexapods with fixed-length legs is analyzed using
the natural orthogonal complement method, with considering the mass of the moving
platform and those of the legs. A complete kinematics model is developed, which leads to
an explicit expression for the twist-mapping matrix. Based on that, the inverse dynamics
equations are derived that can be used to compute the required applied actuator forces for
the given movement of the moving platform. The developed method has been implemented
and demonstrated by simulation.
Successively, the static balancing of hexapods is addressed. The expression of the global
center of mass is derived, based on which a set of static balancing equations has been
obtained. It is shown that this type of parallel mechanism cannot be statically balanced by
counterweights because prismatic joints do not have a fixed point to pivot as revolute joints.
A new design is proposed to connect the centre of the moving platform to that of the fixed
platform by a pantograph. The conditions for static balancing are derived. This mechanism
is able to release the actuated joints from the weight of the moving legs for any
configurations of the robot.
In the future research the leg inertia will be include for modeling the dynamics of the
hexapod for high-speed applications.
8. References
Angeles, J. & Lee, S. (1988). The Formulation of Dynamical Equations of Holonomic
Mechanical Systems Using a Natural Orthogonal Complement, ASME J. Applied
Mechanics, Vol. 55, pp. 243-244, ISSN: 0021-8936
Angeles, J. & Lee, S. (1989). The Modeling of Holonomic Mechanical Systems Using a
Natural Orthogonal Complement, Trans. Canadian Society of Mechanical Engineering,
Vol. 13, No. 4, pp. 81-89, ISSN: 0315-8977
Angeles, J. & Ma, O. (1988). Dynamic Simulation of n-axis Serial Robotic Manipulators
Using a Natural Orthogonal Complement, The International Journal of Robotics
Research, Vol. 7, No. 5, pp. 32-47, ISSN: 0278-3649
Do, W. Q. D. & Yang, D. C. H. (1988). Inverse Dynamics and Simulation of a Platform Type
of Robot, The International Journal of Robotics Research, Vol. 5, No. 3, pp. 209-227,
ISSN: 0278-3649
Fichter, E. F. (1986). A Stewart Platform-based Manipulator: General Theory and Practical
Construction, The International Journal of Robotics Research, Vol. 5, No. 2, pp. 157-182,
ISSN: 0278-3649
Fijany, A., & Bejezy, A. K., (1991). Parallel Computation of Manipulator Inverse Dynamics,
Journal of Robotic Systems, Vol. 8, No. 5, pp. 599-635, ISSN: 0741-2223
Geng, Z.; Haynes, L. S.; Lee, T. D. & Carroll, R. L. (1992). On the Dynamic and Kinematic
Analysis of a Class of Stewart Platforms, Robotics and Autonomous Systems, Vol. 9,
No. 4, pp. 237-254, ISSN: 0921-8890
Gosselin, C. M. & Wang, J. (1998). On the design of gravity-compensated six-degree-of-
freedom parallel mechanisms, Proceedings of IEEE International Conference on Robotics
and Automation, Leuven, Belgium, May 1998, ISBN: 0-7803-4300-X
Hashimoto, K. and Kimura, H., (1989). A New Parallel Algorithm for Inverse Dynamics, The
International Journal of Robotics Research, Vol. 8, No. 1, pp. 63-76, ISSN: 0278-3649
Hervé, J. M. (1986). Device for counter-balancing the forces due to gravity in a robot arm,
United States Patent, 4,620,829
268








