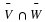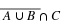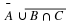Find the indicated sets.
List all subsets of the following set.
List all subsets of the following set.
List the elements of the following set.
List the elements of the following set.
In Problems 5 - 8, let Universal set=U={a,b,c,d,e,f,g,h,i,j}, V={a,e,i,f,h}, and W={a,c,e,g,i}.
List the members of the following sets.
In 9 - 12, let Universal set=U={1,2,3,4,5,6,7,8,9,10}, A={1,2,3,4,5}, B={1,3,4,6}, and C={2,4,6}.
List the members of the following sets.
Find the number of elements in the following sets.
In Mrs. Yamamoto's class of 35 students, 12 students are taking history, 18 are taking English, and 4 are taking both. Draw a Venn diagram and determine how many students are taking neither history nor English?
In the County of Santa Clara 700,000 people read the San Jose Mercury News, 400,000 people read the San Francisco Examiner, and 100,000 read both newspapers. How many read either the Mercury News or the Examiner?
A survey of athletes revealed that for their minor aches and pains, 30 used aspirin, 50 used ibuprofen, and 15 used both. How many athletes were surveyed?
In a survey of computer users, it was found that 50 use HP printers, 30 use IBM printers, 20 use Apple printers, 13 use HP and IBM, 9 use HP and Apple, 7 use IBM and Apple, and 3 use all three. How many use at least one of these Brands?
This quarter, a survey of 100 students at De Anza college finds that 50 take math, 40 take English, and 30 take history. Of these 15 take English and math, 10 take English and history, 10 take math and history, and 5 take all three subjects. Draw a Venn diagram and determine the following.
The number of students taking math but not the other two subjects.
The number of students taking English or math but not history.
The number of students taking none of these subjects.
30
60
10
In a survey of investors it was found that 100 invested in stocks, 60 in mutual funds, and 50 in bonds. Of these, 35 invested in stocks and mutual funds, 30 in mutual funds and bonds, 28 in stocks and bonds, and 20 in all three. Determine the following.
The number of investors that participated in the survey.
How many invested in stocks or mutual funds but not in bonds?
How many invested in exactly one type of investment?
Do the following problems using a tree diagram or the multiplcation axiom.
A man has 3 shirts, and 2 pairs of pants. Use a tree diagram to determine the number of possible outfits.
In a city election, there are 2 candidates for mayor, and 3 for supervisor. Use a tree diagram to find the number of ways to fill the two offices.
There are 4 roads from Town A to Town B, 2 roads from Town B to Town C. Use a tree diagram to find the number of ways one can travel from Town A to Town C.
Brown Home Construction offers a selection of 3 floor plans, 2 roof types, and 2 exterior wall types. Use a tree diagram to determine the number of possible homes available.
For lunch, a small restaurant offers 2 types of soups, three kinds of sandwiches, and two types of soft drinks. Use a tree diagram to determine the number of possible meals consisting of a soup, sandwich, and a soft drink.
A California license plate consists of a number from 1 to 5, then three letters followed by three digits. How many such plates are possible?
A license plate consists of three letters followed by three digits. How many license plates are possible if no letter may be repeated?
How many different 4-letter radio station call letters can be made if the first letter must be K or W and none of the letters may be repeated?
How many seven-digit telephone numbers are possible if the first two digits cannot be ones or zeros?
How many 3-letter word sequences can be formed using the letters {a,b,c,d} if no letter is to be repeated?
A family has two children, use a tree diagram to determine all four possibilities.
A coin is tossed three times and the sequence of heads and tails is recorded. Use a tree diagram to determine the different possibilities.
In how many ways can a 4-question true-false test be answered?
In how many ways can three people be made to stand in a straight line?
A combination lock is opened by first turning to the left, then to the right, and then to the left again. If there are 30 digits on the dial, how many possible combinations are there?
How many different answers are possible for a multiple-choice test with 10 questions and five possible answers for each question?
Do the following problems using permutations.
How many three-letter words can be made using the letters {a,b,c,d,e} if no repetitions are allowed?
A grocery store has five checkout counters, and seven clerks. How many different ways can the clerks be assigned to the counters?
A group of fifteen people who are members of an investment club wish to choose a president, and a secretary. How many different ways can this be done?
Compute the following.
9P2
6P4
8P3
7P4
In how many ways can the letters of the word CUPERTINO be arranged if each letter is used only once in each arrangement?
How many permutations of the letters of the word PROBLEM end in a vowel?
How many permutations of the letters of the word SECURITY end in a consonant?
How many permutations of the letters PRODUCT have consonants in the second and third positions?
How many three-digit numbers are there?
How many three-digit odd numbers are there?
In how many different ways can five people be seated in a row if two of them insist on sitting next to each other?
In how many different ways can five people be seated in a row if two of them insist on not sitting next to each other?
In how many ways can 3 English, 3 history, and 2 math books be set on a shelf, if the English books are set on the left, history books in the middle, and math books on the right?
In how many ways can 3 English, 3 history, and 2 math books be set on a shelf, if they are grouped by subject?
You have 5 math books and 6 history books to put on a shelf with five slots. In how many ways can you put the books on the shelf if the first two slots are to be filled with math books and the next three with history books?
You have 5 math books and 6 history books to put on a shelf with five slots. In how many ways can you put the books on the shelf if the first two slots are to be filled with the books of one subject and the next three slots are to be filled with the books of the other subject?