Chapter 3. Multiple Analysis of Variance: Part III

This chapter is published by NCPEA Press and is presented as an NCPEA/Connexions publication "print on demand book." Each chapter has been peer-reviewed, accepted, and endorsed by the National Council of Professors of Educational Administration (NCPEA) as a significant contribution to the scholarship and practice of education administration.
About the Authors
John R. Slate is a Professor at Sam Houston State University where he teaches Basic and Advanced Statistics courses, as well as professional writing, to doctoral students in Educational Leadership and Counseling. His research interests lie in the use of educational databases, both state and national, to reform school practices. To date, he has chaired and/or served over 100 doctoral student dissertation committees. Recently, Dr. Slate created a website (Writing and Statistical Help) to assist students and faculty with both statistical assistance and in editing/writing their dissertations/theses and manuscripts.
Ana Rojas-LeBouef is a Literacy Specialist at the Reading Center at Sam Houston State University where she teaches developmental reading courses. Dr. LeBoeuf recently completed her doctoral degree in Reading, where she conducted a 16-year analysis of Texas statewide data regarding the achievement gap. Her research interests lie in examining the inequities in achievement among ethnic groups. Dr. Rojas-LeBouef also assists students and faculty in their writing and statistical needs on the Writing and Statistical Help website.
Now that you are in the SPSS output screen, your screen should look like the following: Your first table is titled Between-Subjects Factors and it is entirely redundant with the table immediately below it. The column of n in the Between-Subjects Factors table is duplicated in the Descriptive Statistics table. Therefore, we will not use the Between-Subjects Factors table.
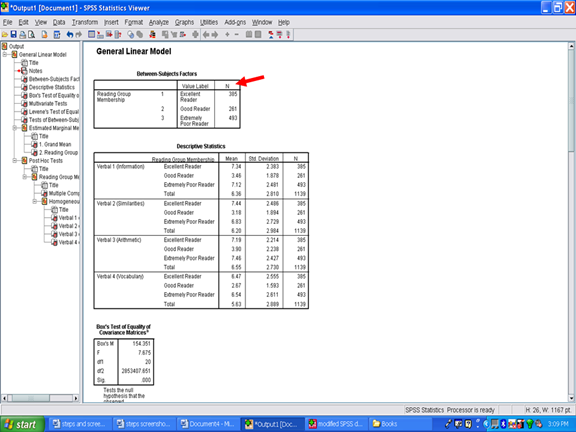
Focusing on the Descriptive Statistics table will show you a column for the M, for the SD, and for the sample size, n. This information has been provided to you for each of the four dependent variables for each of the three groups. This information will be used in your Results section and should be kept.
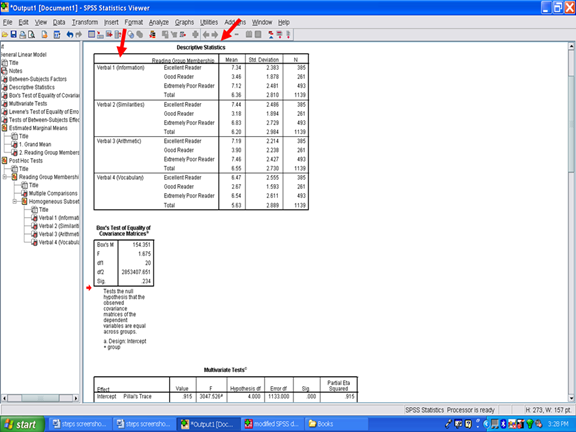
Underneath the Descriptive Statistics table is the Box’s Test of Equality of Covariance Matrices. The information in this box involves checking one of the assumptions underlying use of a MANOVA procedure. The Sig. value in this box should be greater than .05 if the assumption is met. In the example below, the Sig. value is .234 which means that this particular assumption has been met. Readers should be informed whether the Box’s M assumption was met or was violated. See Field (2010) for a detailed explanation of Box’s M and the use of a MANOVA, even when this assumption is violated.
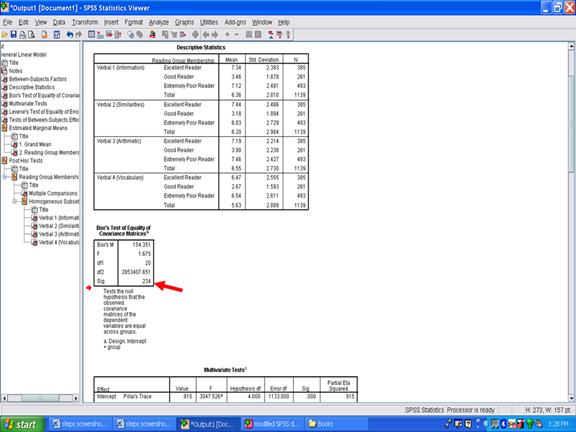
Underneath the Box’s Test of Equality of Covariance Matrices is the Multivariate Tests table. This table is important because it indicates whether or not a statistically significant difference is present among the reading groups (i.e., our independent variable) in the aggregated dependent variable (i.e., aggregated Verbal 1 through Verbal 4). For our purposes, we will use Wilks’ Lambda to determine whether or not a difference is present. In this example, a statistically significant difference is present.
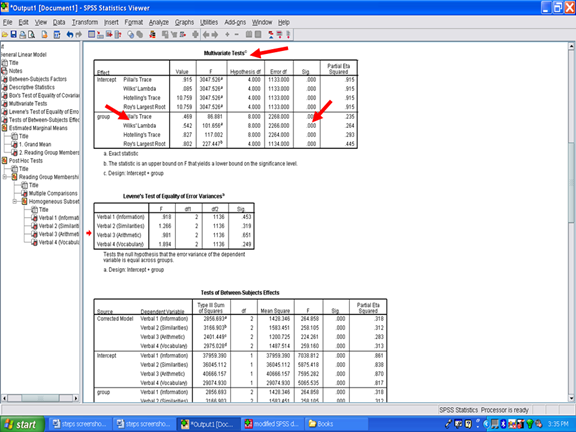
Next, the Levene’s Test of Equality of Error Variances table is examined. This table involves checking the assumption that the variability is consistent within each dependent variable for each cell in the research design. The Sig. value in each row must be greater than .05 for each assumption to be met. In the table below, the assumption of equality of error variances is met for all four dependent variables as the Sig. values range from .249 to .651. Readers should be informed that this assumption for each dependent variable was met or was not met. See Field (2010) for a detailed discussion regarding Levene’s Test and the robustness of MANOVA, even when this assumption is violated.
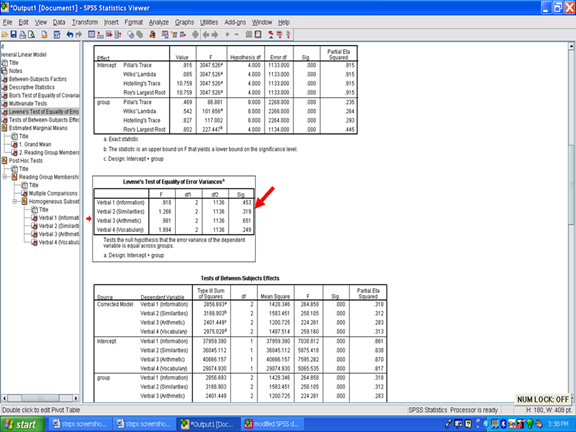
Underneath the Levene’s Test of Equality table is the Tests of Between-Subjects Effects table. Contained in this table are the univariate ANOVAs regarding whether the reading groups differ on each of the four dependent variables. The Wilks’ Lambda simply indicated whether an overall difference across the aggregated dependent variables was present. It did not provide information on whether the difference was for one, two, three, or all four of the dependent variables.
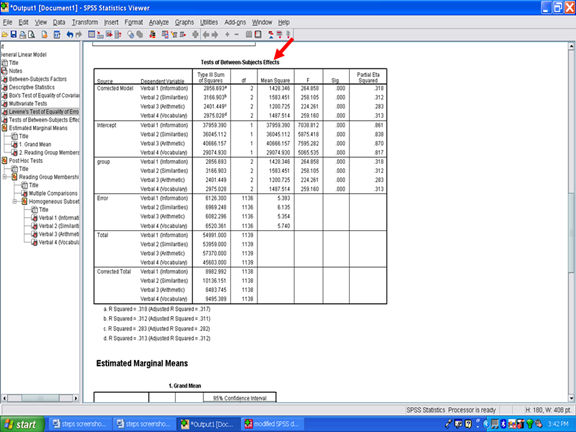
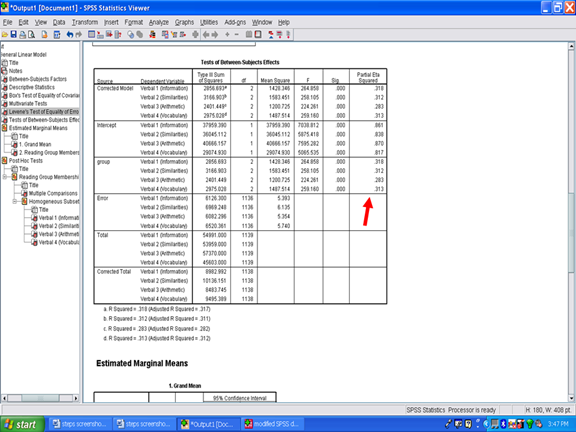
Find the row section that begins with the name of the independent variable. In our case, the independent variable is labeled group. Each row in this group section is a separate analysis of variance result. Examining the Sig. column for our four rows shows that each univariate ANOVA yielded a statistically significant result.
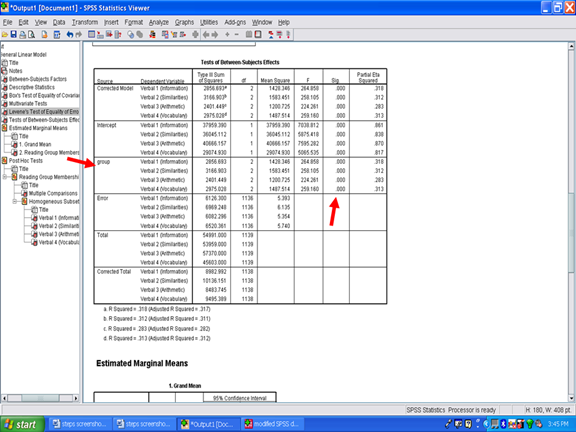
These results may be interpreted to mean that a statistically significant difference was present for Verbal 1, for Verbal 1, for Verbal 3, and for Verbal 4 as a function of the reading group. The effect size information for each statistically significant difference is present in the last column, the one labeled Partial Eta Squared. Partial eta squared, or n2, is the effect size metric provided to you in the SPSS output. To interpret whether it is small, moderate, or large, see Cohen (1988).
Because a statistically significant difference is present for each dependent variable, post hoc procedures must be examined to determine if all groups differ from each other or if only some of the groups differ. Post hoc procedure information is provided in the Multiple Comparisons table. The arrow below is pointed toward the specific type of post hoc we requested.
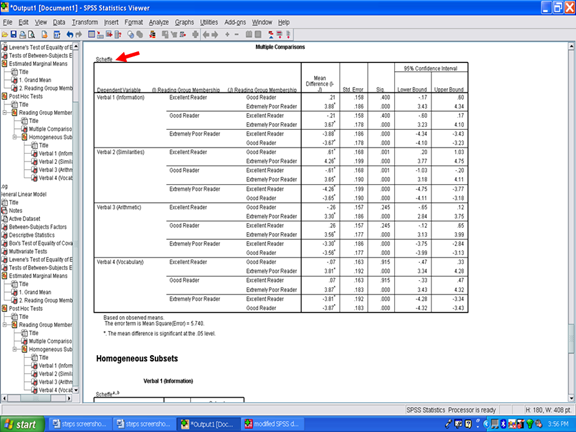
The most important column in this post hoc table is the Sig. column. For a pairwise comparison to be statistically significant, the Sig. value must be .05 or below. In the example below for the Verbal 1 set of comparisons, Excellent Readers did not differ from Good Readers, however, Excellent readers did differ from Extremely Poor Readers.
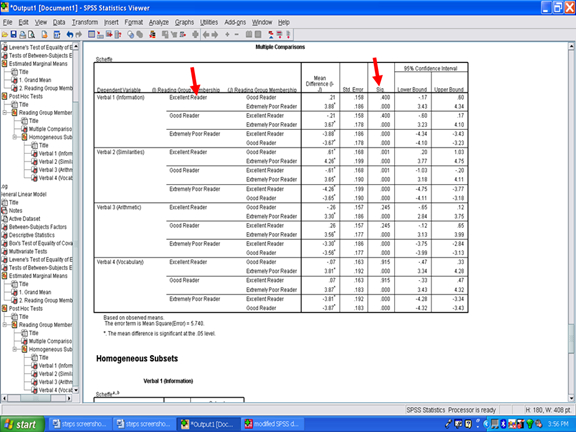
Readers should note that only three pairwise comparisons are unique in the table for each dependent variable. SPSS, however, provides information on six pairwise comparisons. When three groups are present, as they are in this example, row 1, row 2, and row 4 are unique. Row 1 is Excellent Reader compared to Good Reader. Row 2 is Excellent Reader compared to Extremely Poor Reader. Row 4 is Good Reader compared to Extremely Poor Reader.
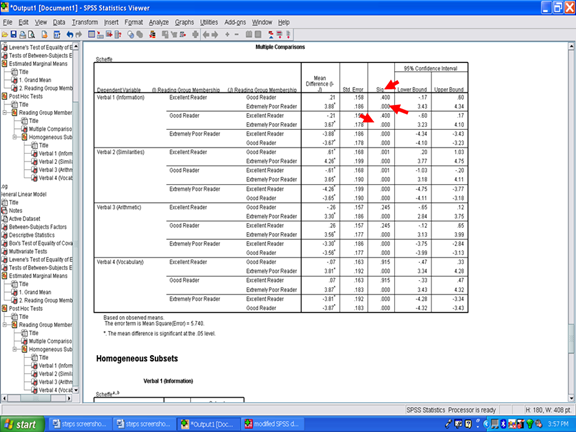
Each of the four dependent variables in this example have post hoc procedures calculated for them and are present in the table above.
All of the useful information present in the SPSS output for the MANOVA procedure has now been covered.















