Chapter 12
F Distribution and ANOVA
12.1 F Distribution and ANOVA1
12.1.1 Student Learning Objectives
By the end of this chapter, the student should be able to:
• Interpret the F probability distribution as the number of groups and the sample size change.
• Discuss two uses for the F distribution, ANOVA and the test of two variances.
• Conduct and interpret ANOVA.
• Conduct and interpret hypothesis tests of two variances (optional).
12.1.2 Introduction
Many statistical applications in psychology, social science, business administration, and the natural sciences
involve several groups. For example, an environmentalist is interested in knowing if the average amount of
pollution varies in several bodies of water. A sociologist is interested in knowing if the amount of income a
person earns varies according to his or her upbringing. A consumer looking for a new car might compare
the average gas mileage of several models.
For hypothesis tests involving more than two averages, statisticians have developed a method called Anal-
ysis of Variance" (abbreviated ANOVA). In this chapter, you will study the simplest form of ANOVA called
single factor or one-way ANOVA. You will also study the F distribution, used for ANOVA, and the test of
two variances. This is just a very brief overview of ANOVA. You will study this topic in much greater detail
in future statistics courses.
• ANOVA, as it is presented here, relies heavily on a calculator or computer.
• For further information about ANOVA, use the online link ANOVA2 . Use the back button to return
here. (The url is http://en.wikipedia.org/wiki/Analysis_of_variance.)
1This content is available online at <http://cnx.org/content/m17065/1.7/>.
2http://en.wikipedia.org/wiki/Analysis_of_variance
505
506
CHAPTER 12. F DISTRIBUTION AND ANOVA
12.2 ANOVA3
12.2.1 F Distribution and ANOVA: Purpose and Basic Assumption of ANOVA
The purpose of an ANOVA test is to determine the existence of a statistically significant difference among
several group means. The test actually uses variances to help determine if the means are equal or not.
In order to perform an ANOVA test, there are three basic assumptions to be fulfilled:
• Each population from which a sample is taken is assumed to be normal.
• Each sample is randomly selected and independent.
• The populations are assumed to have equal standard deviations (or variances).
12.2.2 The Null and Alternate Hypotheses
The null hypothesis is simply that all the group population means are the same. The alternate hypothesis
is that at least one pair of means is different. For example, if there are k groups:
Ho : µ 1 = µ 2 = µ 3 = ... = µ k
Ha : At least two of the group means µ 1, µ 2, µ 3, ..., µ k are not equal.
12.3 The F Distribution and the F Ratio4
The distribution used for the hypothesis test is a new one. It is called the F distribution, named after Sir
Ronald Fisher, an English statistician. The F statistic is a ratio (a fraction). There are two sets of degrees of
freedom; one for the numerator and one for the denominator.
For example, if F follows an F distribution and the degrees of freedom for the numerator are 4 and the
degrees of freedom for the denominator are 10, then F ∼ F4,10.
To calculate the F ratio, two estimates of the variance are made.
1. Variance between samples: An estimate of 2
σ that is the variance of the sample means. If the samples
are different sizes, the variance between samples is weighted to account for the different sample sizes.
The variance is also called variation due to treatment or explained variation.
2. Variance within samples: An estimate of 2
σ that is the average of the sample variances (also known
as a pooled variance). When the sample sizes are different, the variance within samples is weighted.
The variance is also called the variation due to error or unexplained variation.
• SSbetween = the sum of squares that represents the variation among the different samples.
• SSwithin = the sum of squares that represents the variation within samples that is due to chance.
To find a "sum of squares" means to add together squared quantities which, in some cases, may be weighted.
We used sum of squares to calculate the sample variance and the sample standard deviation in Descriptive
Statistics.
MS means "mean square." MSbetween is the variance between groups and MSwithin is the variance within
groups.
Calculation of Sum of Squares and Mean Square
3This content is available online at <http://cnx.org/content/m17068/1.6/>.
4This content is available online at <http://cnx.org/content/m17076/1.9/>.
507
• k = the number of different groups
• nj = the size of the jth group
• sj= the sum of the values in the jth group
• N = total number of all the values combined. (total sample size: ∑ nj)
• x = one value: ∑ x = ∑ sj
• Sum of squares of all values from every group combined: ∑ x2
• Between group variability: SStotal = ∑ x2 − (∑ x)2
N
• Total sum of squares: ∑ x2 − (∑ x)2
N
• Explained variation- sum of squares representing variation among the different samples SSbetween =
∑ (sj)2
(∑ s
−
j )2
nj
N
• Unexplained variation- sum of squares representing variation within samples due to chance:
SSwithin = SStotal − SSbetween
• df’s for different groups (df’s for the numerator): dfbetween = k − 1
• Equation for errors within samples (df’s for the denominator): dfwithin = N − k
• Mean square (variance estimate) explained by the different groups: MSbetween = SSbetween
dfbetween
• Mean square (variance estimate) that is due to chance (unexplained): MSwithin = SSwithin
dfwithin
MSbetween and MSwithin can be written as follows:
• MSbetween = SSbetween = SSbetween
d f between
k−1
• MSwithin = SSwithin = SSwithin
d f within
N−k
The ANOVA test depends on the fact that MSbetween can be influenced by population differences among
means of the several groups. Since MSwithin compares values of each group to its own group mean, the fact
that group means might be different does not affect MSwithin.
The null hypothesis says that all groups are samples from populations having the same normal distribution.
The alternate hypothesis says that at least two of the sample groups come from populations with different
normal distributions. If the null hypothesis is true, MSbetween and MSwithin should both estimate the same
value.
NOTE: The null hypothesis says that all the group population means are equal. The hypothesis of
equal means implies that the populations have the same normal distribution because it is assumed
that the populations are normal and that they have equal variances.
F-Ratio or F Statistic
MS
F =
between
(12.1)
MSwithin
If MSbetween and MSwithin estimate the same value (following the belief that Ho is true), then the F-ratio
should be approximately equal to 1. Only sampling errors would contribute to variations away from 1. As
it turns out, MSbetween consists of the population variance plus a variance produced from the differences
between the samples. MSwithin is an estimate of the population variance. Since variances are always pos-
itive, if the null hypothesis is false, MSbetween will be larger than MSwithin. The F-ratio will be larger than
1.
The above calculations were done with groups of different sizes. If the groups are the same size, the calcu-
lations simplify somewhat and the F ratio can be written as:
508
CHAPTER 12. F DISTRIBUTION AND ANOVA
F-Ratio Formula when the groups are the same size
n · (s_
F =
x )2
(12.2)
2
spooled
where ...
• (sx)2 =the variance of the sample means
• n =the sample size of each group
2
•
spooled
=the mean of the sample variances (pooled variance)
• dfnumerator = k − 1
• dfdenominator = k (n − 1) = N − k
The ANOVA hypothesis test is always right-tailed because larger F-values are way out in the right tail of
the F-distribution curve and tend to make us reject Ho.
12.3.1 Notation
The notation for the F distribution is F ∼ Fdf(num),df(denom)
where df(num) = d f between and df(denom) = d f within
The mean for the F distribution is µ =
d f (num)
d f (denom)−1
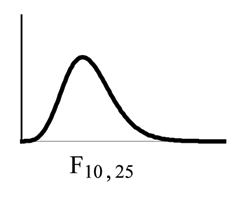
12.4 Facts About the F Distribution5
1. The curve is not symmetrical but skewed to the right.
2. There is a different curve for each set of dfs.
3. The F statistic is greater than or equal to zero.
4. As the degrees of freedom for the numerator and for the denominator get larger, the curve approxi-
mates the normal.
5. Other uses for the F distribution include comparing two variances and Two-Way Analysis of Variance.
Comparing two variances is discussed at the end of the chapter. Two-Way Analysis is mentioned for
your information only.
5This content is available online at <http://cnx.org/content/m17062/1.11/>.

509
(a)
(b)
Figure 12.1
Example 12.1
One-Way ANOVA: Four sororities took a random sample of sisters regarding their grade averages
for the past term. The results are shown below:
GRADE AVERAGES FOR FOUR SORORITIES
Sorority 1
Sorority 2
Sorority 3
Sorority 4
2.17
2.63
2.63
3.79
1.85
1.77
3.78
3.45
2.83
3.25
4.00
3.08
1.69
1.86
2.55
2.26
3.33
2.21
2.45
3.18
Table 12.1
Problem
Using a significance level of 1%, is there a difference in grade averages among the sororities?
Solution
Let µ 1, µ 2, µ 3, µ 4 be the population means of the sororities. Remember that the null hypothesis
claims that the sorority groups are from the same normal distribution. The alternate hypothesis
says that at least two of the sorority groups come from populations with different normal distri-
butions. Notice that the four sample sizes are each size 5.
Ho : µ 1 = µ 2 = µ 3 = µ 4
Ha: Not all of the means µ 1, µ 2, µ 3, µ 4 are equal.
Distribution for the test: F3,16
where k = 4 groups and N = 20 samples in total
d f (num) = k − 1 = 4 − 1 = 3
510
CHAPTER 12. F DISTRIBUTION AND ANOVA
d f (denom) = N − k = 20 − 4 = 16
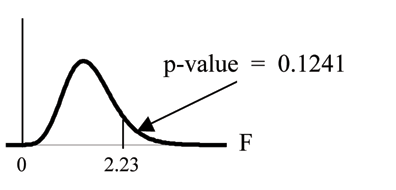
Calculate the test statistic: F = 2.23
Graph:
Figure 12.2
Probability statement: p-value = P (F > 2.23) = 0.1241
Compare α and the p − value: α = 0.01
p-value = 0.1242
α < p-value
Make a decision: Since α < p-value, you cannot reject Ho.
This means that the population averages appear to be the same.
Conclusion: There is not sufficient evidence to conclude that there is a difference among the grade
averages for the sororities.
TI-83+ or TI 84: Put the data into lists L1, L2, L3, and L4. Press ❙❚❆❚ and arrow over to ❚❊❙❚❙.
Arrow down to ❋✿❆◆❖❱❆. Press ❊◆❚❊❘ and Enter (▲✶✱▲✷✱▲✸✱▲✹). The F statistic is 2.2303 and the
p-value is 0.1241. df(numerator) = 3 (under ✧❋❛❝t♦r✧) and df(denominator) = 16 (under ❊rr♦r).
Example 12.2
A fourth grade class is studying the environment. One of the assignments is to grow bean plants
in different soils. Tommy chose to grow his bean plants in soil found outside his classroom mixed
with dryer lint. Tara chose to grow her bean plants in potting soil bought at the local nursery.
Nick chose to grow his bean plants in soil from his mother’s garden. No chemicals were used
on the plants, only water. They were grown inside the classroom next to a large window. Each
child grew 5 plants. At the end of the growing period, each plant was measured, producing the
following data (in inches):
511
Tommy’s Plants
Tara’s Plants
Nick’s Plants
24
25
23
21
31
27
23
23
22
30
20
30
23
28
20
Table 12.2
Problem 1
Does it appear that the three media in which the bean plants were grown produce the same
average height? Test at a 3% level of significance.
Solution
This time, we will perform the calculations that lead to the F’ statistic. Notice that each group has
the same number of plants so we will use the formula F’ = n·(s_x)2 .
(spooled)2
First, calculate the sample mean and sample variance of each group.
Tommy’s Plants
Tara’s Plants
Nick’s Plants
Sample Mean
24.2
25.4
24.4
Sample Variance
11.7
18.3
16.3
Table 12.3
Next, calculate the variance of the three group means (Calculate the variance of 24.2, 25.4, and
24.4). Variance of the group means = 0.413 = (sx)2
Then MSbetween = n (sx)2 = (5) (0.413) where n = 5 is the sample size (number of plants each
child grew).
Calculate the average of the three sample variances (Calculate the average of 11.7, 18.3, and 16.3).
2
Average of the sample variances = 15.433 = spooled
2
Then MSwithin = spooled
= 15.433.
The F statistic (or F ratio) is F = MSbetween = n·(s_x)2 = (5)·(0.413) = 0.134
MSwithin
(s
15.433
pooled )2
The dfs for the numerator = the number of groups − 1 = 3 − 1 = 2
The dfs for the denominator = the total number of samples − the number of groups = 15 − 3 = 12
The distribution for the test is F2,12 and the F statistic is F = 0.134
The p-value is P (F > 0.134) = 0.8759.
512
CHAPTER 12. F DISTRIBUTION AND ANOVA
Decision: Since α = 0.03 and the p-value = 0.8759, do not reject Ho. (Why?)
Conclusion: With a 3% the level of significance, from the sample data, the evidence is not sufficient
to conclude that the average heights of the bean plants are not different. Of the three media tested,
it appears that it does not matter which one the bean plants are grown in.
(This experiment was actually done by three classmates of the son of one of the authors.)
Another fourth grader also grew bean plants but this time in a jelly-like mass. The heights were
(in inches) 24, 28, 25, 30, and 32.
Problem 2
(Solution on p. 524.)
Do an ANOVA test on the 4 groups. You may use your calculator or computer to perform the
test. Are the heights of the bean plants different? Use a solution sheet (Section 13.5.4).
12.4.1 Optional Classroom Activity
Randomly divide the class into four groups of the same size. Have each member of each group record the
number of states in the United States he or she has visited. Run an ANOVA test to determine if the average
number of states visited in the four groups are the same. Test at a 1% level of significance. Use one of the
solution sheets (Section 13.5.4) at the end of the chapter (after the homework).
513
12.5 Summary6
• An ANOVA hypothesis test determines if several population means are equal. The distribution for
the test is the F distribution with 2 different degrees of freedom.
Assumptions:
a. Each population from which a sample is taken is assumed to be normal.
b. Each sample is randomly selected and independent.
c. The populations are assumed to have equal standard deviations (or variances)
• A Test of Two Variances hypothesis test determines if two variances are the same. The distribution
for the hypothesis test is the F distribution with 2 different degrees of freedom.
Assumptions:
a. The populations from which the two samples are drawn are normally distributed.
b. The two populations are independent of each other.
6This content is available online at <http://cnx.org/content/m17072/1.3/>.
514
CHAPTER 12. F DISTRIBUTION AND ANOVA
12.6 Practice: ANOVA7
12.6.1 Student Learning Outcome
• The student will explore the properties of ANOVA.
12.6.2 Given
Suppose a group is interested in determining whether teenagers obtain their drivers licenses at approxi-
mately the same average age across the country. Suppose that the following data are randomly collected
from five teenagers in each region of the country. The numbers represent the age at which teenagers ob-
tained their drivers licenses.
Northeast
South
West
Central
East
16.3
16.9
16.4
16.2
17.1
16.1
16.5
16.5
16.6
17.2
16.4
16.4
16.6
16.5
16.6
16.5
16.2
16.1
16.4
16.8
x =
________
________
________
________
________
s2 =
________
________
________
________
________
Table 12.4
12.6.3 Hypothesis
Exercise 12.6.1
State the hypotheses.
Ho:
Ha:
12.6.4 Data Entry
Enter the data into your calculator or computer.
Exercise 12.6.2
(Solution on p. 524.)
degrees of freedom - numerator: df (n) =
Exercise 12.6.3
(Solution on p. 524.)
degrees of freedom - denominator: df (d) =
Exercise 12.6.4
(Solution on p. 524.)
F test statistic =
Exercise 12.6.5
(Solution on p. 524.)
p-value =
7This content is available online at <http://cnx.org/content/m17067/1.8/>.
515
12.6.5 Decisions and Conclusions
State the decisions and conclusions (in complete sentences) for the following preconceived levels of α .
Exercise 12.6.6
α = 0.05
Decision:
Conclusion:
Exercise 12.6.7
α = 0.01
Decision:
Conclusion:
516
CHAPTER 12. F DISTRIBUTION AND ANOVA
12.7 Homework8
DIRECTIONS: Use a solution sheet to conduct the following hypothesis tests. The solution sheet
can be found in the Table of Contents 14. Appendix.
Exercise 12.7.1
(Solution on p. 524.)
Three students, Linda, Tuan, and Javier, are given 5 laboratory rats each for a nutritional experi-
ment. Each rat’s weight is recorded in grams. Linda feeds her rats Formula A, Tuan feeds his rats
Formula B, and Javier feeds his rats Formula C. At the end of a specified time period, each rat is
weighed again and the net gain in grams is recorded. Using a significance level of 10%, test the
hypothesis that the three formulas produce the same average weight gain.
Weights of Student Lab Rats
Linda’s rats
Tuan’s rats
Javier’s rats
43.5
47.0
51.2
39.4
40.5
40.9
41.3
38.9
37.9
46.0
46.3
45.0
38.2
44.2
48.6
Table 12.5
Exercise 12.7.2
A grassroots group opposed to a proposed increase in the gas tax claimed that the increase
would hurt working-class people the most, since they commute the farthest to work. Suppose
that the group randomly surveyed 24 individuals and asked them their daily one-way commut-
ing mileage. The results are below:
working-class
professional (middle incomes)
professional (wealthy)
17.8
16.5
8.5
26.7
17.4
6.3
49.4
22.0
4.6
9.4
7.4
12.6
65.4
9.4
11.0
47.1
2.1
28.6
19.5
6.4
15.4
51.2
13.9
9.3
Table 12.6
Exercise






